1. 베이즈 정리 (Bayes' Theorem)
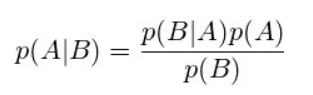
p(A): 사전 확률
p(B|A): 우도(likelihood)
p(B): B의 사전 확률
p(A|B): A의 사후 확률
베이즈 정리는 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리이다. 사전확률로 부터 사후확률을 구할 수 있다.
-조건부 확률
-분자만 비교하기
2. 나이브 베이즈 종류 및 이해
-설명변수가 연속형 변수일 때, Gaussian Naive Bayes (가우시안 나이브 베이즈)
-설명변수가 범주형 변수일 때, Multinomial Naive Bayes (다항 나이브 베이즈)
-범주형 변수일 때, 범주가 2개인 이진형일 경우, Bernoulli naive Bayes (베르누이 나이브 베이즈)
1) Gaussian Naive Bayes
표본 평균과 표본 분산을 가진 정규분포 하에서 베이즈 정리 사용한 것이다.
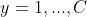
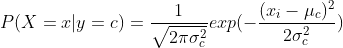
y의 범주가 정해져 있을 때, y=c에서 X=x의 정규분포의 표현식은 위와 같다.
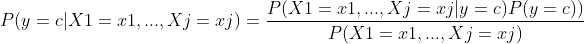
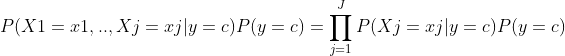
이를 조건부 독립으로 표현하고, 분류 모델의 선택 편의를 위해 분자만 비교한다. (분모는 항상 같은 조건을 나타내기 때문에)
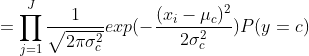
조건부 독립에 정규분포를 대입하면 위와 같다.
즉 가우시안 베이즈 정리는 정규분포를 가정한 표본들을 대상으로 독립을 나타내어, 확률이 가장 높은 경우를 선택하는 것이다. (같은 분모, 분자의 값이 큰 경우 선택)
2) Multinomial Naive Bayes


y와 k의 범주가 정해져 있을 때, y=c인 상황에서 Xk=xk일 조건부 확률은 각각의 출현횟수를 더한 팩토리얼/각각의 출현횟수를 모두 곱한 것
3) Bernoulli naive bayes
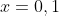
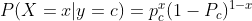
범주가 2개인 이진형인 경우, 출현할 확률은 쪼개어 질 수 있으며 조건부 확률은 다항분포로 표시할 수 있다.
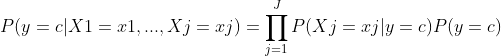
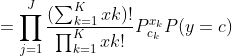
분모는 항상 동일한 조건을 가지므로 분자를 비교하고, 다항분포를 사용해 범주형 조건부 확률을 구할 수 있다.
