Boostrapping

학습 샘플을 Z라고 할 때, Z로부터 중복을 허용하여 N개의 샘플을 반복적으로 뽑는다.
샘플의 각 세트에대해 통계적 파라미터를 추정.
각 분류기의 성능을 평가.

---

Bagging

• For i=1~B:
  • Z에서 중복 허용해 N개의 샘플을 뽑음.
  • 분류기 $C_i$를 학습

이 부분 까지는 Boostrapping.

$C_1 ... C_B$까지의 결과들의 voting을 통해 최종 분류기를 구성.

-> 이 방식은 분류기의 안정성을 높이고 분산을 낮춤.

---

Boosting

• Z로 부터 중복없이 N개의 샘플을 선택 => 이 샘플을 가지고 약한 분류기 $C_1$ 학습
• Z로 부터 N개의 샘플을 선택하는데 이중 절반은 $C_1$이 잘못 분류한것으로 구성 => $C_2$ 학습
• $C_1$와 $C_2$의 결과가 다른 샘플들을 선택 => $C_3$ 학습
• 최종 분류기는 약한 분류기들의 결과로 voting하여 최종결과를 냄.

---

AdaBoost

Adaptive Boosting

• sampling 대신 re-weight
• 간단한 hypothesis는 완벽하지 않기 때문에, hypothesis들의 결합

Discrete AdaBoost - Freund & Shapire, 1996

입력: N개의 라벨링된 샘플 ${(x_1, y_1),...,(x_N,y_N)}, y_i\in \{-1,1\}$
초기화: weight 초기화 ($w_i^1=\frac{1}{N}$)
(i번째 데이터, t번째 약한 분류기)

for t=1 to T do
	1. weakClassifer를 얻음.
    2. alpha 계산.
    3. weight 업데이트.
endfor

Output strong Classifier

Psedocode를 자세히 살펴보면 다음과 같다.

1. weakClassifier 선택

에러 $e_t$가 작은 약한 분류기를 선택한다. $h_t$는 약한 분류기의 예측값이다.

만약 약한분류기가 정답을 모두 맞췄다면, $y_ih_t$는 1이 될 것이고,
정답을 모두 틀렸다면, $y_ih_t$는 -1이 될 것이다.

weight를 모두 더한 $\sum w$는 1이므로,
정답을 모두 맞춘 약한 분류기의 에러는 0이고, 모두 틀린 분류기의 에러는 1이 된다.

2. $\alpha_t$ 계산

정의에 의해 $e_t$가 커지면 $\alpha_t$는 작아지고 $e_t$가 작아지면 $\alpha_t$는 커진다.

3. weight 업데이트

다음 iteration에 사용될 가중치가 위의 식으로 업데이트되는데, $-\alpha_ty_ih_i(x_i)$를 보면,

분류기가 정답을 많이 맞추면 $\alpha_t$가 커지기 때문에 틀린 데이터에 대해 가중치를 높게 준다는 것을 알 수 있다.

Strong Classifier

최종적으로 T번째 약한 분류기까지 학습을 했으면 약한분류기들을 가지고 강한 분류기를 만들어 최종 예측값을 내놓게 된다.

Weak Classifier

약한 분류기는 데이터를 잘 분류하는 threshold 하나를 정하게 된다.
다음과 같은 2차원 데이터가 있다고 해보자.

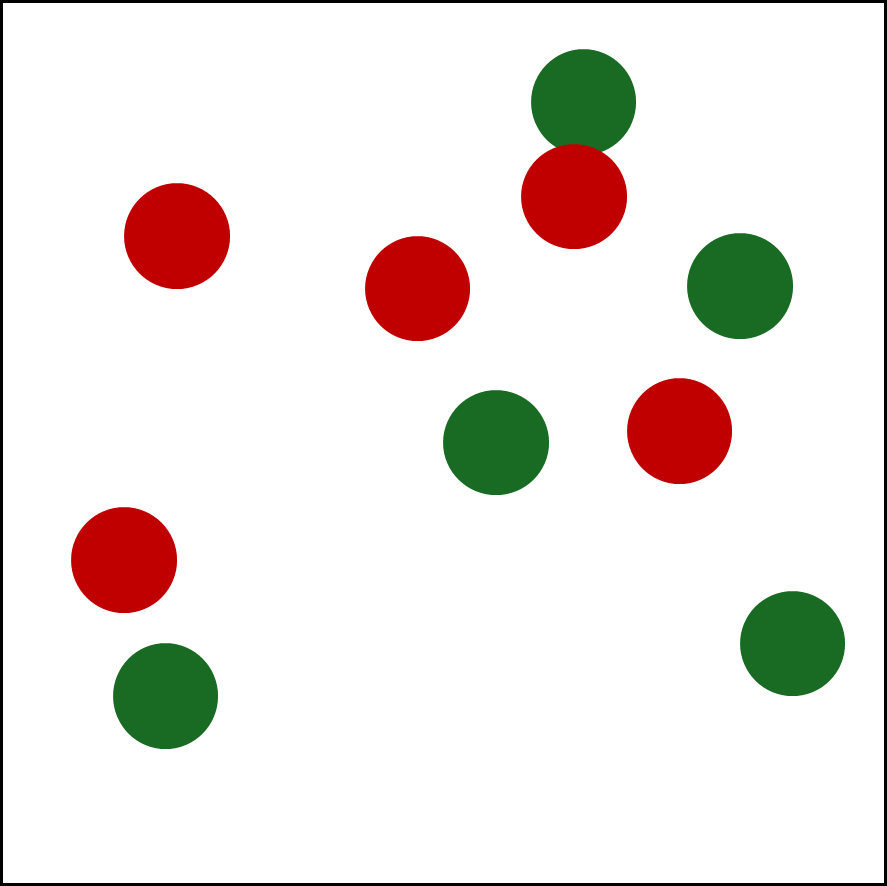
초록색이 positive, 빨간색이 negative 데이터다.

이런 데이터를 X축에 대해 다음과 같이 threshold가 정해졌다고 하면,

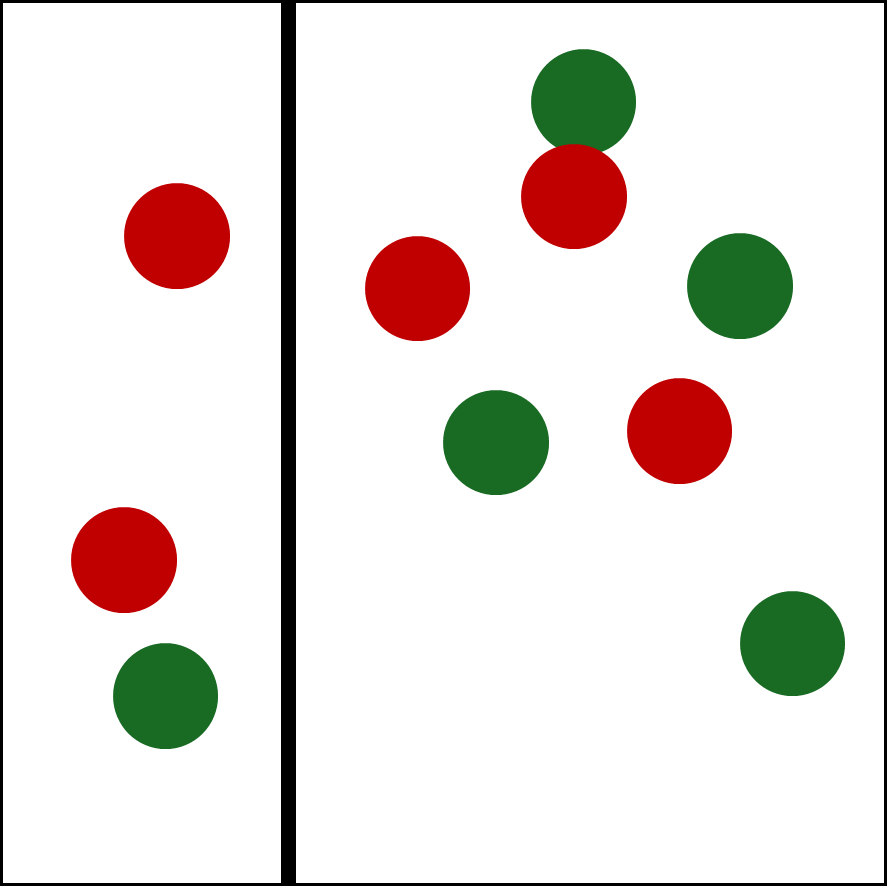
threshold를 기준으로 왼쪽을 positive로 분류할 수도, 오른쪽을 positive로 분류할 수도 있다.

• polarity를 고려해야할 필요가 있다.

• 정확도를 사용한다.
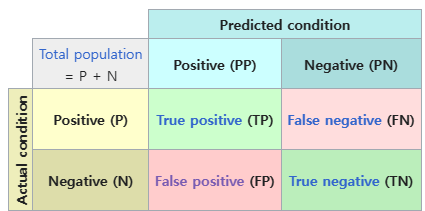  wiki-confusion_matrix

그렇다면 Threshold는 어떻게 정해질까?

Optimal Threshold

약한 분류기에서 최적의 Threshold를 정할때는 feature에 대한 누적합을 사용한다.

for i=1 to (number of features) N do
	1. i번째 feature에 대해 데이터를 sorting
    2. positive 샘플과 negative 샘플의 누적합을 계산한다
    3. threshold와 polarity를 찾는다.
endfor

반복문의 한 iteration을 살펴보자.

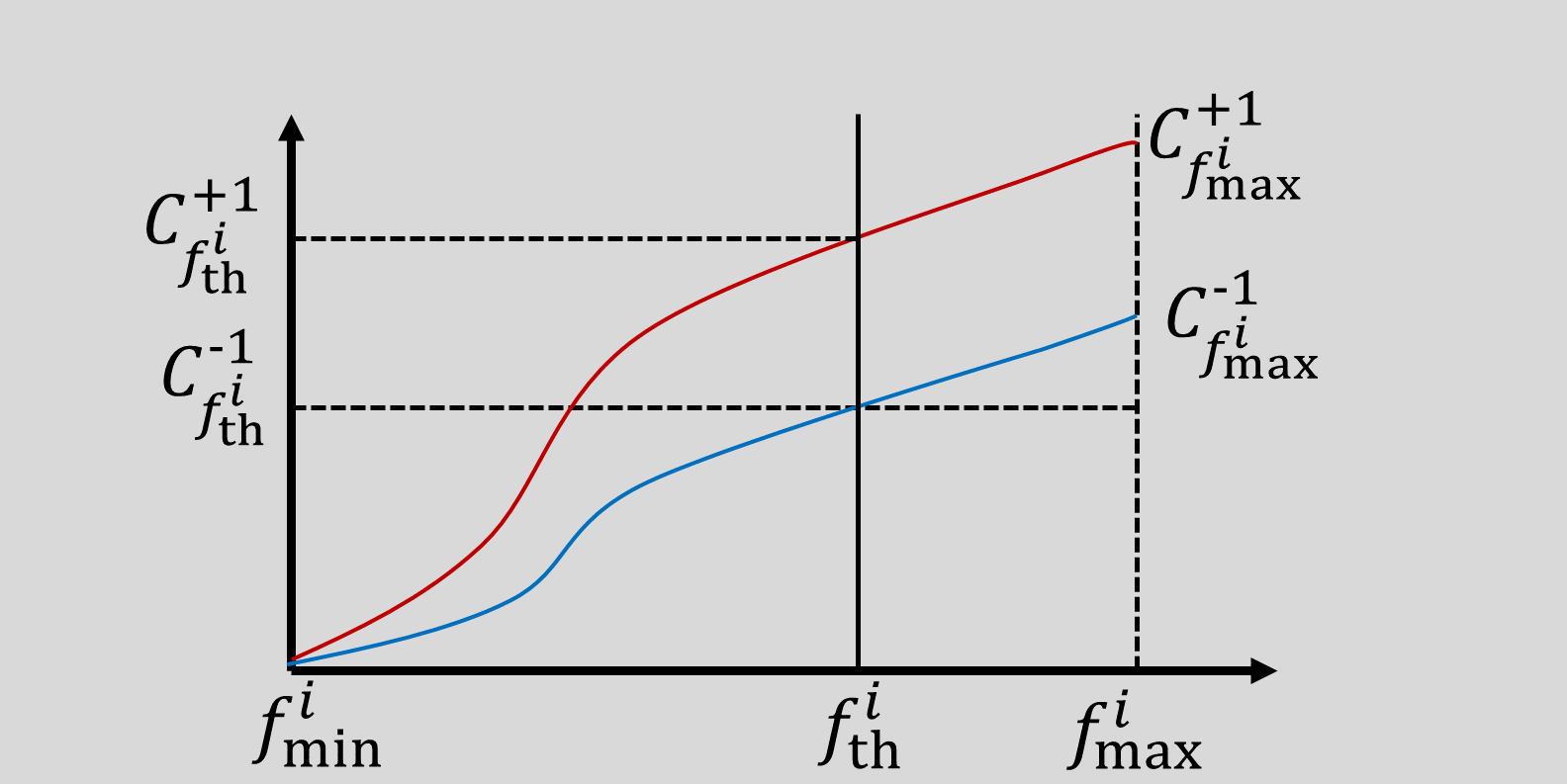
i번째 feature에 대해 위 와 같이 positive/negative 샘플의 누적합이 구해졌을때

Threshold를 임의로 정해보면, 누적합으로 부터 해당 threshold를 분류기의 threshold로 정했을때의 FN, FP를 구할 수 있다.

if $p=1$ at $f_{th}$
  FN = $C^{+1}_{f_{th}}$
  FP = $C^{-1}_{f_{max}}-C^{-1}_{f_{th}}$
  $Sum^{+1}_{th}=C^{+1}_{f_{th}}+C^{-1}_{f_{max}}-C^{-1}_{f_{th}}$

$p=1$ 일 때, threshold 오른쪽은 positive, 왼쪽은 negative로 분류하므로, FN(실제:p, 분류기: n)은 $C^{+1}_{f_{th}}$이 되고, FP(실제: n, 분류기: p)는 $C^{-1}_{f_{max}}-C^{-1}_{f_{th}}$가 된다.

if $p=-1$ at $f_{th}$
  FN = $C^{+1}_{f_{max}}-C^{+1}_{f_{th}}$
  FP = $C^{-1}_{f_{th}}$
  $Sum^{-1}_{th}=C^{-1}_{f_{th}}+C^{+1}_{f_{max}}-C^{+1}_{f_{th}}$

$p=-1$ 일 때는 반대이다.

$Sum_{f_{th}}=min(Sum^{+1}_{th}, Sum^{-1}_{th})$
$p_{th}=argmin_p(Sum^p_{f_{th}})$
$f_{th}=argmin(Sum_{f_{th}})$

최종적으로, polarity는 1과 -1 중 FP+FN를 작게 만드는 값으로 결정되고, threshold는 polarity가 정해질때 만들어진 FP+FN이 최소가 되는 지점이 된다.

$h_t(x_i)$

모든 feature에 대해 threshold와 polarity가 정해졌다면 약한 분류기를 구성할 수 있게 된다.

여기서 n은 feature의 번호이다.

따라서 error가 가장 작은 feature, threshold, polarity를 찾으면 최종적으로 $h_t(x_i)$를 찾은것이다.