Viola-Jones Algorithm 특징

• 얼굴 분류
• feature를 추출
• 병렬 구조의 학습기
• scaling

---

Haar-like feature

학습을 할때 24x24 서브 윈도우 이미지가 들어오면 haar-like feature로 feature를 생성하게 된다.

Haar-like feature에는 4가지의 기본 커널이 있는데, kernel value(1x1), two-rectangle type, three-rectangle type, four-rectangle type 이다.

위의 이미지에서 커널의 흰 부분이 -1, 어두운 부분이 1인 커널이어서 어두운 부분의 합에서 흰 부분의 합을 빼면 해당 피처의 데이터가 된다.

feature의 수

각 커널은 기본 크기에서 x축 방향의 크기의 배수, y축 방향의 크기의 배수만큼 씩 키울 수 있다. 최대로 키울 수 있는 크기는 sub-window의 크기가 24x24이므로 각 방향에서 24까지 이다.

two-rectangle type

기본 커널의 크기는 1x2 이다.

x축 방향으로는 $2, 4, 6, \dots ,24$ 까지 2의 배수씩 키울 수 있고,
y축 방향으로는 $1, 2, 3, \dots ,24$ 까지 1씩 늘리며 키울 수 있다.

x축 방향으로 커널이 움직일 수 있는 횟수는 $size_{window} -size_x + 1$로 계산할 수 있고, 가능한 사이즈에 대해 계산하면 다음과 같이 계산할 수 있다.

y축 방향으로 커널이 움직일 수 있는 횟수는 다음과 같다.

세로로 되어있는 기본커널의 크기는 2x1이고 이때도 위와 같이 계산할 수 있다.

따라서 two-rectangle type으로 만들수 있는 feature의 수는 $144\times300\times2=86,400$ 개.

three-rectangle type

위와 동일하게 계산한다.

three-rectangle type으로 만들수 있는 feature의 수는 $92\times300\times2=55,200$

four-rectangle type

four-rectangle type은 한 가지이다.

four-rectangle type으로 만들수 있는 feature의 수는 $144\times144=20,736$

Haar-like feature로 만들어지는 총 feature의 수는 $86,400+55,200+20,736=162,336$개.

---

Integral Images

Haar-like feature를 통해 feature 추출을 하기 위해서는 이미지에서 커널에 해당하는 부분의 합을 구해야하는데 약 16만개의 feature를 추출할 때마다 영역속의 픽셀값을 더하면 연산 시간이 오래걸린다.

이런 문제 때문에 Integral Image를 만든다. Integral Image에서는 한 영역 속의 픽셀 합을 구하고 싶을 때 4개의 수의 합연산만 진행하면 된다.

Integral Image 생성

1. x축을 따라 이미지의 누적합을 계산.
2. 1의 결과 이미지에서 y축을 따라 이미지의 누적합을 계산

2	1	8
3	5	3
8	5	2

위와 같은 3x3의 이미지는

1. x축을 따라 누적합 계산

   2	3	11
   3	8	11
   8	13	15

2. 축을 따라 누적합 계산

   2	3	11
   5	11	22
   13	24	37

이렇게 Integral Image가 만들어진다.

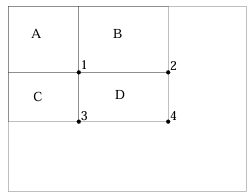
위와 같은 Integral Image가 있을 때 영역 D안의 픽셀 합은 $4-3-2+1$ 로 간단하게 계산할 수 있다.

영역 D의 좌상단 좌표를 (L, T), 우하단 좌표를 (R,B)라고 하고, 픽셀 좌표로 접근한다고 하면 다음과 같이 계산할 수 있다.

($OI$: Original Image, $II$: Integral Image)