이준석 교수님의 유튜브 강의 Lec4 Neural Network and Back Propagation 영상을 참고해서 정리한 내용입니다. 다른 출처표기가 없는 이미지는 유튜브 영상에서 가져온 것임을 밝힙니다.
https://www.youtube.com/watch?v=KDmT15zv0Rc
Neural Network
뉴럴 네트워크를 배울 때 가장 먼저 나오는 개념인 퍼셉트론부터 하나 하나 알아보자. 참고로 이미 아는 내용이 많이 나오기 때문에 이번 포스팅에서는 강의를 들으며 추가로 알면 좋을만한 팀들이나 까먹은 중요 개념들을 위주로 적었다. 따라서 처음 공부하는 사람에게는 그낙 좋은 포스팅은 아닐 것이다..😂
Perceptron
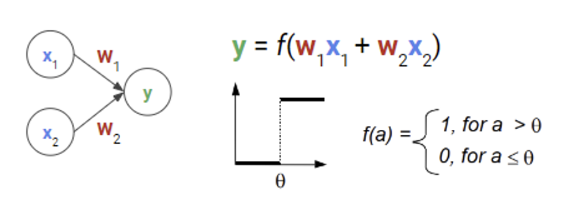
퍼셈트론은 input 값이 들어왔을 때(여기서는 1 아님 0), 각각의 인풋에 가중치 w을 곱하고 더한 값이 특정 threshold 값 이상이면 1, 이하면 0을 출력하는 논리 연산이다. 더 이상의 특별한 것은 없다.
그런데 신기한 것은 이 퍼셉트론을 이용해서 AND, OR, NOT 게이트를 만들 수 있다는 것이다. 예를 들어 threshold = 0.5일 때 w1와 w2를 잘 조절해서(e.g. 0.4, 0.2) AND 게이트를 만들 수 있다. 예를 들어 x1에는 1, x2에는 0이 있을 때 가중치와 곱해서 더하면 0.4가 된다. 이는 threshold 값 이하이므로 해당 입력은 AND가 아님을 의미한다.
하지만 NOR은 퍼셉트론 1개로 표현이 불가능하며 최소 2개가 필요함이 밝혀졌고, 이에 따라 multi layer perceptron으로 모든 식을 나타낼 수 있음을 증명해냈다.
-> 이 때문에 몇 년간 인공지능이 완전 침체기였다고 한다... 가장 간단한 논리연산 중 하나인 NOR도 못푸는데 어떻게 인공지능이라 부를 수 있는가 하며 온갖 비난을 받았다.
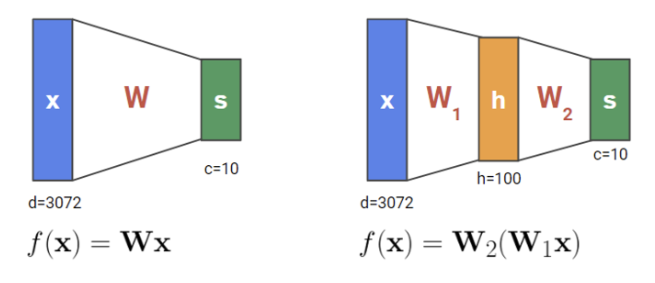
근데 이 두 그림을 보자. 왼쪽은 우리가 처음 공부했던 linear function으로, x에 W를 곱해 output을 내는 수식이다. 오른쪽은 방금 공부했던 것으로 퍼셉트론이 한 개만 있을 때의 문제점을 극복하기 위해 두 단계로 나눈 것이다.
하지만 여기엔 모순이 있다. 오른쪽 수식은 사실상 로 표현할 수 있으며 결국 두 식은 수학적으로 동일한 식이 되어버린다. 방금까지는 층이 하나라면 NOR 문제도 풀지 못한다고 했는데… 그럼 뭐가 달라진걸까?
사실 여기에는 한 가지 간과하고 있는 점이 있는데 바로 Activation function 이다.
Linear layer을 여러개 쌓아도 사실상 여전히 Linear하기 때문에 우린 사이사이에 Non-linear function 을 곱해주어 더 복잡한 데이터 패턴을 학습하게끔 한다.
Back Propagation
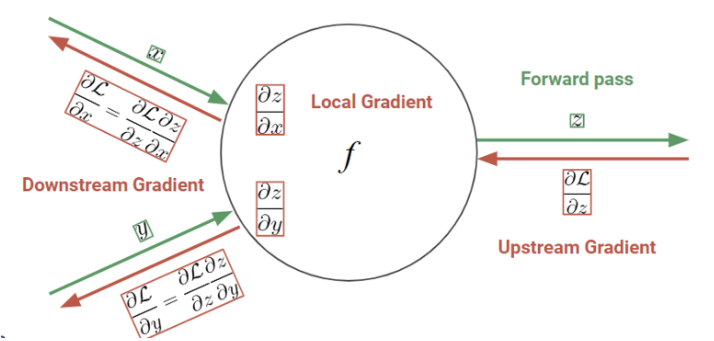
Back propagation은 로스 함수 미분을 자동화해주는 매커니즘으로 chain rule을 이용하여 그래디언트 값을 계산한다.
이번에는 input x나 output y가 스칼라 값이 아니라 벡터라면?
스칼라를 벡터로 그래디언트를 구한다면 그래디언트는 벡터의 크기만큼 나온다. 왜냐하면 벡터의 요소마다 다 그래디언트를 구해야 하기 때문. 그렇다면 벡터를 벡터로 그래디언트를 구하면 이번엔 그래디언트가 행렬로 나올 것이다. 이렇게 스칼라가 아니라 벡터인 경우에는 각 요소가 얼마나 영향을 미치는지 계산하는 것이므로 크기가 달라진 다는 것을 유의하자.
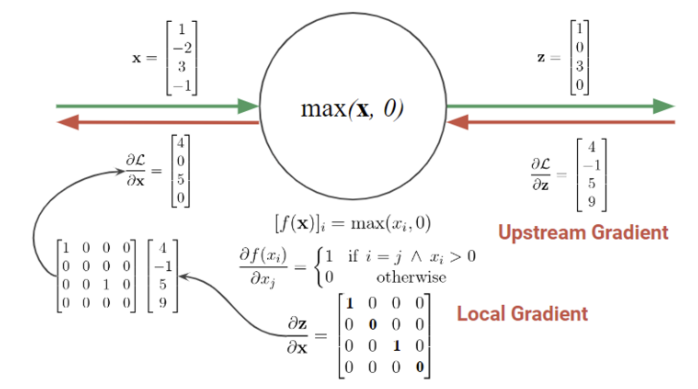
z 벡터 크기가 4이므로 그래디언트도 동일하게 길이 4가 된다.
여기서 Local gradient 를 구하기 위해선 f를 미분해야 하고, f가 max 함수이므로 미분하면 1 또는 0의 값을 갖게 된다. 이때 1을 가질 조건은 x 원소가 0보다 커야 하면서 i=j를 만족해야 한다. 그럼 그래디언트는 4x4 행렬이 되고 x값을 넣으면 위와 같은 행렬 완성!
여기서 얻어가야 하는 것은 모든 엣지에서의 변수(?) 크기와 그래디언트 크기는 동일하다는 점! 인풋이 4x4면 해당 엣지에서 그래디언트는 4x4, 아웃풋이 5x5x6이면 그래디언트도 5x5x6이 된다는 것. 별거 아닌 당연한 이야기처럼 들리지만 나중에 실제 코딩을 할 때 디버딩하는 용도로 알아두면 편하고 좋다.
오늘은 Neural Network와 back propagation 연산하는 방식에 대해 정리해보았다. 후속 포스팅은 드디어 Conv의 내용을 하나씩 다루도록 하겠다.
