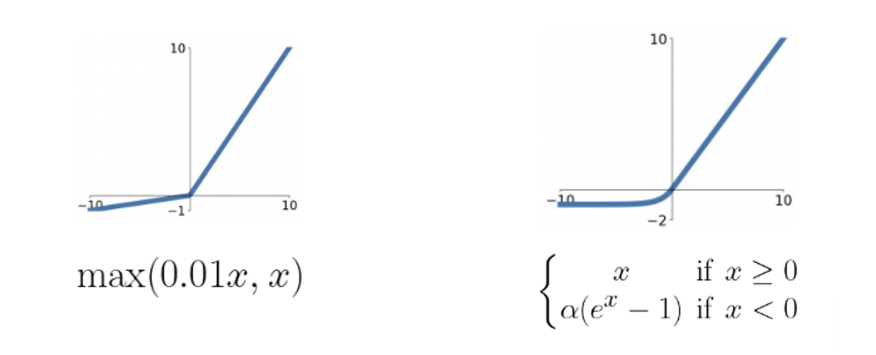
이준석 교수님의 유튜브 강의 Lec 6. Training Neural Networks I 영상을 참고해서 정리한 내용입니다. 다른 출처표기가 없는 이미지는 유튜브 영상에서 가져온 것임을 밝힙니다.
이전 포스팅에서 Loss function과 Back propagate에 대해 공부했다. 교수님 강의 lec5는 CNN에 대해 기초적인 내용을 다루시고 계신데, 거긴 패스하고 이번에는 Neural Network를 학습시키는 그 첫 번째 단계에 대해 정리해보도록 하겠다.
이제 모델을 바로 학습시키면 될 줄 알았으나 아직 갈 길이 멀다. 모델이 어떻게 돌아가는지 전반적인 흐름을 알고 코딩하려고 보면 막히는 부분들이 많이 생길텐데 바로 위에 네모친 부분들일 것이다. 이번 포스팅과 다음 포스팅에 걸쳐서 하나 하나 어떤 식으로 구축해야 하는지 알아보자.
우선 그 첫 번째로 어떻게 보면 모델 학습의 가장 중요한 역할을 하는 Activation Function 을 알아보자.
Activation Function
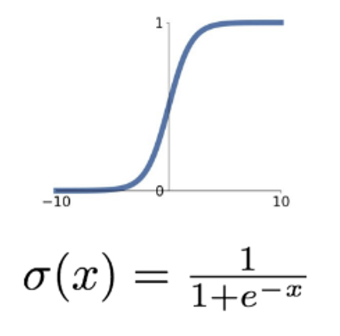
1. Sigmoid Function
역사적으로 가장 많이 사용되었던 sigmoid 함수. 장점으로는 입력 값에 대해 모두 [0, 1] 사이 값으로 매핑해주다보니 확률적으로 해석하기 용이하다는 점이 있다.
하지만 요즘에 와서는 이 sigmoid함수를 activation 함수로 쓰는 일이 매우 드물다. 그 이유는 이 sigmoid 함수에는 치명적인 단점이 있기 때문.
우선 가장 큰 문제는 입력값이 특정 범위를 벗어나면 바로 기울기가 0 이 된다. 이게 문제가 되는 이유는 바로 Activation layer에서 local gradient 가 무조건 0이 되기 때문이다. 즉, 해당 레이어에서 local gradient가 0이 되는 순간 이후의 모든 레이어의 그래디언트는 0이 된다. (upstream gradient가 0일 테니 local gradient가 뭐든지간에 downstream gradient 는 무조건 0 이다)
따라서 입력 값이 조금 크거나 작아서 한 번 saturate하게 되면 그 이후부터는 activation layer 이후의 모든 레이어의 가중치가 0이 되고 업데이트 되지 않는다.
두 번째 문제는 Zero-centered 가 아니라는 점.
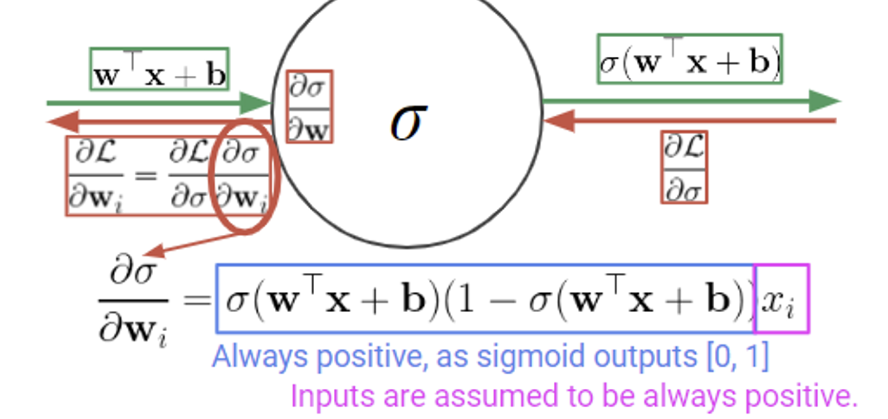
위 사진은 linear함수를 이용하여 sigmoid layer를 지나는 과정을 그렸다. 이때 입력으로 들어오는 x가 모두 양수 라고 가정하자. (사실 이미지만 해도 모든 픽셀 값이 0~255의 값이기에 입력값이 모두 양수인 경우는 생각보다 흔하다)
이때 back propagation을 계산할 때 부호를 잘 보자. 우선 파란색 박스는 sigmoid의 결과값이 항상 [0, 1]의 값이기 때문에 양수가 된다. 분홍색 박스는 아까 입력 x가 양수라 가정했으므로 양수가 된다.
즉, x가 양수면 gradient는 무조건 양수, x가 음수면 gradient도 무조건 음수 가 된다는 말이다.
📌 이게 왜 문제일까?
생각해보면 그래디언트를 계산하는 이유는 입력값 x에 대해 어느 방향으로 가야 하는지 알려주기 위함이다. 그런데 입력값의 부호에 따라서 그래디언트의 부호, 즉 가야하는 방향이 항상 정해져있다면? 그럼 optimal gradient 방향으로 가기 위해서 불필요하게 돌아가야 할 수 있다.
하지만 이 문제는 첫 번째 문제였던 그래디언트 소실 문제보다는 덜 심각하다고 하는데, 그 이유는 mini batch를 사용하기 때문이다. mini batch 내에 여러 샘플을 거치며 gradient를 마지막에 한 번 계산하기 때문에 큰 문제가 아닐 수 있다!
2. Tanh function
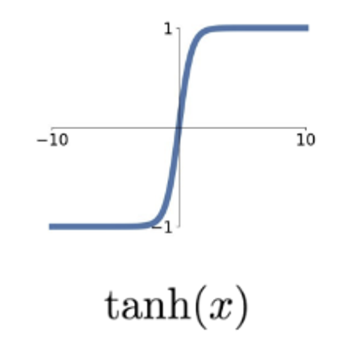
이전 sigmoid 함수에서 Zero-centered 문제는 해결했지만 여전히 그래디언트 소실 문제가 있기 때문에 sigmoid의 근본적인 문제를 해결하지 못했다.
3. ReLU(Rectified Linear Unit)
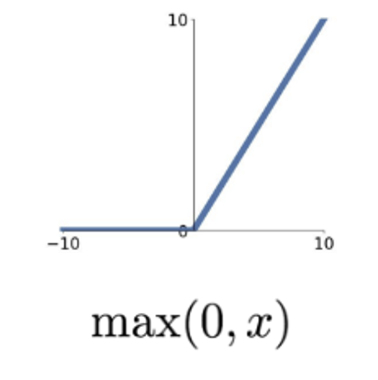
Activation 함수로 자주 사용되는 익숙한 함수 ReLU! 입력값이 양수 면 값 그대로, 음수 면 0을 반환하는 함수다. 계산이 매우 간단하기 때문에 (미분을 계산할 필요가 없다) 수렴 속도가 이전 함수들에 비해 매우 빠르다.
하지만 이 함수에도 문제점은 존재한다. 우선 Zero-centered 가 아니며, x=0에서 미분이 불가능하다. 이 미분 불가능 점에 대한 문제는 실험적으로 큰 문제가 아니라는 사실이 밝혀지긴 했다.
그러나 ReLU의 가장 큰 문제는 Dead RELU . 한 번 음수인 값은 영원히 그래디언트가 0이 되어 다시는 업데이트 되지 못한다는 문제가 있다. 따라서 무작위 값으로 weight를 초기화할 때 음수의 값은 평생 업데이트 될 수 없다는 점. 따라서 이러한 문제를 해결하기 위해 음수 부분의 그래프를 수정하는 함수들이 잇따라 나왔다.
4. Leaky ReLU and ELU
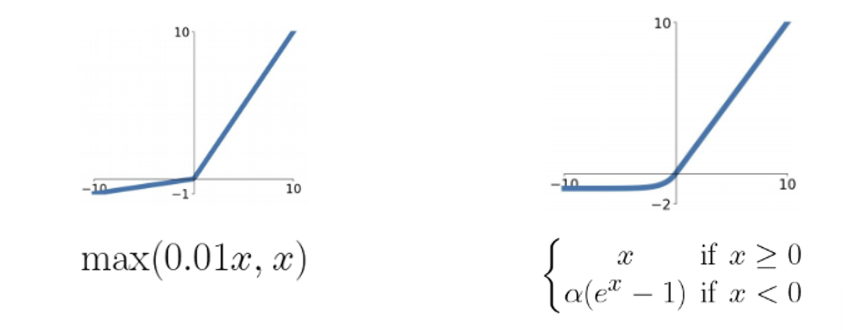
Leaky ReLU 의 경우 음수 부분에 약간의 기울기를 줌으로써 그래디언트를 살리는 것이다. 이때 기울기 값은 하이퍼파라미터 이다. 오른쪽의 ELU 는 추가로 x=0인 지점에서 미분 가능하게끔 만들어 준 함수이다. 물론 계산이 더 복잡하긴 하다.
물론 activation function을 무엇으로 쓰느냐는 모델링하는 사람의 초이스이다. 각각마다 장단점이 분명하므로, activation function으로 무엇을 써야 가장 성능이 좋을지는 up to task!
Data Augmentation
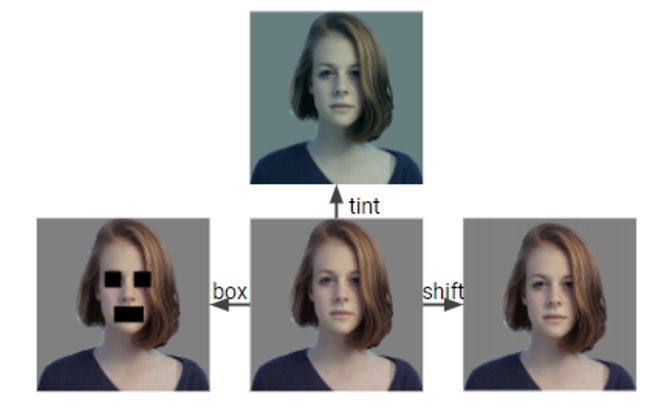
이전 포스팅에서 봤던 사진인데 오늘은 조금 다르게 접근하려고 한다. 원본 사진과 세 가지 variation을 준 사진들인데, 보다시피 인간에게는 semantic 상으로 큰 차이가 없는 사진들이다. shift 는 아예 차이가 없어 보이고, tint 는 색상의 변화가 있긴 하지만 중요한 정보에 대해선 큰 차이가 없다. box 의 경우 그나마 차이가 있다만 여전히 부분적인 정보들(여자, 단발머리 등)을 얻을 수 있다.
하지만 컴퓨터의 입장에서 이 네 장의 사진은 완전히 다른 사진이 될 것이다. 따라서 우리는 한 장의 사진으로도 pixel level 에 변화를 주어 마치 네 장의 서로 다른 사진이 있는 것처럼 모델에 줄 수 있다.
따라서 data augmentation은 semantic 에 변화가 없지만 pixel level에 변화를 주어 여러가지 사진으로 만들어 데이터 수를 늘리는 작업이라 볼 수 있다. Data Augmentation에는 아래와 같은 방식들이 있다.
- Horizontal Flips
- Random Crops
- Scaling
- Color Jitter
Weight Initialization
이번에는 가중치를 어떻게 초기화해야 하는지 보자. 이전에는 그냥 간단하게 랜덤한 수로 초기화한다고 하였지만 이전에 ReLU에서 음수값으로 초기화되면 평생 파라미터 업데이트를 못하는 것과 같이, 어떻게 해야 잘 초기화할 수 있을지 알아보자.
우선 첫 번째 아이디어는 작은 가우시안 랜덤 값으로 초기화하는 것이다.
가우시안 분포에서 랜덤하게 샘플링한 값들에 0.01을 곱해서 초기화를 해보자. 하지만 여기서 문제가 생기는데, 바로 값들이 점점 0으로 몰리는 것이다.
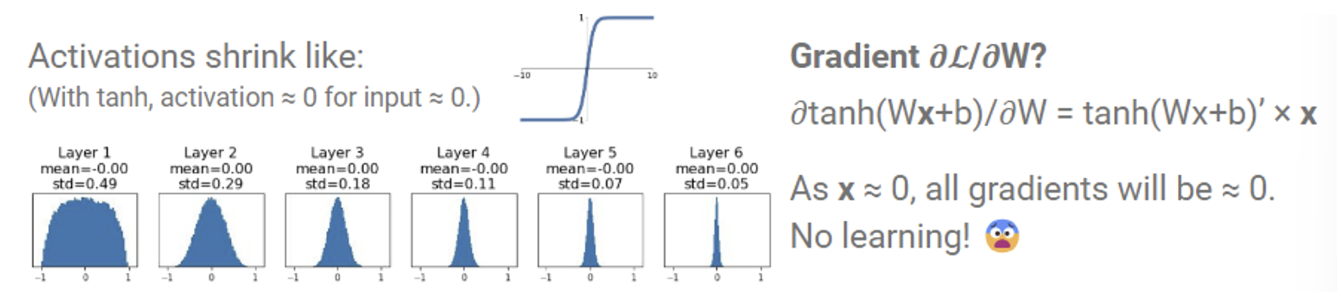
그림을 보면 layer가 얕을 때는 원하는 분포가 나왔지만, 층이 깊어질 수록 점점 값들이 0으로 몰리는 것을 볼 수 있다. 이유는 바로 tanh 함수의 미분 꼴 때문이다. 오른쪽에 tanh 미분 형태를 보면 뒤에 x 가 곱해져 있다. 즉, x가 작은 양수이기 때문에 tanh의 값은 점점 더 작아져 0에 수렴하게 되는 것이다.
그럼 작은 값 대신 큰 가우시안 랜덤 값으로 초기화하는 건 어떨까?
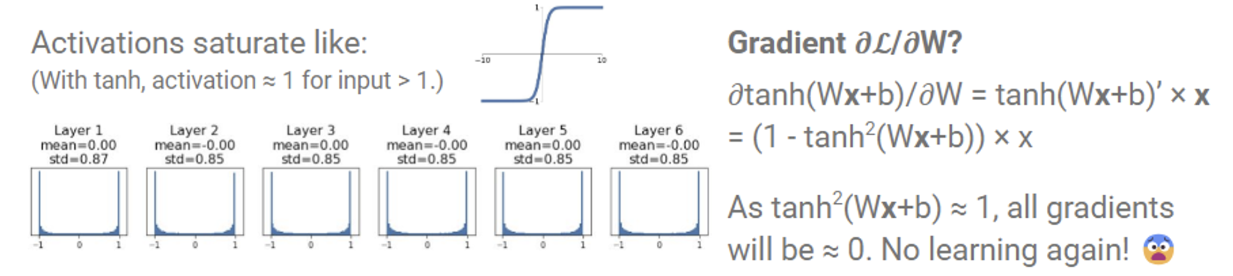
0.01 대신 0.5를 곱해 큰 값으로 초기화를 했더니 이번에는 그래디언트 값들이 모두 -1 또는 1에 집중되는 문제가 생겼다. 또 그래디언트 값도 0으로 수렴하여 파라미터들이 제대로 학습할 수 없다.
이를 어느정도 해결해줄 수 있는 Xaiver Initialization 이 나왔다.
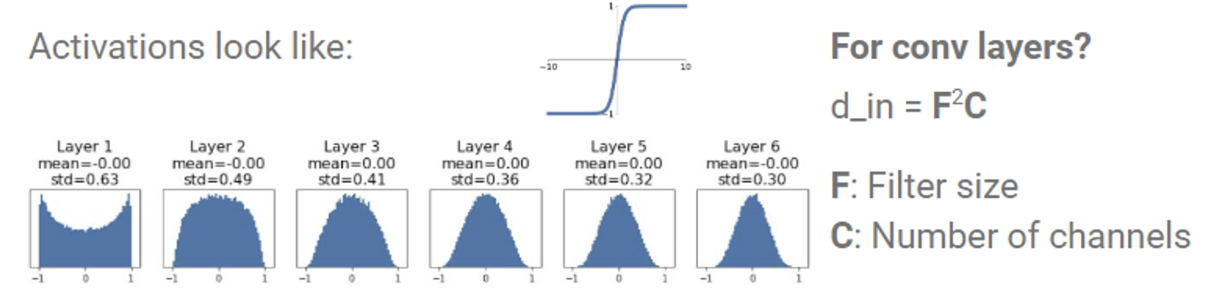
<W = np.random.randn(d_in, d_out) / np.sqrt(d_in)
간단히 설명하면 d_in과 d_out을 최대한 유지하려는 방법이다. avtivation만 지나면 분포가 확 줄어드는 문제를 해결하기 위해서 d_in의 루트값으로 나눠주는 방식으로 가중치 초기화 문제를 완화하려는 시도이다.
오늘은 activation function, data augmentation, 그리고 weight initialization에 대해 설명했다. 다음 포스팅에서 이어서 optimizer 등에 대해 이어가보도록 하겠다. 🤩
