[CV] Neural Network 학습시키기(2)

hmin·2024년 7월 14일

CV Computer Vision Normalization Optimizer Regularization

Computer Vision

목록 보기

5/8

이준석 교수님의 유튜브 강의 Lec 7. Training Neural Networks II 영상을 참고해서 정리한 내용입니다. 다른 출처표기가 없는 이미지는 유튜브 영상에서 가져온 것임을 밝힙니다.

이번 포스팅에서는 특히나 새롭게 얻은 인사이트를 잘 정리해보려고 한다. 이전 포스팅에 이어서 Neural Network를 학습시키는 방법 두 번째 이야기를 이어가보겠다.

Regularization

다시 Recap을 해보자. 머신 러닝 이 뭐라고 했더라..

바로 “Data Driven Approach”

즉 인간의 개입을 최소화 하여 데이터로 부터 학습하고자 하는 것이 머신 러닝이다. 그럼 가장 중요한 것은 “어떤” 데이터가 학습으로 주어지느냐가 될 것이다.

모델은 주어진 학습 데이터에 대해서 훈련을 거친 후에 새로운 데이터를 만났을 때(inference) 이전에 학습한 지식을 활용해서 문제를 풀 것이다. 그런데 이때 우려되는 문제점들이 있다.

만약 모델이 학습 데이터를 무작정 다 암기해버렸다면?

우리가 벼락치기로 기말고사를 공부한다고 생각해보자. 원리를 공부하기보다는 당장 내일 시험에 나올 듯한 문제들을 가지고 머릿 속에 꾸깃 꾸깃 집어넣기 바쁠 것이다. 그럼 시험에서 공부했던 문제들에 대해서는 어느 정도 좋은 점수를 예상할 수 있을 것이다. 하지만 이번에 교수님이 응용 문제를 내셨다면?

안타깝게도 공부한 것을 제대로 쓰지도 못하고 학점에서 처참히 fail할 것이다. 왜냐, 주어진 자료를 단순 암기만 했기 때문에 조금이라도 다른 결의 문제가 나오면 전혀 풀지 못하는 것이다.

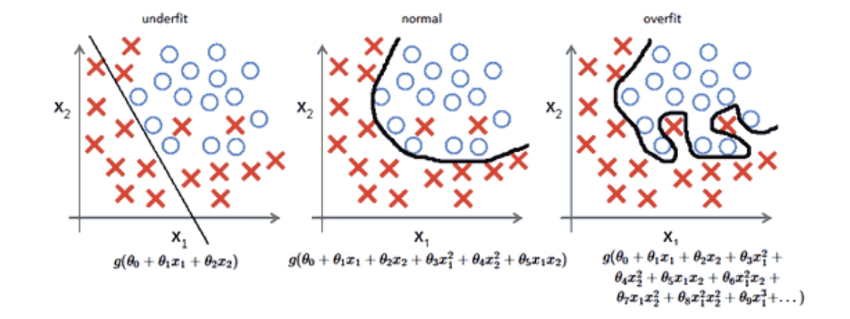
모델도 똑같다. 학습 데이터에서 “공부”를 하는 것은 좋지만 무작정 암기 해버린다면 결국 새로운 데이터에 대해 좋은 점수를 받지 못할 것이다. 우린 이것을 Overfitting 이라고 부른다.

반대로 너무 대충 공부했을 수도 있다. 그럼 학습 데이터에 대해서도 썩 좋은 성능을 내지 못하며 테스트 단계에서도 당연히 잘 못할 것이다. 이걸 Underfitting 이라고 부른다.

우리가 원하는 것은 모델이 학습 데이터에 대해 general한 것을 학습하고 새로운 데이터에 적용했을 때 좋은 성능을 내기 바란다. 즉, overfitting과 underfitting 사이 그 어딘가만큼 학습했으면 한다.

이걸 가능하게 해주는 것이 바로 Regularization 이다.

Regularization은 additional penalty term 으로, 목적 함수에서 파라미터의 제한을 걸어 너무 커지는 것을 방지하는 term이라 볼 수 있다.

📌 왜 파라미터 값이 작게끔 유지하려는 걸까?

3차 함수를 생각해보자. $f = ax^2 + bx + c$ 라는 함수가 있을 때 우리가 학습해야 하는 파라미터는 각 항의 계수 $\theta = \{ a, b, c\}$ 가 될 것이다.
그런데 이 세타 값들이 모두 0일 때를 생각해보면 f는 그냥 상수함수가 된다. 반대로 세타 값들이 크면 클 수록 f는 더 굴곡이 심한 함수가 된다. 즉, 파라미터 값이 크면 클 수록 더 복잡한 함수가 되고, 값이 작을 수록 더 간단한 함수가 된다는 의미다.

앞서 말했든 모델이 복잡할 수록 학습 데이터에 너무 의존적으로 공부하여 overfitting의 문제가 생길 수 있다고 했다. 따라서 우리가 하고 싶은 것은 이 $\theta$ 값이 너무 커지는 것을 방지하여 모델이 너무 복잡해지는 것을 방지하고자 한다.

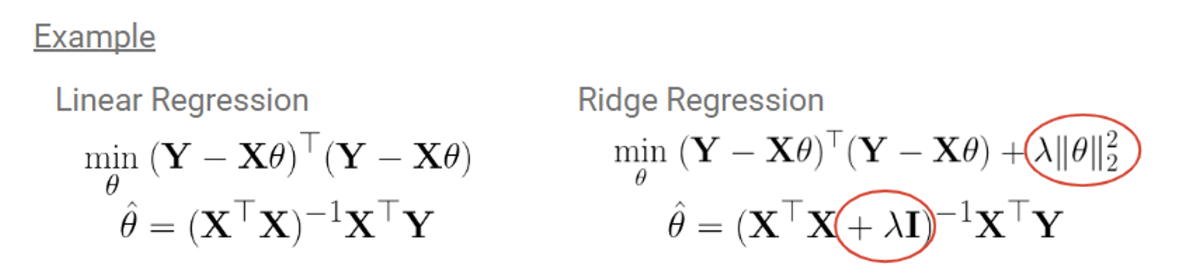
간단한 Linear Regression으로 예를 들어보자. 오른쪽에 지금 추가로 $\lambda ||\theta ||^2_2$ 항을 달아준 것이다. 이게 무슨 의미를 가질까?

결국 우리가 해야하는 것은 전체 loss를 최소화하는 $\theta$ 를 찾는 것이다. 따라서 앞에 $(Y-X \theta )^\top (Y-X\theta)$ 를 줄이면서도 동시에 $||\theta ||^2$ 도 줄여야 하는 것! 이를 통해 세타 값이 너무 커지는 것을 방지할 수 있다.

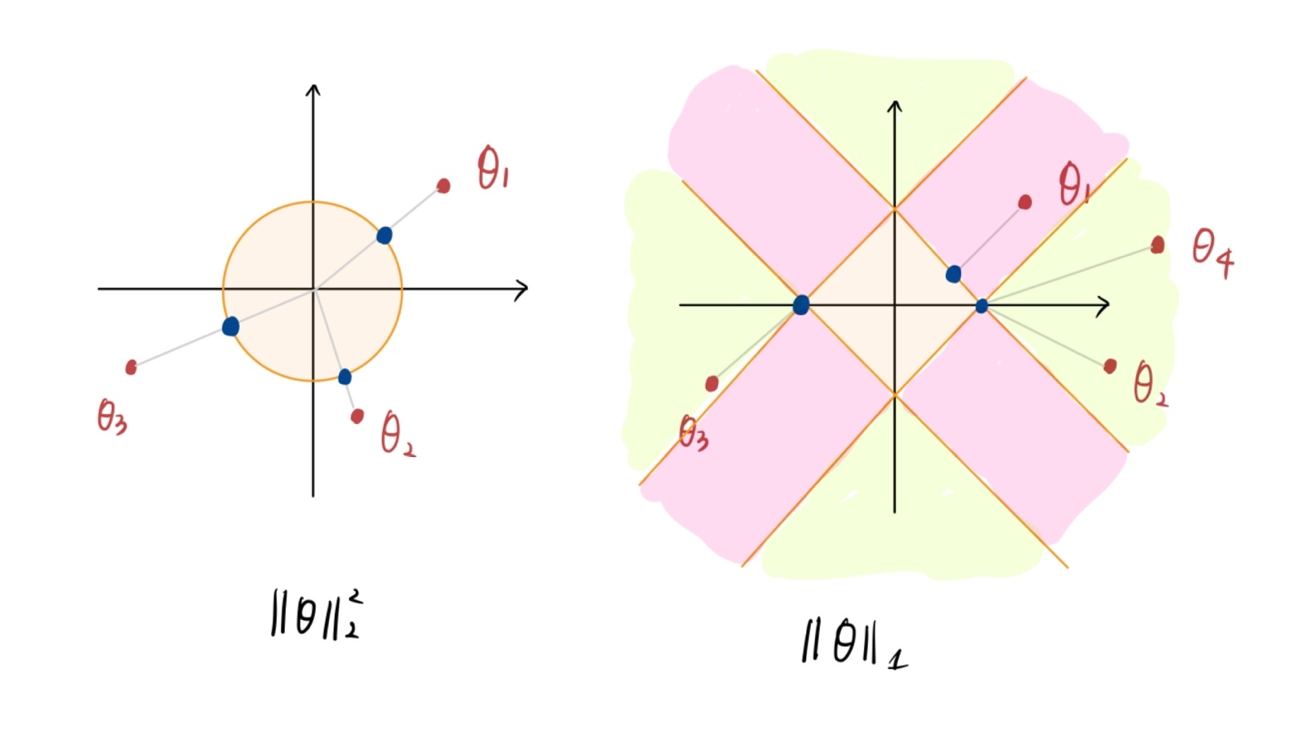
Geometric View

이걸 이번에는 Geometric한 관점에서 보자.

(1) Ridge Regression

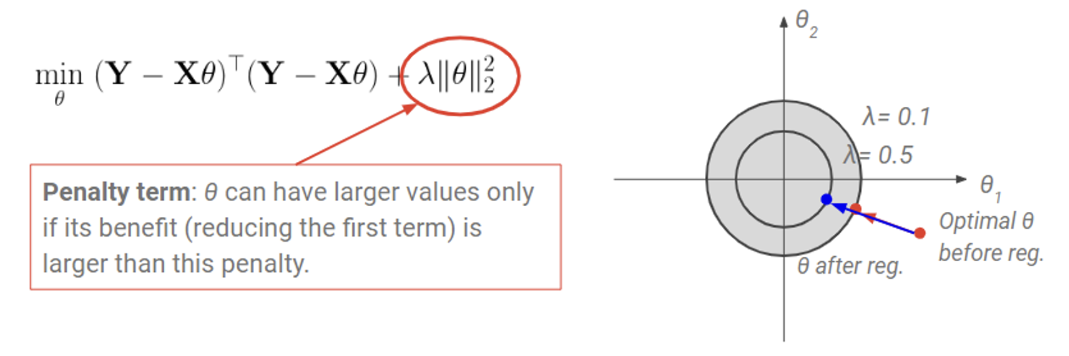
자, 이전에 봤던 linear regression에 regularization을 붙인 형태이다.

우선 오른쪽 아래 빨간 색 점은 regularize term이 없을 때 optimal $\theta$ 를 나타낸 것이다. 이때 regularization은 $\theta ^2$ 꼴이므로 세타가 가질 수 있는 값의 영역은 원 으로 나올 것이다. 이때 regularization을 통해 $\theta$ 는 현재 위치 에서 가장 가까운 원 위의 점으로 간다. $\theta$ 의 값을 작게 유지해주는 것이다.

이번에는 $\lambda$ 를 눈여겨 보자.

$\lambda$ 는 regularization(penalty) term 앞에 붙은 [0, 1] 값을 가지는 상수다. $\lambda=0$ 이면 regularization이 없는 것과 같다. 즉, 원의 영역이 무한히 커지기에 optimal $\theta$는 $(Y-X\theta)^\top (Y-X\theta)$ 로만 결정이 된다.

하지만 $\lambda$ 의 값이 커지면 커질 수록 원의 크기가 작아진다. 즉, $\theta$ 가 가질 수 있는 값이 크게 제한되는 것이다. 따라서 $\lambda$ 값이 1에 가까울 수록 $\theta$ 는 regularization의 영향을 더 크게 받아 더 작은 값을 가지도록 강제되는 것이다.

(2) Lasso Regularization

이번에는 regularization term이 세타에 절댓값을 취해 모두 더한 값이다. 그럼 $\theta$ 가 가질 수 있는 값의 영역은 마름모 꼴이 된다. 근데 여기서 잘 생각해보면 Ridge Regression과 다른 점이 하나 있다.

아까 optimal $\theta$ 가 가장 가까운 원, 또는 마름모 위의 점으로 이동된다고 표현했다.

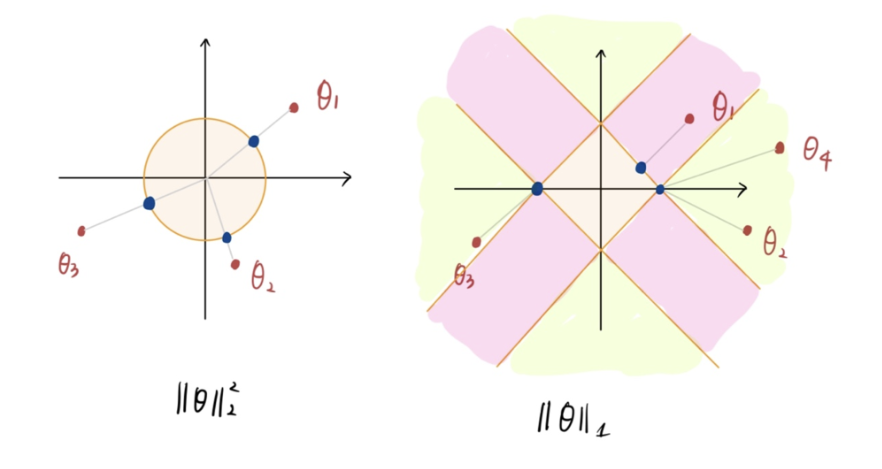
내가 그린 이 꼬질꼬질한 그림을 보자. (이해가 더 잘 될 수 있을진 미지수..ㅎ)

왼쪽 Ridge Regression을 보면 세타가 원 밖에 있으면 쉽게 윈 위의 점으로 매핑시킬 수 있다. 즉, 원 밖의 점은 원 위 모든 점으로 매핑가능하다는 말이다.

하지만 마름모의 경우는 다르다. 세타의 위치에 따라 가장 가까운 마름모 위의 점 이 상당히 제한적이다. 핑크색으로 칠해놓은 영역 위의 점은 무조건 마름모의 모서리 로 매핑이 될 것이다. 그리고 초록색 영역 위 점만 마름모의 변에 매핑이 될 것이다. 당연히 이 영역을 무한대로 그리면 핑크색 영역보다 초록색 영역이 훨씬 더 클 것이며 마름모의 모서리 로 매핑 될 확률이 크다는 소리다.

하지만 모서리의 점은 $\theta_1=0$ 또는 $\theta_2 = 0$ 인 지점이다. 따라서 Lasso Regularization 을 따르면 세타의 값 중 일부가 0으로 매핑되는 경우가 상당히 많으며, 이에 따라서 $\theta$ 는 Sparse 해진다는 것이다!

💡 정리해보자면 Ridge Regression은 세타의 크기를 균등하게 줄여주는 역할을 하는 반면에, Lasso Regularization은 필요없는 세타는 완전히 0으로 만들어 sparse하게 만드는 역할을 한다.

(여기 부분을 듣다가 진짜 눈 동그래졌다. 이걸 이전에도 공부했지만 이해가 잘 안가서 그냥 스킵했었는데, 오늘에서야 비로소 완전히 이해했다…)

Optimization beyond SGD

이전에는 Optimization이라고 해서 Stochastic Gradient Descend 만 다루었다. 물론 여기서 더 발전된 아이디어들이 있으니, 하나씩 알아보자.

What is Momentum?

모멘텀. 물리학에서 따온 용어이다. 물리학에서 사용되는 “모멘텀”은 질량과 속도를 곱한 것으로 한국어로 “운동량”이라 한다. 하지만 여기서 사용되는 모멘텀은 관성 에 더 가까운 뜻으로 사용된다. 즉, 가던 방향으로 계속 가려는 성질을 나타낸다.

우리는 gradient descend의 방법으로 optimal한 점을 찾는다. 이때 문제는 global minima가 아니라 local minima 나 saddle point 에 한 번 잘못 들어가면 gradient = 0이 되어 빠져나오기 힘들다는 것. 이때 이전에 가던 방향으로 가려는 힘을 더해준다면 잘못된 minima에 더 잘 빠져나올 수 있을 것이다.

따라서 기존에 파라미터를 업데이트 하는 방식에서 momentum term을 추가한다. $v_t$ 는 이전 업데이트에 대한 정보를 담고 있어, 현재 파라미터를 업데이트 할 때 이전 업데이트 정보를 활용하겠다는 의미로 볼 수 있다.

AdaGrad

AdaGrad는 Adaptive Gradient의 줄임말로 그래디언트 계산들 dimension에 따라 차이를 두자는 뜻이다. 이전까지는 모든 그래디언트에 learning rate을 곱해 동일하게 업데이트를 했다. 하지만 이번에는 dimension마다 업데이트 정도에 차이를 두겠다는 뜻.

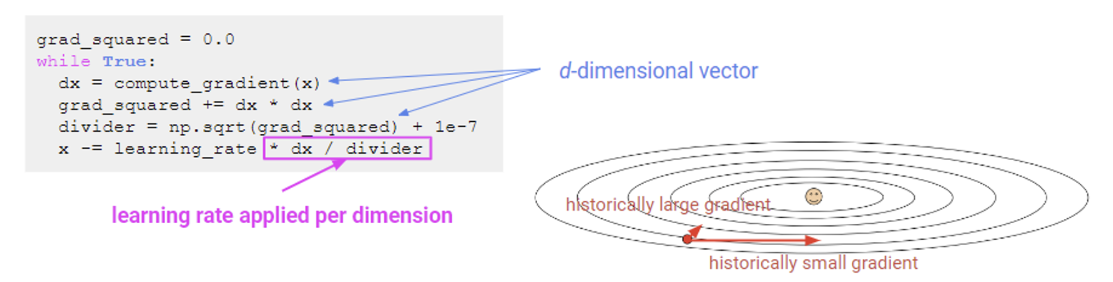
dx = compute_gradient(x)  // dx: 현재 위치에서의 gradient
grad_squared += dx * dx  // grad_squred: 그래디언트의 제곱 합, 이전 그래디언트 값을 저장하고 있음
divider = np.sqrt(grad_squared) + le-7  // 0으로 나누는 것을 방지하기 위해 작은 상수 더해줌

x -= learning_rate * dx / divider  // 이전까지의 그래디언트 제곱 합으로 나눠줌

💡 이게 무슨 의미를 가지는지 보자.

grad_squared는 이전까지의 그래디언트 값의 제곱 합을 저장한다. 이때 dx는 d-dimensional vector이기 때문에 각 dimension 별로 그래디언트 제곱 합을 저장하는 셈이다.

그리고 파라미터를 업데이트 할 때 이 값으로 나눠준다. 만약 이전에 큰 그래디언트를 갖는 dimension이라면, 즉 변화량이 큰(속도가 큰) dimension의 경우엔 grad_squared 값이 클 것이므로 나눠주는 값이 크다. 이는 “이전에 빠르게 내려왔으니 이번에는 천천히 내려가~”라는 의미.

반대로 이전에 작은 그래디언트를 갖는 dimension의 경우 작은 값으로 나눠주니 “천천히 내려왔으니 좀 더 속도를 내서 내려가~”라는 의미로 해석될 수 있다.

RMSProp

앞서 봤던 AdaGrad의 문제가 있다. 바로 학습을 하면 할 수록 결국 grad_squared의 값은 계속 커지므로 나중에는 모든 dimension에 대해 값이 커지게 되므로 수렴 속도가 매우 느려질 것이다.

따라서 RMSProp에서는 “옛날 업데이트 정보보다 최신 업데이트 정보에 좀 더 힘을 실어주자”라는 아이디어로 나온 방법이다.

dx = compute_gradient(x)
grad_squared += dr * grad_squared + (1 - dr) * dx * dx  // only Difference!
divider = np.sqrt(grad_squared) + le-7  

x -= learning_rate * dx / divider

dr(=decay rate) 파라미터를 둬서 예전 그래디언트 정보와 현재 그래디언트 정보 사이에 weight을 다르게 준다는 의미다. 딱 이거 하나 달라졌다.

Adam

AdaGrad + RMSProp을 합친 형태.

first_moment = 0.0
second_moment = 0.0
while True:
  dx = compute_gradient(x)
  first_moment = beta1 * first_moment + (1 - beta1) * dx
  second_moment = beta2 * second_moment + (1 - beta2) * dx * dx
  divider = np.sqrt(second_moment) + 1e-7
  x -= learning_rate * first_moment / divider

요즘 가장 많이 쓰이는 optimizer이기도 하다.

Batch Normalization

이전에 데이터 전처리에 대해서 이야기 할 때 Normalization에 대해 언급했었다.

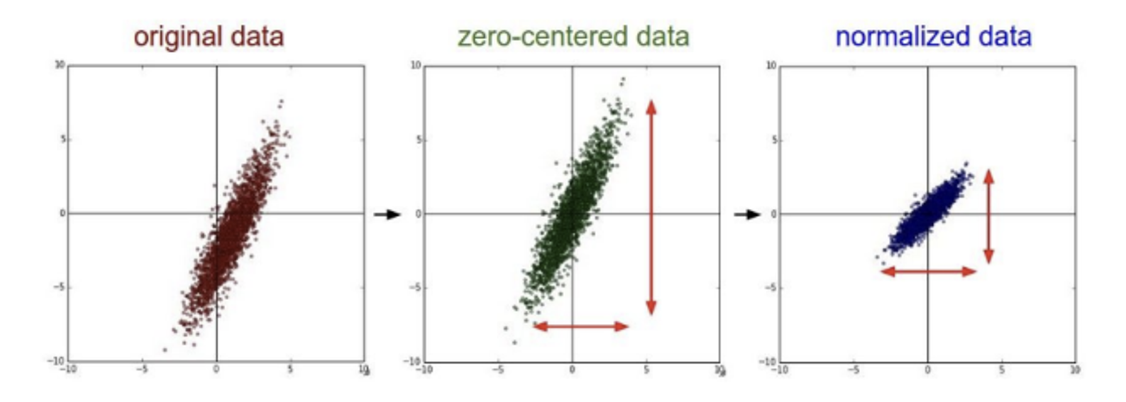
데이터를 normalized 시킨다면 activation을 지나면서 생기는 문제들을 어느정도 해결할 수 있을 것이라는 생각에서 나온 아이디어. (예를 들어 데이터가 다 음수면 ReLU 들어가는 순간 Dead ReLU에 빠져버리는 등의 문제가 생기므로 어느정도 전처리하고 들어가면 좋다)

하지만 문제는 전처리하는 것은 좋지만 이 효과는 첫 번째 레이어 에만 적용이 된다는 것이다. 중간 레이어에도 이러한 처리를 통해 효율적으로 학습할 수 있게 만들 순 없을까?

이 아이디어가 바로 Batch Normalization 이다.

우린 학습시킬 때 mini batch 를 사용하는데, 이 배치 안에 들어있는 샘플들에 대해서 평균 과 분산 을 계산해 Normalization을 시키겠다는 의도이다.

N개의 샘플이 들어왔을 때 전체에 대한 평균과 분산을 구하고 x를 normalize 시켜주면 된다. 어려운 것은 없다.

하지만 문제는… 이렇게 내 마음대로 입력값 바꿔줘도 되는건가? 🤔💭

답은 당연히 안된다는 것. 입력 값을 내 마음대로 바꿔버리면 레이어가 학습하는 것에 변화가 생겨버린다. 따라서 normalized 한 후에 다시 복구 해주는 과정이 필요하다.

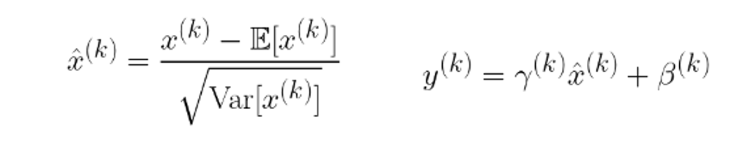
여기서는 새로운 파라미터 $\gamma , \beta$ 를 둬서 학습으로 이 값을 얻게끔 한다. 이렇게 예쁘게 normalized 를 시켜도 ReLU만 지나면 음수인 부분은 모두 0으로 매핑되어 버린다. 따라서 $\gamma$ 와 $\beta$ 로 Scaling과 Translate를 시켜주려는 목적이다. 이때 어떻게 transform 시킬지는 모델이 알아서 적절히 학습할 것이다.

Test 단계에서 Batch Normalization은 Deterministic 한 값을 사용한다. 학습 단계에서는 데이터를 배치 단위로 받기 때문에 평균과 분산을 계산할 수 있었지만 테스트 단계에서는 이러한 계산이 어렵다. 따라서 학습 단계에서 미리 계산한 평균과 분산을 그대로 가져가 test 단계에서 사용한다.

ref: https://gaussian37.github.io/dl-concept-batchnorm/

물론 Batch Normalization에도 한계점이 있다.

mini batch 마다의 평균과 분산을 계산하는 것이기 때문에 이때 데이터가 i.i.d. 하게 샘플링된다는 가정이 있어야 한다. 이게 없으면 mini batch마다의 분포가 다를 수 있기에 배치마다 이러한 연산을 하는 게 위험할 수 있다. 또, train에서 미리 계산한 평균 과 분산 을 test에서 그대로 적용하기 때문에 분포가 달라지면 test 단계에서 문제가 생길 수 밖에 없다.

이번 포스팅에서는 Regularization, Optimizer, Normalization에 대해알아보았다. 언제든 필요할 때마다 꺼내보기 쉽게 정리하려고 했는데.. 깔끔한지는 모르겠지만 좋은 인사이트를 얻을 수 있는 강의였다. 😀