이번 글은 대학교 강의에서 공부한 내용을 바탕으로 정리한 글입니다. 출처가 없는 사진 자료는 강의 자료 ppt에서 가져왔음을 밝힙니다.

이전 포스팅에서 VAE에 대해 설명을 했다. 이번에는 이어서 Normalizing flow에 대해 알아보자. 여긴 내용이 길어서 두 편으로 나눠서 포스팅할 예정이다. 이번 포스팅에서는 수학적 백그라운드에 대해 다루고, 다음 포스팅에서 Normalizing flow 모델들에 대해 알아보도록 하자.

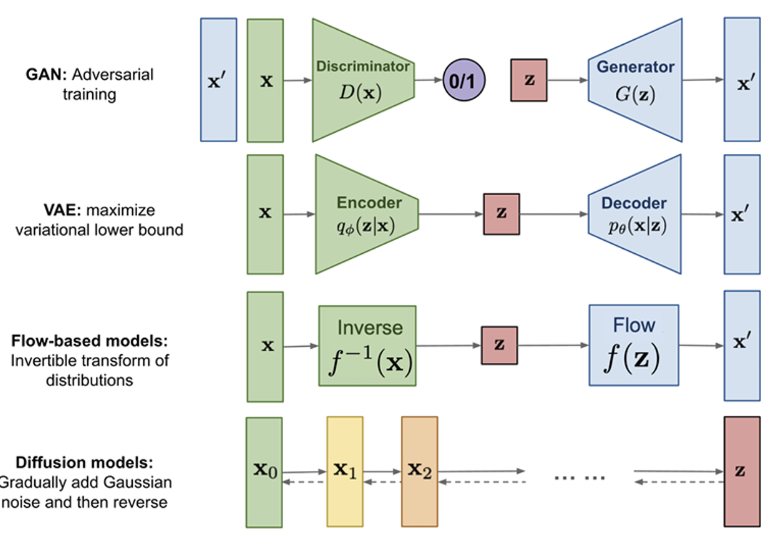
이번에는 Flow-based model을 보자. 모델을 보면 사실 바로 위에 있는 VAE와 비슷해보이면서도 다르다. latent space 가 중간에 있고 앞뒤로 Inverse 와 Flow 가 있다. 여긴 VAE와 다르게 인코더/디코더 베이스가 아니라 invertible function 으로 되어있다. 그럼 Normalizing flow가 뭔지 한 번 알아보자.

📌 Normalizing Flows

우선 Normalizing Flows 의 용어부터 알아보자.

• Normalizing: Change of variables 메서드를 이용해 쉽고 tractable한 density로 부터 복잡한 density를 끌어내는 것
  
• Flow: Invertible transformation이 연달아 시퀀스로 이어져있는 것
  

참고로 Normalizing은 우리가 흔히 알고있는 확률에서 사용하는 ‘정규화’(평균을 빼고 분산으로 나누는)와 다르다. 여기선 distribution을 내가 잘 아는 것에서 부터 원하는 것으로 transformation을 한다는 의미에서 normalizing 이란 용어를 쓰지 않았을까 추측된다.

우선 Normalizing Flow를 알기 위해 알고 있어야 하는 두 가지 개념을 먼저 정리하고 가자.

1. Change of Variable

Change of variable은 쉬운 distribution을 invertible transformation 을 통해 우리가 원하는 복잡한 distribution을 얻는 과정이다. 우선 single variable인 경우를 통해 어떤 식으로 이루어지는지 보자.

r.v. z 가 주어지고 이 변수의 density가 $\pi(z)$로 잘 알려져 있다고 하자. 여기서 잘 알려진 probability density란 uniform, gaussian 등이 있을 것이다.

우리가 원하는 것은 z의 1대 1 매핑 함수 $x = f(z)$를 이용하여 새로운 r.v. x의 분포를 알고자 한다.

첫 번째 줄은 $p(x)$와 $\pi(z)$ 모두 확률 분포이므로 합이 1이라는 점을 이용한 식이다. 아래는 이를 그대로 치환 및 전개했을 때의 결과이다. 즉, 이를 이용하면 p(x)의 분포를 알 수 있다. 물론 전제조건은 f 가 invertible 하다는 것이다.

이를 multivariate로 확장하면 다 동일하고 마지막에 $d f^{-1} \over dx$에만 차이가 있다. x가 더이상 단일 변수가 아니므로 각각의 x에 대해 f를 미분한 jacobian matrix 가 필요하다.

📢 쉽게 생각해보자. 변수 z가 있고, x = f(z) = z^2라고 하면 f를 한 번 지날 때마다 최고 차수는 2배씩 커진다. 한 번 지나면 일차식이 이차식으로 바뀌고, 또 한 번 지나면 사차식이 된다. 따라서 f를 지나면 지날 수록 **훨씬 더 복잡한 함수**를 만들 수 있다. 이러한 아이디어를 그대로 확률분포에 적용한 것이라 해석할 수 있다.

2. Jacobian Determinant

사실 Jacobian와 Determinant는 예…전에 공부 많이 했었는데 다 잊어버렸다. 안하고 그냥 감으로 느끼고 가려고 했는데, 뒤로 갈 수록 이해가 안가서 결국 다시 공부했다. 위키피디아에서 둘 사이의 관계를 잘 설명했길래 이를 많이 참고했다.

간단히 설명하면 이렇다.

Jacobian은 입력 공간에 f라는 변환을 가했을 때, 출력 공간에 얼마만큼의 크기/부피 변화가 있는지 보여주는 행렬이다.

Jacobian의 원소들은 입력 x (x1,…,xn)에 대한 f (f1,…,fm)의 일차 도함수 값이 들어있다. 따라서 Jacobian은 입력에 대한 출력 공간의 변화량 이라 해석할 수 있다.

determinant는 scalar로 표현되어, 그러한 변화량을 하나의 값으로 보여주는 역할을 한다. 만약 det(J) > 1이라면 공간의 크기/부피가 확장되었음을, <1이면 축소되었음을 보여준다.

위에서 봤던 change of variable의 핵심은 integral 을 계산할 때 변수를 치환하는 것이다. 이때 그냥 치환해선 안되고, 치환 전의 좌표공간과 치환 후의 좌표공간을 매치시켜줘야 한다. 이때 둘 사이 변화량을 곱해줘야지만 두 좌표공간의 변화량을 알 수 있고, 여기서 det(J)가 사용되는 것이다.

즉, x 공간에서 z 공간으로 변환하기 위해선 그 좌표계의 변화량을 따져야 하므로

dx에서 dz로 변환하고자 한다면 det(J)를 곱해줘야 한다. 다시 말해 normalization 을 해야한다는 말이다. Normalizing flow에 사용되는 개념은 여기까지 이므로 이정도만 정리하고 바로 normalizing flow로 들어가보자.

Normalizing Flows

그럼 처음에 했던 normalizing flow의 용어 정의를 다시 보자.

Normalizing은 Change of variables 를 이용해 쉬운 분포에서 우리가 원하는 복잡한 분포로 넘어가는 매서드라고 했다. 그럼 아까 봤던 change of variables의 정의를 대입해보면 “쉬운”, “잘 알려진”, “tractable”한 분포는 z의 분포였던 $\pi(\mathbf{z})$이다.

그럼 우리가 알고자 하는 “복잡한”, “intractable”한 분포가 바로 $p(\mathbf{x})$가 되는 것이다. 그리고 p(x)를 알기 위해선 $f^{-1}$이 필요한 것이다. 따라서 flow 는 이러한 inverted functions이 시퀀스로 이어진 것을 의미한다.

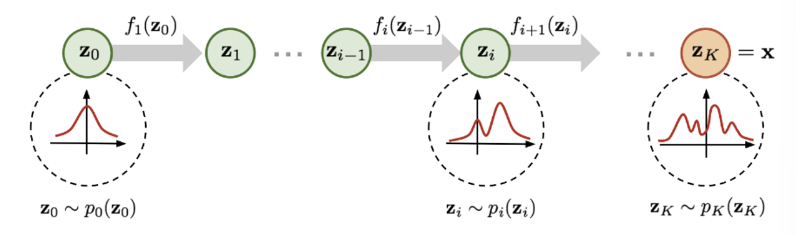
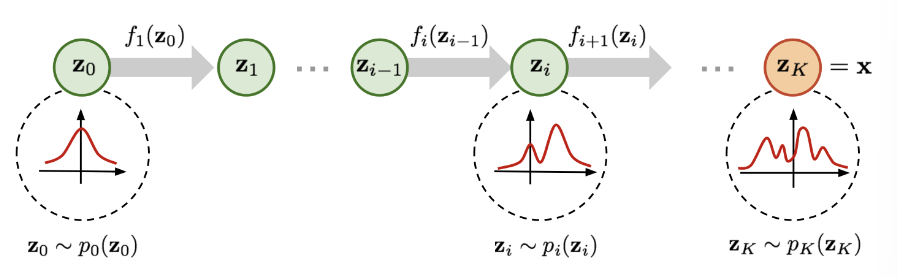
위 figure를 보면 이제 Normalizing Flow가 어떻게 동작하는 모델인지 알 수 있을 것이다.

가장 왼쪽에 정규분포가 그려져 있다. 쉽고 잘 알려진 확률 분포를 나타낸다. 이를 이용해 transformation function을 한 번 지날 때마다 새로운 변수로 변환된다. 이 작업을 여러번 시퀀셜하게 하면 결과적으로 우리가 원하는 복잡한 함수를 만들 수 있다.

이때 x를 $z_K$라 하면 결국 $z_0$부터 $z_K$까지 시퀀셜하게 이전 값을 invertible 함수의 입력으로 주는 것이다.

그럼 이제 p(x)를 알기 위해 중간 단계인 $p_i(z_i)$에 대한 식을 도출해보면 아래와 같다.

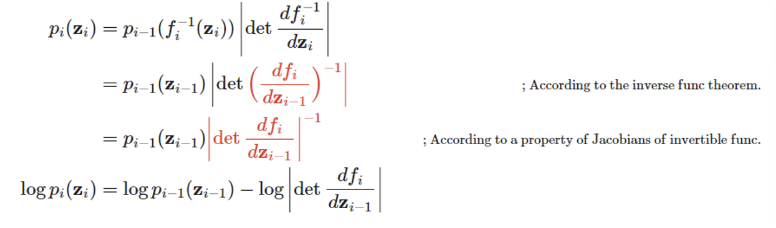
참고로 빨간색으로 표기된 부분은 inverse func theorem과 Jacobian theorem과 연관된 부분이니 더 자세한 내용은 여기를 참고하면 될 것 같다.

이렇게 $\log p_i (z_i)$를 구했다면 이제 전체 단계, 즉 $z_0$부터 $z_K$까지의 흐름을 수식으로 나타내보자.

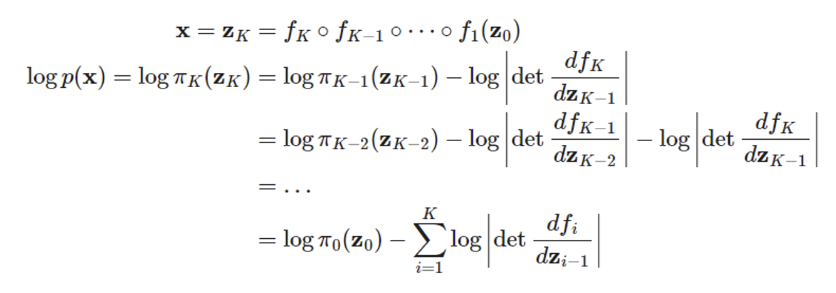
결국 x를 구하기 위해서는 $z_0$부터 K번 f를 합성하면 된다. 후에 ML로 학습시키기 위해 log likelihood 를 구해보면 위와 같이 나온다. 따라서 p(x)를 구하기 위해서는 f에 대한 Jacobian matrix의 det를 연속적으로 구해야 함을 알 수 있다.

따라서 여기서 알 수 있는 transformation function f 의 특징은

• 쉽게 invert할 수 있어야 하고
• Jacobian det 계산이 쉬워야 한다.

위 조건을 만족하는 f가 존재한다면 우린 쉽게 p(x)를 구할 수 있을 것이다.

여기서 알 수 있는 Normalizing Flow과 VAE의 차이점이 바로 p(x)를 얻을 수 있는가 이다.

💡 다시 VAE로 돌아가보자.

보다시피 VAE는 p(x)를 explicit 하게 추정할 수 없다. 그러니 따라서 log likelihood를 바로 추정하여 이를 maximize 시키는 것 자체가 불가능한 것이다. 따라서 우리는 VAE를 학습시킬 때 그 lower bound 를 maximize하는 방향으로 학습시켰다.

그래서 ELBO 라는 개념이 나왔던 것이고, 우린 p(x)를 알 수 있는 방법이 없으므로 대신해서 그 하한 값인 ELBO를 최대화하는 방향으로 학습을 진행했다.

하지만 Normalizing flow는 그럴 필요가 없다. p(x)를 explicit 하게 알고 있으니까! 방금 구했던 $\log p(x)$를 그래도 maximize하는 방향으로 학습하면 된다.

이때까지의 내용을 한 장으로 정리하면 이렇다.

글씨가 날라다니긴 하다만.. 결론은 invertible function f 를 가지고 쉬운 tractable한 분포로부터 우리가 원하는 분포를 만들어 낼 수 있으며, 이때 p(x)를 explicit 하게 구할 수 있기에 바로 maximize하는 방향으로 학습하면 된다는 것.

다음 포스팅에서 NICE, RealNVP, GLOW, MintNet 모델들에 대해 알아보며 normalizing flow를 실제로 어떻게 구현했는지 알아보겠다.