이번 글은 대학교 강의에서 공부한 내용을 바탕으로 정리한 글입니다. 출처가 없는 사진 자료는 강의 자료 ppt에서 가져왔음을 밝힙니다.

이전 포스팅에서 Normalizing flow의 기초 지식들에 대해 공부했다.
그럼 이러한 Normalizing flow를 이용한 모델들에 대해 알아보자. 가장 먼저 알아볼 모델은 NICE 로 2015년에 등재된 논문이다.

NICE

N onlinear I ndependent C omponents E stimation
📄paper: https://arxiv.org/pdf/1410.8516.pdf

NICE 모델의 특징을 정리해보면 다음과 같다.

• density에 대해 Volume Preserving transformation 사용
• 두 가지 invertible transformations 사용 (Additive coupling layers + Rescaling layers)
  

이 모델에서 사용하는 transformation에 대해 더 자세히 알아보자.

우선 가장 큰 문제는 layer를 invertible하게 만드는 것이다. 입력으로 들어온 값들에 대해 invertible한 변환을 취해줘야지 normalizing flow가 성립한다. 그럼 어떻게 f를 만들지?

사실 가장 간단한 transformation은 linear transformation 일 것이다.

생각해보면 linear transformation은 언제든, 어떤 입력이 들어오던지 간에 invertible하다.

짠. linear transformation은 언제나 invertible하다. NICE는 이러한 아이디어에서 착안한 모델로, affine transformation 을 이용한 방법이다.

우선 입력으로 들어온 z를 disjoint subsets $z = \{z_A, z_B\}$으로 나눈다.

우선 z에서 x로 가는 forward mapping을 보면 다음과 같이 정의되어 있다.

Forward Mapping $z \rightarrow x$

• $\mathbf{x}_A = \mathbf{z}_A$ : identity transformation
• $\mathbf{x}_B = \mathbf{z}_B + m_\theta (\mathbf{z}_A)$ : Coupling law

입력으로 들어온 z에 대해 $\mathbf{z}_A$은 identity transformation을 취하고(변화 없이 그대로 출력으로 전달), 나머지에 대해선 특정 neural network m을 지난 후 $\mathbf{z}_B$를 더한다.

여기서 임의의 neural network m에 non-linearity 가 포함되어 있다. 하지만 $\mathbf{x}_B$를 구하는 변환 자체는 affine transformation 으로 linear transformation 이다. (Scaling과 Translation 변환)

Coupling law에 대해선 조금 이따가 설명하기로 하고 우선 이 forward mapping에 대한 Jacobian 행렬을 구해보자.

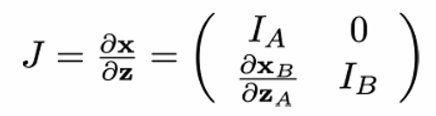
Jacobian matrix가 low triangular 하게 나옴을 알 수 있다. 이때 det 을 구하려면 대각 원소들을 모두 곱하면 된다. (triangular matrix에서의 det는 대각 원소들의 곱으로 쉽게 구할 수 있다.)

Jacobian의 determinant를 구하면 아주 아름답게 1 이 나옴을 알 수 있다.

본래 Jacobian determinant는 “변화량”을 나타내는 값이다. (잘 생각해보면 mapping 함수의 1차 미분식이니, 변화량으로 해석하는 것이 적절한 것 같다.)

따라서 입력 공간에 대한 출력 공간의 변화량을 뜻하는데, 그게 1이라고 하는 것은 결국 변화가 없다는 말이다. 즉, 둘 사이의 volume preserve 가 성립한다는 말이 된다.

사실 이 volume preserving한 성질이 generative model에게는 큰 제약이나 마찬가지다. 아무리 transformation을 해도 volume에는 변화가 없다. 즉, 새로운 데이터를 생성하는 표현력에 있어서 큰 제약이 생기는 것이다.

따라서 NICE에서 이러한 제약을 완화하기 위해서 마지막 layer에서 rescaling transformation을 하는데, $x_i = s_i z_i$로 변환한다. 이때 det of jacobian은 동일한 방식으로 계산하면,

Coupling Method

그럼 이제 coupling method가 뭔지 자세히 알아보자. coupling method는 변수를 둘로 나눈 후 transformation 등 연산을 하고, 후에 다시 합치는 작업을 말한다.

이는 다음과 같은 과정을 거친다.

이를 도식으로 보면 더 쉽다.

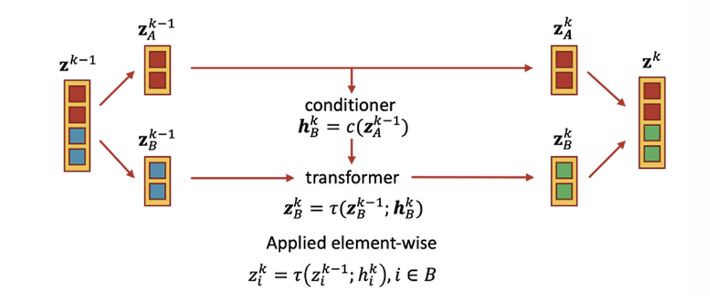
$\mathbf{z}_A$에 대해서는 identity하게 넘겨준다. 그리고 이를 이용해서 조건 $h_B^k$를 만든다. 후에 $\mathbf{z}_B$를 계산할 때 입력과 조건을 통해 invertible한 transformation을 적용한다.

inverse는 위 연산을 그대로 반대로 해주면 된다.

---

Real NVP

Real -valued N on- V olume Preserving
📄paper: https://arxiv.org/pdf/1605.08803.pdf

이번에는 Real NVP를 알아보자. 전반적인 구조는 NICE와 동일하지만 이름에도 나와있듯이 이번에는 volume이 preserve되지 않는 방식이다. 구체적으로는 affine transformation 의 scale, translation(bias) 항이 파라미터로 되어있다.NICE에서는 translation(bias) 항만 있었다면 RealNVP는 scaling까지 시켜줘서 volume preserving한 특성을 없앤 것이다.

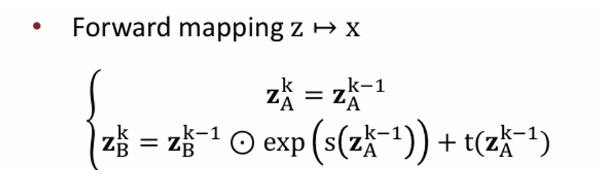
NICE 에서는 $\mathbf{z}_A$에서 neural network를 지나 만든 condition $h_B^K$로 affine transformation을 하는 방식이었다. 하지만 RealNVP는 이때 condition으로 $s$와 $t$를 생성한다. s는 scaling, t는 translation을 하는 파라미터이다.

그럼 여기서도 Jacobian을 구해보자.
(아래 수식은 여기서 가져온 것이다. 더 자세한 수식은 이 블로그를 잘 참고하면 좋을 것 같다.)

det가 무조건 양수로만 나온다는 것을 알 수 있다.

NICE 에서는 det(J) = 1로 고정되어 있기 때문에 volume preserving이 되는 문제점이 있었다. 이게 왜 문제점이냐 하면은 좌표 공간을 새롭게 바꾸는데도 volume이 보존되기 때문에 표현력이 떨어지고 변환에 있어서 제약이 생기게 된다. 따라서 더 복잡한 데이터 분포를 충분히 표현하는 데에 한계가 있기 때문에 NICE 에서는 후반 레이어에 일부로 rescaling layer 을 추가하기도 했다.

RealNVP 에서는 이러한 제약을 없애기 위해서 non-volume preserving한 방법을 택했다. NICE처럼 invertible 계산이 쉬우면서도 jacobian matrix가 triangular 모양을 가지도록 affine transformation을 사용하면서도 더 복잡한 데이터를 표현할 수 있도록 만든 것이다.

ref: https://deepseow.tistory.com/46

Batch Normalization

RealNVP에서는 모든 coupling layer의 output에 대해 batch normalization 을 적용했다. NICE에서 rescaling layer를 따로 둔 것처럼 여기서는 coupling layer의 결과값에 대해서 정규화를 시켜주는 것이다.

이에 따라서 jacobian determinant는 다음과 같이 나온다.

---

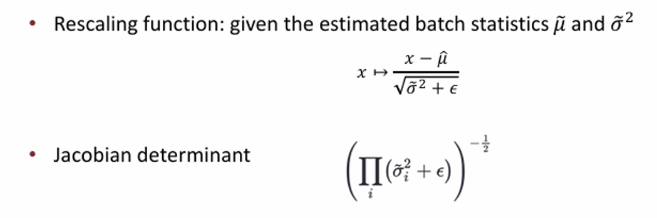
Glow

Generative flow
📄 paper: https://arxiv.org/pdf/1807.03039.pdf

Glow는 이전 모델들을 확장하면서 invertible한 1*1 conv를 이용해 채널 간의 연산을 가능하게 한 모델이다.

한 step의 flow는 아래와 같이 세 개의 substeps를 거친다.

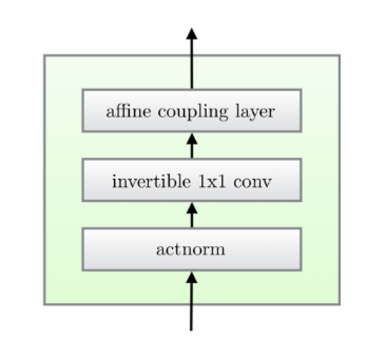
1) Activation normalization (actnorm)

여기서 채널 마다 affine transformation(scaling + bias translation)을 적용하는 층이다. Batch normalization 과 유사하지만 여기선 mini batch size가 1인 경우에도 작동한다.

따라서 배치 정규화는 mini batch 안의 샘플들에 대해서 평균과 분산을 계산해 정규화를 했지만, actnorm에서는 하나의 샘플 내에 채널별로 평균과 분산을 계산해 정규화 한다.

📌 결국 batch size = 1일 때도 작동하는 채널 별 normalization이라 생각하면 될 것 같다.

이때 레이의 초기화는 가장 첫 mini batch 샘플이 들어왔을 때 actnorm의 결과가 평균 = 0, 분산 = 1을 갖도록 하는 값들로 초기화 한다. 즉, data dependent initialization 을 수행한다.

2) Invertible 1x1 conv

1x1 conv는 h, w는 보존하면서 채널에만 영향을 준다. 이때 이 1x1 filter을 잘 설계하면 채널의 순서를 바꾼 것 같이 만들 수 있으며 이를 통해 channel의 순서를 무작위로 섞어서 학습하게 되는 효과를 준다. 이에 따라서 데이터 내의 복잡한 dependency나 correlations를 파악할 수 있다.

이렇게 생각해보자.

• 입력: $\mathbf{h}$ = h x w x c
• 커널(가중치): $\mathbf{W}$ = c x c
• 출력: h x w x c

이때 커널의 크기는 입력 채널에 의해 결정이 된다. 입력 차원을 (hxw) x c라 생각하면 커널과 내적을 해 동일한 크기의 출력을 구할 수 있다.

1x1 conv 작용을 함수로 보면 이에 대해 입력 텐서로 미분하여 자코비안을 구할 수 있다.

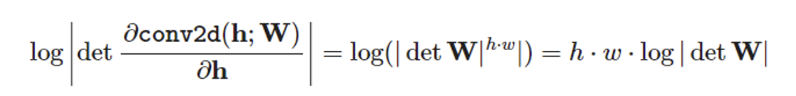
conv의 출력은 결국 h과 W의 곱셈이므로 미분하면 W만 남는다. 이때 각각의 Y(output tensor)의 entry에 대해 미분값이 W이므로 결과는 W에 h*w 승이 된다. (자세한 내용은 여기 블로그를 참고하면 될 것이다. )

결국 1x1 conv 의 inverse는 $\mathbf{W} ^{-1}$에 dependent하다. 이때 W의 크기가 상대적으로 작기 때문에(cxc) 충분히 계산할 수 있다.

하지만 여전히 연산량이 부담되기에 LU factorization을 이용해 연산량을 감소했다. 자세한 내용은 패스하겠다.

3) Affine coupling layer

앞서 봤던 RealNVP와 동일한 메커니즘이다.

RealNVP에서는 추가적으로 actnorm, 1*1 convolutional layer를 넣었으며 이 과정에서 전 단계가 invertible하게 만들기 위해서 여러 장치를 해뒀다고 생각하면 된다.

---

MintNet

MintNet은 2019년에 나온 모델로, M asked In vert ible Net work이다.
📄 paper: https://arxiv.org/pdf/1907.07945.pdf

가장 간단한 linear transformation은 다음과 같이 쓸 수 있는데,

이때 W는 triangular matrix여야 한다고 했다.

📌 왜 W는 triangular matrix여야 할까?

이전에 다른 모델에서 봤듯이, normalizing flow의 가장 중요한 점 중 하나는 transformation f 가 쉽게 invertible 하면서 Jacobian determinant 계산이 간단해야 했다.

위의 linear transformation은 당연히 invertible하다. 또, f(x)를 x에 대해 미분하면 W만 남을 것이고, 이게 바로 Jacobian matrix이기에 계산이 간단하기 위해선 triangular matrix여야 한다고 했다.

논문에서는 이러한 linear transformation + triangular Jacobian을 basic module 이라 부른다.

또, 여기서 한 가지 재미있는 사실을 보여준다.

바로 딥러닝에서 흔히 쓰이는 Convolution 도 이러한 linear transformation의 일종이라는 것이다. 사실 이 말이 직관적으로 바로 이해하긴 어렵다. 예시를 들어서 확인해보자.

우선 convolution을 linear transformation이라 부르기 위해선 convolution의 연산 결과값과 $y = \mathbf{L}x$의 결과값이 같아야 한다.

말이 어렵지 사실 되게 간단한 아이디어다.

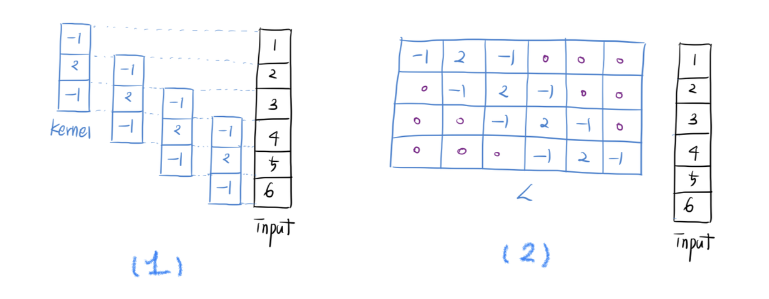
왼쪽 (1)은 1차원 kernel을 만들어 여느 때와 같이 sliding window 방식으로 convolution 계산을 하는 것이다. 그런데 생각해보면 이 길이 3짜리 kernel vector 를 matrix 로 표현할 수도 있다. 바로 오른쪽 (2) 그림이다.

input과 만나는 부분은 커널 내 값으로, 그 외에 부분은 0으로 채워넣는다. 이 상태에서 input 벡터와 곱하면 당연히 convolution을 계산한 (1)과 동일한 결과값이 나올 것이다. 따라서 Convolution 도 Linear Transformation 의 일종임이 증명되었다.

그럼 이러한 사실을 이용해서 MintNet이 어떻게 f를 만들었는지 보자.

1) Low Triangular Jacobian

📖 [Proposition 1]
Define $F$ as the set of all continuously differentiable functions whose Jacobian is lower triangular. Then F contains the basic module, and is closed under the following composition rules.

F를 Jacobian 이 low-triangular 이면서, 전체 연속이면서 미분 가능한 함수들의 집합이라 정의하자. 그렇다면 F는 아래 두 composition rule에 대해 닫혀있다.

1. Rule of Addition :
   $f_1 \in F\ \land \ f_2 \in F \implies \lambda f_1 + \mu f_2 \in F \ ,\text{where} \ \lambda, \ \mu \in \R$

2. Rule of Composition :

   $f_1 \in F\ \land\ f_2 \in F \implies f_2 \circ f_1 \in F$

특별 케이스로 $f \in F \implies h \circ f \in F$ 가 성립한다. 이때 $h(\cdot )$는 element-wise로 계산하는 미분 가능한 non-linear univariate 함수이다.

두 번째 rule을 보면 미분 가능한 univariate 함수 $h$에 대해 합성해도 여전히 미분 가능하다고 했다. 여기서 univariate 함수는 값을 하나만 받는 함수로 $y=x^3$와 같은 애들을 말한다.

Deep Learning에서 사용되는 activation 함수도 여기에 속한다. element-wise 하게 계산하는 activation 함수는 univariate 함수이기 때문에. 하지만 모든 activation 함수가 다 포함되는 것은 아니다. 가장 대표적인 예시로 ReLU 는 미분 불가능점이 있기 때문에 여기서 예외다.

📌 참고로 activation function을 포함한 univariate function은 Jacobian이 대각 행렬 이다. 왜냐면 하나의 값에만 관련이 있기 때문에 다른 변수에 대해 미분값이 0이 된다. 따라서 당연히 triangular matrix 조건도 만족한다.

자세한 수식 풀이는 논문을 참고하면 좋을 것 같다.

여튼 위의 proposition 1에서 제안한 두 가지 연산을 반복적으로 적용하면 우리는 basic module로 부터 복잡하고 non linear 한 module을 얻을 수 있다. 물론 continuous와 triangular Jacobian 성질은 유지하면서 말이다.

한 가지가 걸린다.

앞에서도 recap했지만 Normalizing Flow의 f에는 두 가지 조건이 있다.

1. Easily Invertible
2. Easily Compute the Determinant of Jacobian

위 proposition 1으로 2번 조건은 만족했지만 여전히 가장 큰 문제가 남았다. 바로 1번 Invertible해야 한다는 것! 따라서 여기에 Theorem 1이 추가되었다.

2) Invertibility

📖 [Theorem 1]
If 𝑓 ∈ ℱ and 𝐽𝑓(𝐱) is non-singular for all 𝐱 in the domain, then 𝑓 is invertible.

함수 f의 Jacobian 행렬이 non-singular 하다면, 다른 말로 full rank 를 가지고 있다면 f는 invertible하다.

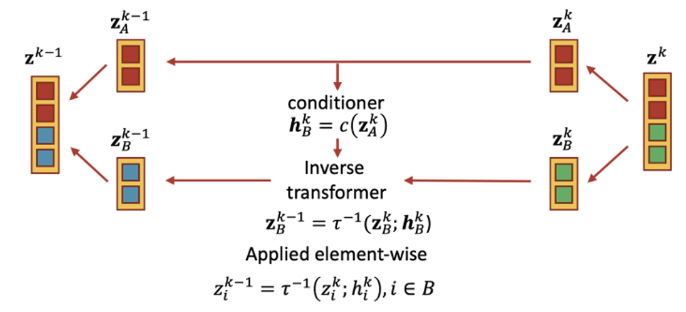
아래 다이어그램으로 보면 Generative model들의 제약 조건과 그에 따른 표현력을 나타내는 그림이다.

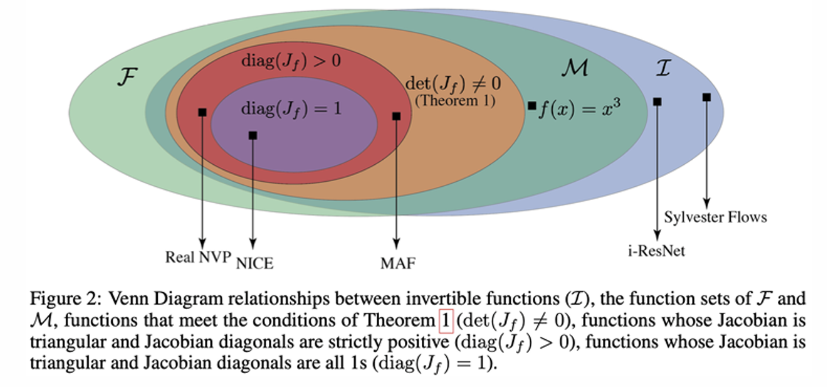
처음으로 봤던 NICE는 det(J) = 1인 가장 제한적인 모델이었다. 또, RealNVP는 diag(J) > 0로 확장했다. 이 두 모델 다 위에서 본 theorem 1에 속한다. 즉, MintNet은 diag(J) ≠ 0으로, 이 중에서 가장 확장된 버전이다.

참고로 theorem 1같은 경우에 역은 성립하지 않는다. singular 하면, 다시 말해 det(J) != 0 하면 invertible하는 것은 성립하지만, 역으로 invertible하다고 무조건 다 singular한 것은 아니다.

쉬운 예시로 $f(x) = x^3$을 보면 invertible하지만 det(J)=0이다. x=0일 때 미분값이 0이기 때문에! 따라서 이 함수는 MintNet에서 사용할 수 없다.

위 다이어그램을 통해 “표현력”도 알 수 있다. 제약이 덜 할수록 표현력은 더 커지게 된다. 가장 제약이 많은 NICE는 volume preserving의 제약으로 인해 표현력이 매우 제한된다. 그에 비해 MintNet은 det(J) ≠ 0이면 되기 때문에 더 좋은 표현력을 가지고 있다.

Architecture

그럼 이제 MintNet의 아키텍처를 보자. 상세하게 보진 않고 좀 눈여겨볼 만한 것들을 중심으로 간단히 정리해보겠다.

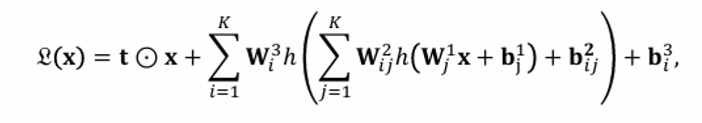
이게 바로 invertible 하면서 triangular Jacobian 을 가진 MintLayer이다.

보면 linear transformation을 여러번 합성한 것을 통해 전체가 $f \in F$라는 사실을 proposition 1을 통해 알 수 있다.

또, h는 invertible + low triangular Jacobian을 가진 activation function을 사용했다. (e.g. ELU, tanh, sigmoid)

MintNet에서는 더 표현력이 좋은 네트워크로 만들기 위해 다음 두 설정을 덧붙였다.

(1) Paired two Mint Layers

Mint Layer의 jacobian은 low triangular 를 가지도록 제한하고 있기 때문에 당연히 그 capacity도 제약이 생긴다. 또, low triangular만 사용하면 mask conv를 하는 과정에서 blind spots이 생길 수 있다는 문제점이 생긴다.

이를 해결하기 위해 Mint Layers를 두 개씩 페어로 묶어 하나를 upper 로, 다른 하나를 lower 로 사용하여 마치 full jacobian을 쓰는 듯한 효과를 준다.

(2) Squeezing layers

효과적으로 receptive field 를 넓히는 것은 중요하지만 이 과정에서 사용되는 subsampling 과정들(e.g. pooling, strided conv)은 invertible 하지 않다는 문제점이 있다. 따라서 이 논문에서는 대신에 squeezing 기법을 사용하여 해상도를 줄이면서 채널 수를 늘릴 수 있으며, 동시에 invertible하게 만든다.

그냥 tensor의 reshape으로 생각하면 될 것 같다

여기까지 총 네 가지의 모델들에 대해 간단히 알아봤다. 구체적인 내용보다는 개요 정도로 보면 될 것 같다. 각각의 모델에 대해 논문 링크를 걸어두었으니, 더 자세한 내용은 논문을 읽어보는게 가장 빠를 것이다. Normalizing flow는 여기까지:)