확률변수
확률변수 (Random Variable)
-
표본공간에서 각 사건에 실수를 대응시키는 함수를 확률 변수라고 함.
-
확률 변수의 값은 하나의 사건에 대하여 하나의 값을 가지며, 실험의 결과에 의하여 변함.
-
일반적으로 확률 번슈는 대문자로 표현하며, 확률 변수의 특정값을 소문자로 표현.
- 확률 변수 : X, Y 등 대문자 표현
- 확률 변수의 특정값 : x,y 등 소문자 표현
- 이산 확률 변수(Discrete random variable) : 셀 수 있는 값들로 구성되거나 일정 범위로 나타나는 겨웅
- 연속 확률 변수(continuous random variable) : 연속형 또는 무한대와 같이 셀 수 없는 경우
-
확률 변수 예시
(a) 반도체 1000개의 wafer 중 불량품의 수 X
(b) 공장에서 생산하는 전구의 수명 T
(c) 주사위를 던질 때 나오는 눈의 수 V
- 확률 변수의 평균 : 기대값이라고 표현하기도 하며, 수식은 아래와 같다.
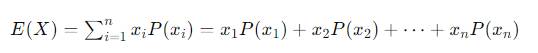
- 주사위를 던졌을때의 기대값은
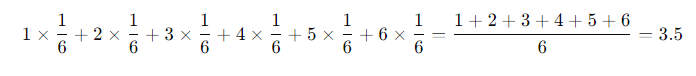
- 확률변수의 분산
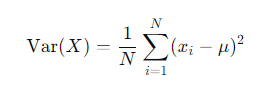
-
기대값의 성질 : a,b가 상수이고, X,Y를 임의의 확률 변수라고 할 때 다음이 성립
- E(a) = a
- E(aX) = aE(X)
- E(aX + b) = aE(X) + b
- E(aX ± bY) = aE(X) ± bE(Y)
- X,Y가 독릴일때, E(XY) = E(X) ⋅ E(Y)
- 분산의 성질 : a,b가 상수이고 X, Y를 임의의 확률 변수라고 할 때
- Var(a) = 0
- Var(aX) = a^2 ⋅ Var(X)
- Var(X+Y) = Var(X) + Var(Y) + 2Cov(X,Y)
- Var(aX ± bY) = a^2 ⋅ Var(X) ± b^2 ⋅ Var(Y) + 2Cov(X,Y)
- X, Y가 독립일때, Var(XY) = 0
- Var(X) = E(X^2) - [E(X)]^2
-
공분산
-
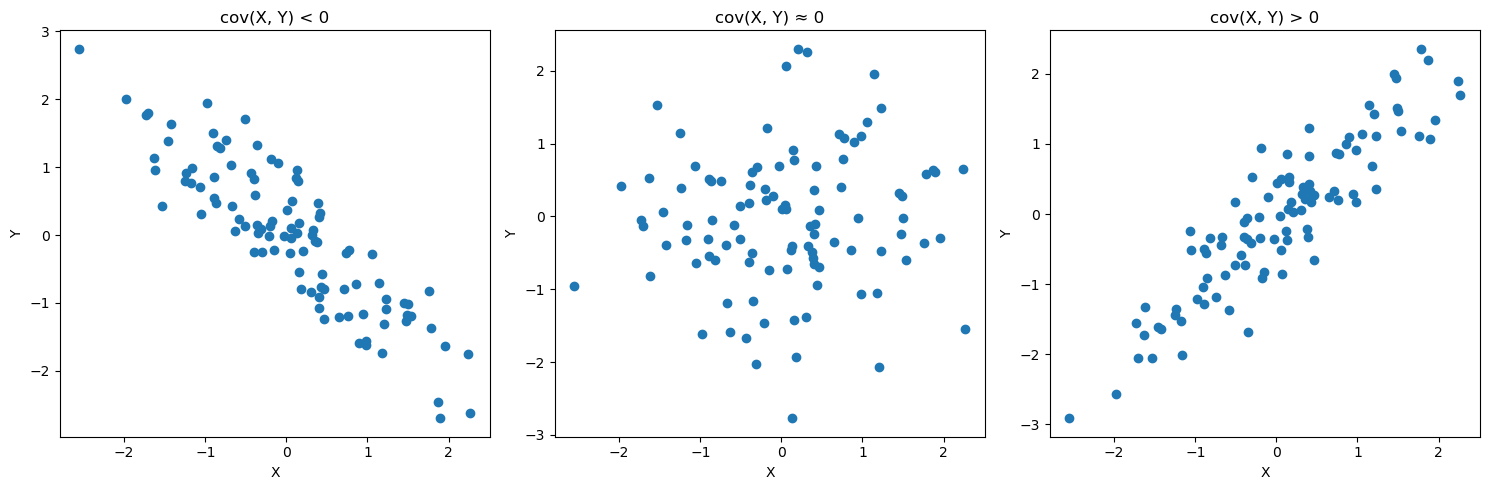
2개의 확률변수의 선형관계를 나타내는 값으로, 하나의 값이 상승할 때 다른 값도 상승한다면, 양의 공분산을 가지고 반대로 하나의 값이 상승할 때 하락한다면 음의 공분산을 가짐
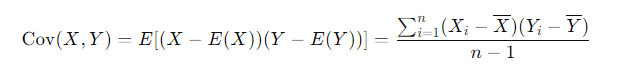
-
확률 분포
-
확률 변수 X가 취할 수 있는 모든 값과 그 값이 나타날 확률을 표현한 함수 (probability distribution)
-
확률 분포
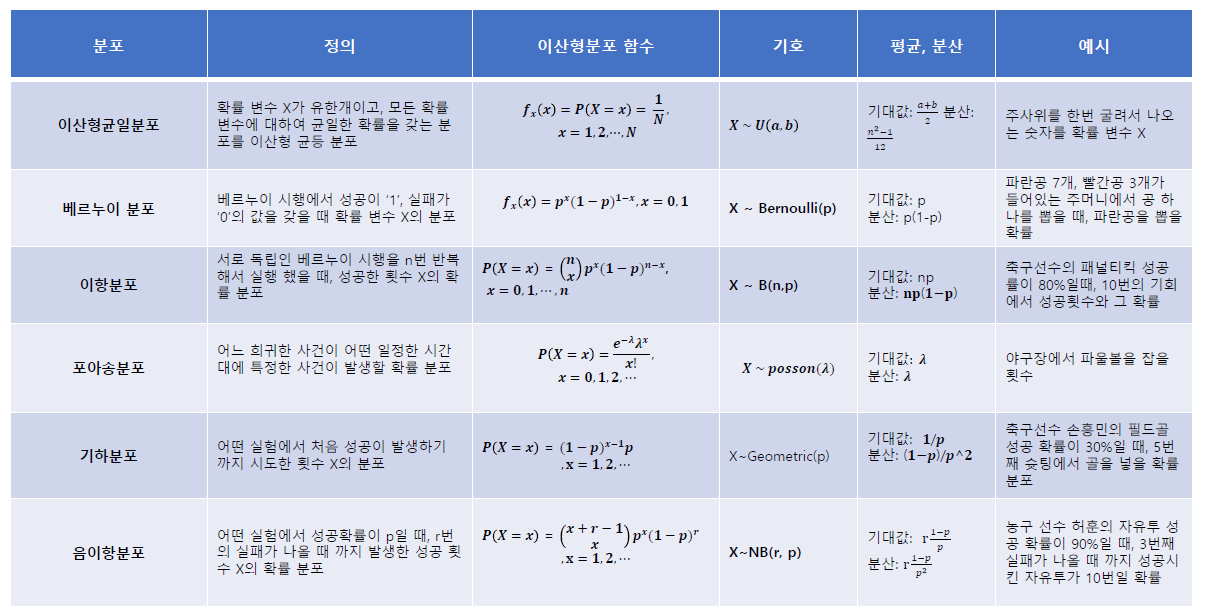
- 이산형 확률분포 : 베르누이분포, 이항분포, 포아송분포, 기하분포, 음이항분포, 초기하분포
- 연속형 확률분포 : 균일분포, 정규분포, 감아분포, 지수분포, 카이제곱분포, 베타분포
이산형 균등분포
- 이산형 균등 분포 (Discrete uniform distribution)
- 확률 변수 X가 유한개이고, 모든 확률 변수에 대하여 균일한 확률을 갖는 분포를 이산형 균등 분포라고 함
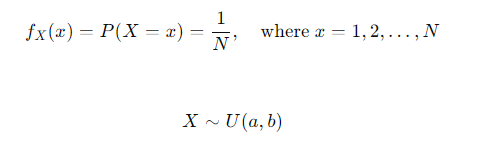
- 주사위를 한번 굴려서 나오는 숫자를 확률 변수 X라고 하면, 확룰 변수 X는 아래와 같다.
| X | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| f(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
- 이산형 균등분포의 기대값
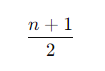
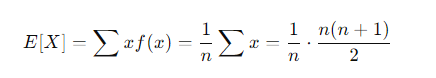
- 이산형 균등분포의 분산
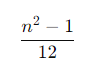
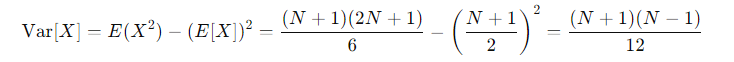
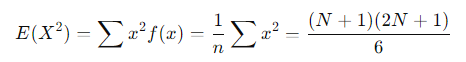
베르누이 분포
- 베르누이 시행(Bernoulli trial) : 각 시행의 결과가 성공, 실패 두 가지 결과만 존재하는 시행을 베르누이 시행이라고 함
- 베르누이 시행은 성공이 1 실패가 0의 값을 갖을 때 확률 변수 X의 분포를
베르누이 분포(Bernoulli distribution)이라고 한다.
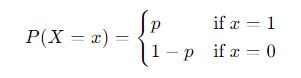
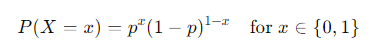
-
베르누이 분포의 평균 : p
- 기대값 E[X] = 1⋅p + 0⋅(1-p) = p
-
베르누이 분포의 분산 : p(1-p)
- 분산 Var[X] = E(X-p)^2 = (0-p)^2 ⋅ (1-p) + (1-p)^2⋅p = p⋅(1-p)
이항분포
- 이항분포(Binomial distribution) : 연속적인 베르누이 시행을 거쳐 나타나는 확률 분포
- 서로 독립인 베르누이 시행을 n번 반복해서 실행 했을 때, 성공한 횟수 X의 확률 분포
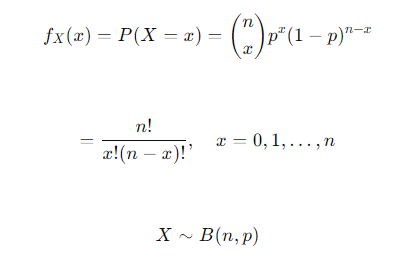
-
이항분포의 기대값 : np
-
이항분포의 분산 : np(1-p)
예제) 반도체 공장에서 불량이 발생할 확률이 10%라고 하면, 10개의 제품을 생성했을 때 불량이 2개 이하일 확률을 구하시오.
풀이) P(X≤2) = P(X = 0) + P(X = 1) + P(X = 2)
= 10C0 X (0.1)^0 X (0.9)^(10-0) + 10C1 X (0.1)^1 X (0.9)^(10-1) + 10C2 X (0.1)^2 X (0.9)^(10-2)
= 0.35 + 0.39 + 0.19 = 0.93
포아송 분포
-
포아송 분포(Poisson distribution) : 어느 희귀한 사건이 어떤 일정한 시간대에 특정한 사건이 발생할 확률 분포
-
포아송 분포의 조건
- 어떤 단위구간 (1일 등)동안 이를 더 짧은 작은 단위의 구간(1시간 등)으로 나눌 수 있고 이러한 더 짧은 단위구간 중에 어떤 사건이 발생할 확률은 전체 척도 중에서 항상 일정
- 두 개 이상의 사건이 동시에 발생할 확률은 0에 가까움
- 어떤 단위구간의 사건의 발생은 다른 단위구간의 발생으로부터 독립적임
- 특정 구간에서의 사건 발생확률은 그 구간의 크기에 비례함
- 포아송분포 확률 변수의 기댓값과 분산은 모두 λ 임
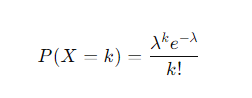
- λ = 단위시간 또는 단위공간에서 발생하는 평균 사건의 수
- k = 사건의 수
- e = 자연상수 (약 2.71828)
- k! 는 k의 factorial
이항 분포의 포아송 근사
- 확률 변수 X가 X ~ B(n,p)이고, n이 충분히 크고, p가 아주 작을 때, X의 분포는 평균이 λ=np 인 포아송 분포로 근사시킬 수 있음.
- 보통 n이 클 때, np<5를 만족하게 p가 작으면 근사 정도가 좋다고 함. X ~ poisson(np)
기하분포
- 기하분포(geometric distribution) : 어떤 실험에서 처음 성공이 발생하기까지 시도한 횟수 X의 분포. 이 때 각 시도는 베르누이 시행을 따름.
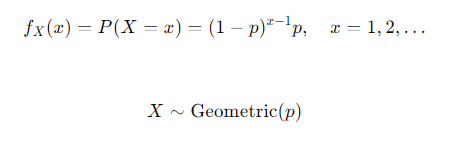
- 기하분포의 기대값 = 1/p
- 기하분포의 분산 = (1-p)/p^2
음이항분포
- 음이항분포 (negative binomial distribution) : 어떤 실험에서 성공확률이 p일 때, r번의 실패가 나올 때 까지 발생한 성공 횟수 X의 확률 분포
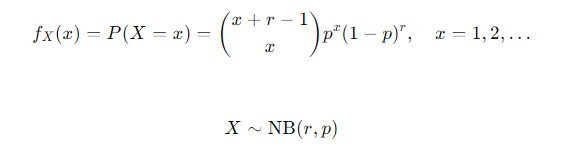
- 기대값 : r × (1-p)/p
- 분산 : r × (1-p)/p^2
Summary