
연속형 확률 분포
확률밀도함수(pdf)
- 확률밀도함수 (probability density function) : 연속형 확률 변수 X에 대하여 함수 f(x)가 아래의 조건을 만족하면, 확률밀도함수라고 함.
누적분포함수(cdf)
- 누적분포함수(Cumulative density function) : 확률밀도함수를 적분하면 누적분포함수가 됨.
균일분포
- 균일분포 (uniform distribution) : 확률 변수 X가 a와 b사이에서 아래와 같은 확률 밀도 함수(pdf)도 같음.
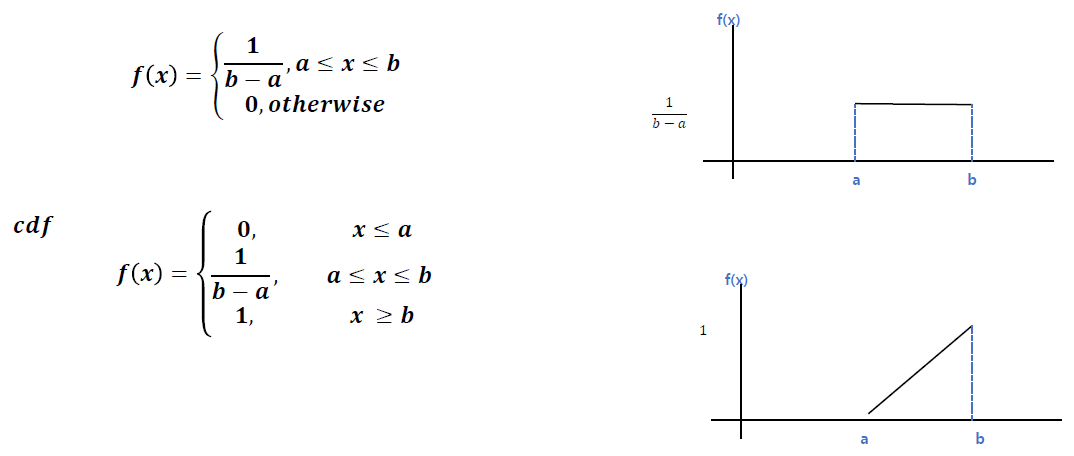
정규분포
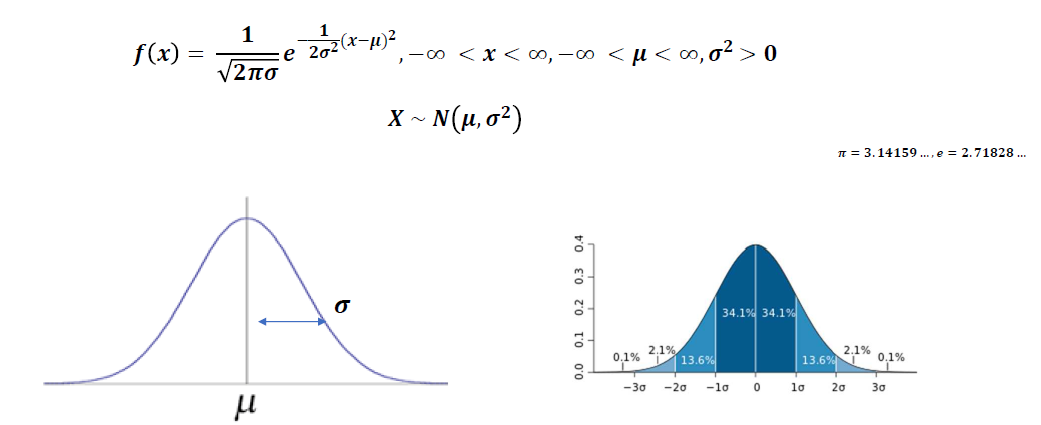
- 정규 분포 (normal distribution)
- 19세기 최대 수학자라고 불리는 독일의 가우스에 의해 제시된 것으로 가우스 분포라고도 함
- 확률 밀도 함수는 확률 변수 X가 평균이 μ이고, 분산이 σ^2인 정규분포를 따를 때 아래와 같다.
표준 정규 분포
-
표준 정규 분포 (standard normal distribution)
-
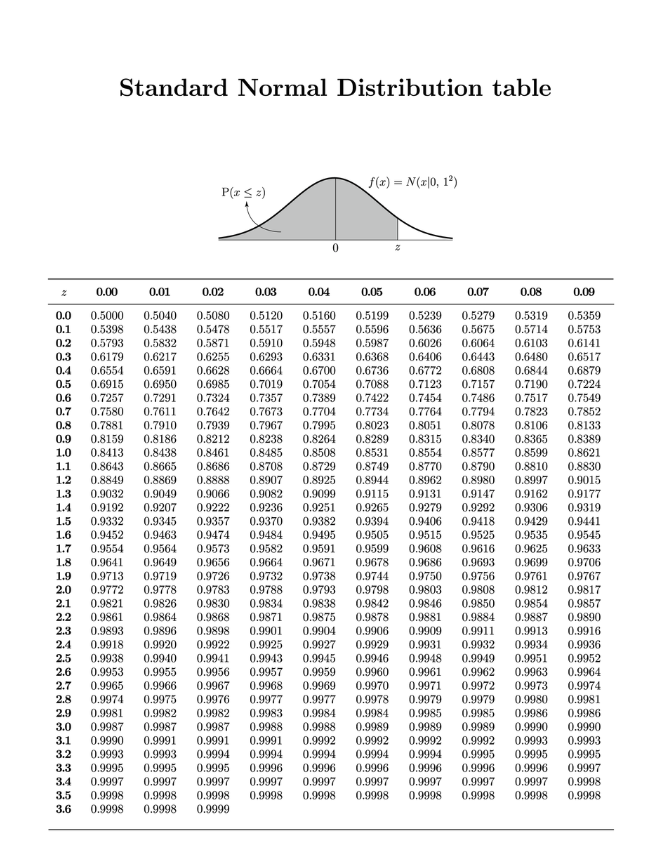
확률 변수 X~N(μ, σ^2) 정규분포를 따르고, 확률 변수 Z = (X-μ)/σ 할 때 확률 변수 Z~N(0,1)
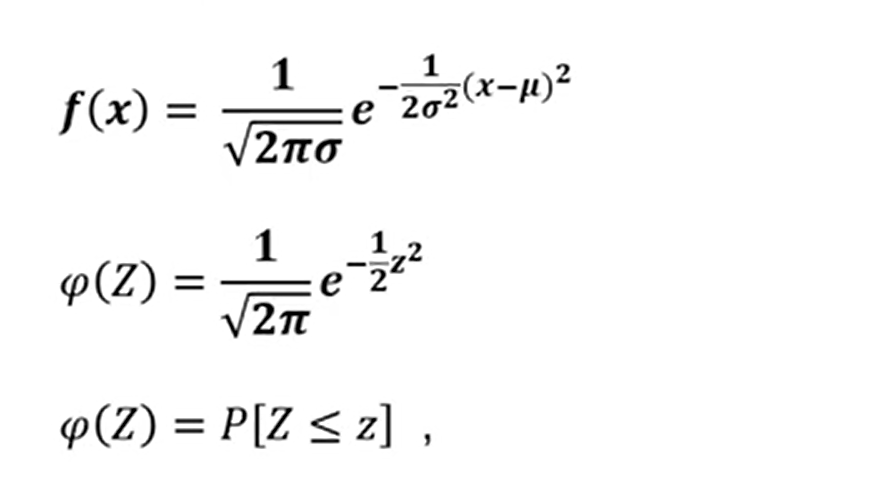
이항분포의 정규 근사
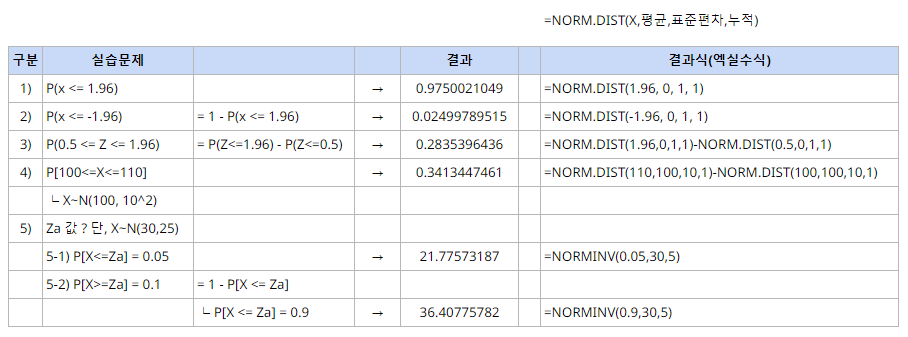
연속형 확률 분포 실습
지수분포
-
지수분포(exponential distribution) : 단위 시간당 발생할 확률 λ인 어떤 사건의 횟수가 포아송 분포를 따른다면, 어떤 사건이 처음 발생할때까지 걸린 시간 확률 변수 X는 지수분포임.
-
예시) 버스 정류장에서 100번 버스가 도착하는 횟수가 포아송 분포를 따른다면, 첫 번째 버스가 도착할 때까지 대기 시간의 분포가 지수분포임
-
지수분포의 PDF

- 지수분포의 CDF

-
지수분포의 평균 : E[X] = 1/λ
-
분산 : Var[X] = 1/λ²

지수분포의 무기억성
-
어떤 시점부터 소요되는 시간은 과거 시간에 영향을 받지 않음
-
지수분포의 무기억성(property of memorylessness)은 중요한 특성 중 하나로, 이는 특정 시점까지 경과한 시간이 이후에 발생할 사건의 확률에 영향을 주지 않는다는 의미입니다. 즉, 사건이 발생하는 데 걸리는 시간이 이미 얼마나 경과했는지와 무관하게 항상 동일한 확률을 갖는다는 뜻입니다.


예시)
예를 들어, 특정 시스템의 고장이 지수분포를 따른다고 가정할 때, 이 시스템이 지난 10시간 동안 고장 나지 않았다고 해서 앞으로 고장이 날 때까지 걸리는 시간의 분포가 변하지 않는다는 뜻입니다. 다시 말해, 이미 10시간이 경과한 후에도 앞으로 5시간 동안 고장 나지 않을 확률은 처음부터 5시간 동안 고장 나지 않을 확률과 동일합니다.
이 특성은 실용적인 응용에서 매우 유용합니다. 예를 들어, 고객 도착 시간, 장비 고장 간격, 통신 시스템의 패킷 도착 시간 등을 모델링할 때 지수분포의 무기억성 특성이 유용하게 사용됩니다.
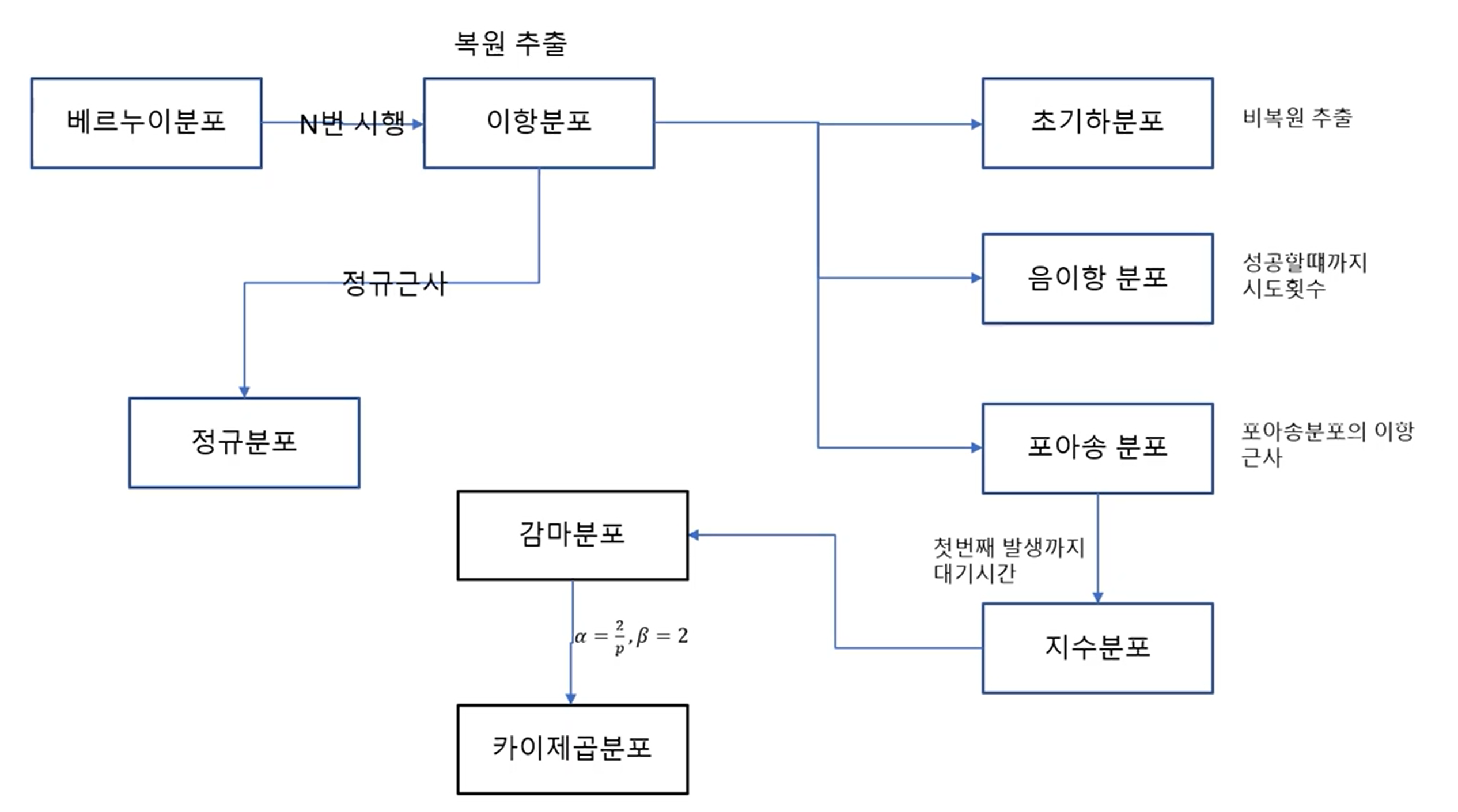
확률 분포의 관계도
모집단과 표본 분포
모집단, 표본
- 모집단 (Population), 표본(Sample)
- 모집단 : 전체 집단을 나타내며, 큰 원으로 표현됩니다.
- 표본 : 모집단에서 선택된 일부 집단으로, 모집단 내부의 작은 원 또는 여러 개의 점으로 나타낼 수 있습니다.
| 구 분 | 모집단 | 표본 |
|---|---|---|
| 평균 | μ | X ̄ |
| 분산 | σ² | s² |
표본추출
-
표본추출(Sampling) : 모집단으로부터 표본을 추출하는 것을 Sampling이라고 하며, 표본으로부터 그 특성을 찾아내고 모집단의 특성을 추론하고자 함
-
모집단에서 표본을 추출하는 방법에는 여러가지가 있음
- 복원추출 (Sampling with replacement) : 모집단에서 데이터를 추출 할 때 하나를 추출하고 다시 넣고 추출하는 방법으로 동일한 표본이 추출 될 수 있음
- 비복원추출 (Sampling without replacement) : 모집단에서 데이터를 추출 할 때 하나를 추출하고 다시 넣지 않고 추출하는 방법
- Random Sampling : 모집단에서 데이터를 추출할 때 주의할 점은 편향되지 않아야 함, 각 개체가 모두 동일한 확률로 추출하는 방법
불균형 데이터
- 불균형 데이터(Imbalanced Data)의 문제
- 데이터가 불균형 데이터일 경우 문제가 생김
- 우리가 예측모형을 만드는 목적은 관심이 있는 대상이 발생할 확률을 예측하는 경우가 대부분임. 그런데 예측대상이 전체 대비 아주 낮다면? → 모형의 성능이 괜찮을까? (ex. 신용평가 모형개발, 제조불량예측 등)
1) Sampling 기법을 통하여 해결
2) 모델을 통한 성능 개선 (ex. Cost-sensitive learning)
Sampling 기법
-
관심의 대상이 아주 낮은 비율일 경우
-
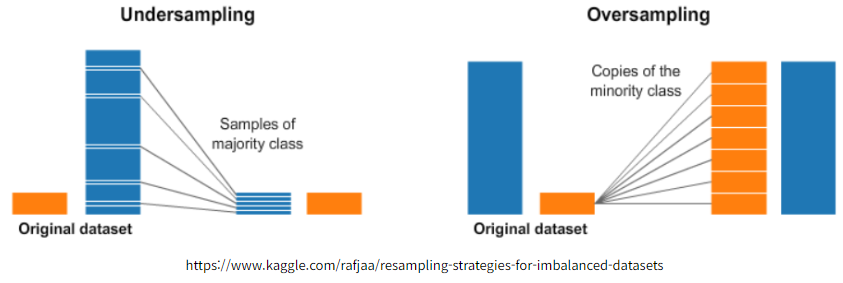
Over Sampling
- 타켓 데이터의 적은 class의 수를 많은 class의 비율만큼 증가시킴 (일정 비율로 복원추출하는 개념)
- 과도적합의 문제 발생 가능
- Under Sampling
- 타켓 데이터의 많은 class의 수를 적은 class의 비율만큼 감소 시킴
- 임의로 뽑은 데이터가 biased(편향)될 수 있고, 모형의 성능이 떨어질 수 있음
표본분포
통계량
- 통계량 (Statistic) : 표본에 기초하여 계산되는 수치 함수를 통계량이라고 함.
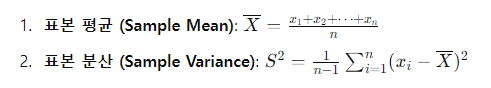
-
표본분포 (Sampling distribution) : 통계량들이 이룬느 분포를 표본분포라고 함
-
표본 평균 (Sample mean)
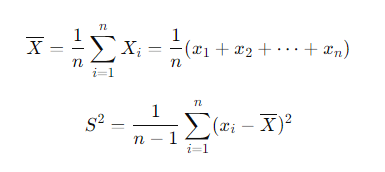
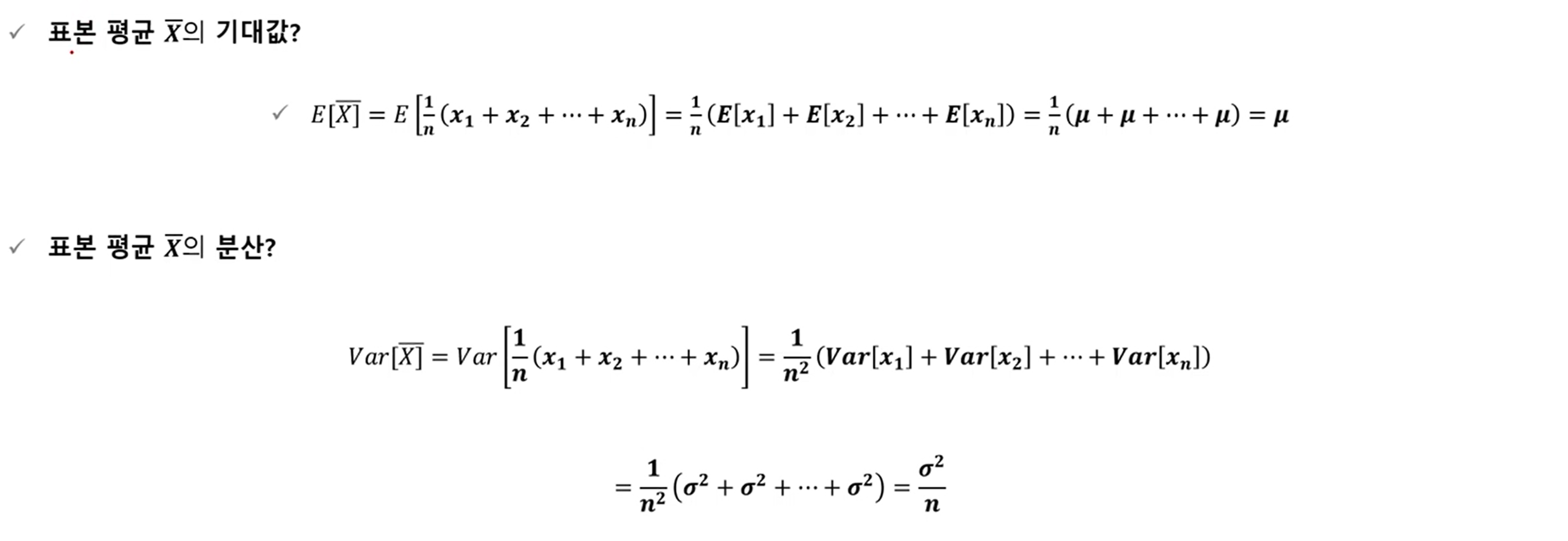

중심극한 정리
- 중심극한 정리 (Central limit theorem) : 평균이 μ이고 분산이 σ²인 임의의 모집단에서 랜덤 표본 X1, X2, ... Xn을 추출할 때 표본의 크기 n이 충분히 (n ≥ 30) 크면, 표본 평균 X(bar)는 근사적으로 정규분포 N(μ,σ²/n)을 따른다
카이제곱분포
-
카이제곱 분포 (Chai-square distribution) : 확률 변수 Z1, Z2, ..., Zn 가 표준정규분포를 따른다면, 확률변수 Z는 Z1 + Z2 + ... Zn
-
Z ~ X²(n), Z 가 카이제곱 분포를 따를 때,

-
E[X] = v, Var[X] = 2v
-
자유도 (degree of freedom) : 표본수 - 제약조건의 수 또는 표본수 - 추정해야 하는 모수의 수를 의미하며 일반적으로 n-1을 사용
-
카이제곱 분포는 자유도 v의 크기에 따라 모양이 달라짐, 자유도가 커질수록 분포가 좌우 대칭 형태로 됨
-
카이제곱 분 포는 자유도가 커지면서 표준정규 분포에 근사하며, v≥30 이면, 확률을 근사적으로 정규분포로 구할 수 있음
T 분포
Tableau이후 작성