2025.01.02
Part.10 딥러닝
Chapter 02.Deep learning from Scratch
09. DL from scratch - 순방향 연산10. DL from scratch - 간단한 학습 원리11. DL from scratch - 오차의 역전파12. DL from scratch - 크로스엔트로피
Chapter 02. Deep learning from scratch
09. 순방향 연산
이번 강의는 딥러닝을 쌩으로 이해하기 이다. TensorFlow나 Pytorch 같은 프레임워크를 사용하지 않고 딥러닝을 해보면서 이해하는 시간.
순방향 연산... 하는 것을 통상
추론이라고 한다.
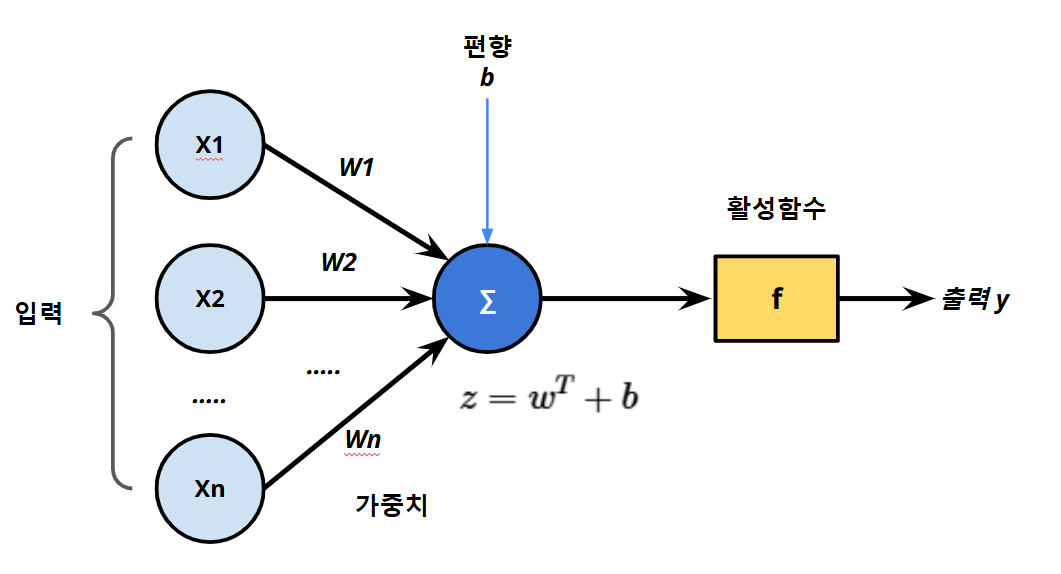
입력을 주고, 출력을 관찬하는 것이 추론, 순방향 연산
데이터 생성
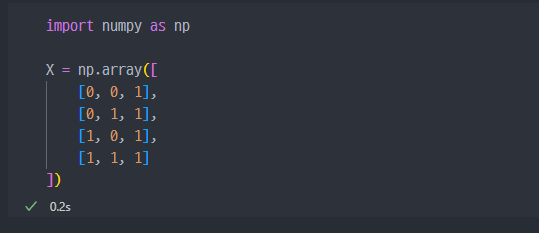
실습할 데이터 생성
Sigmoid 함수란?
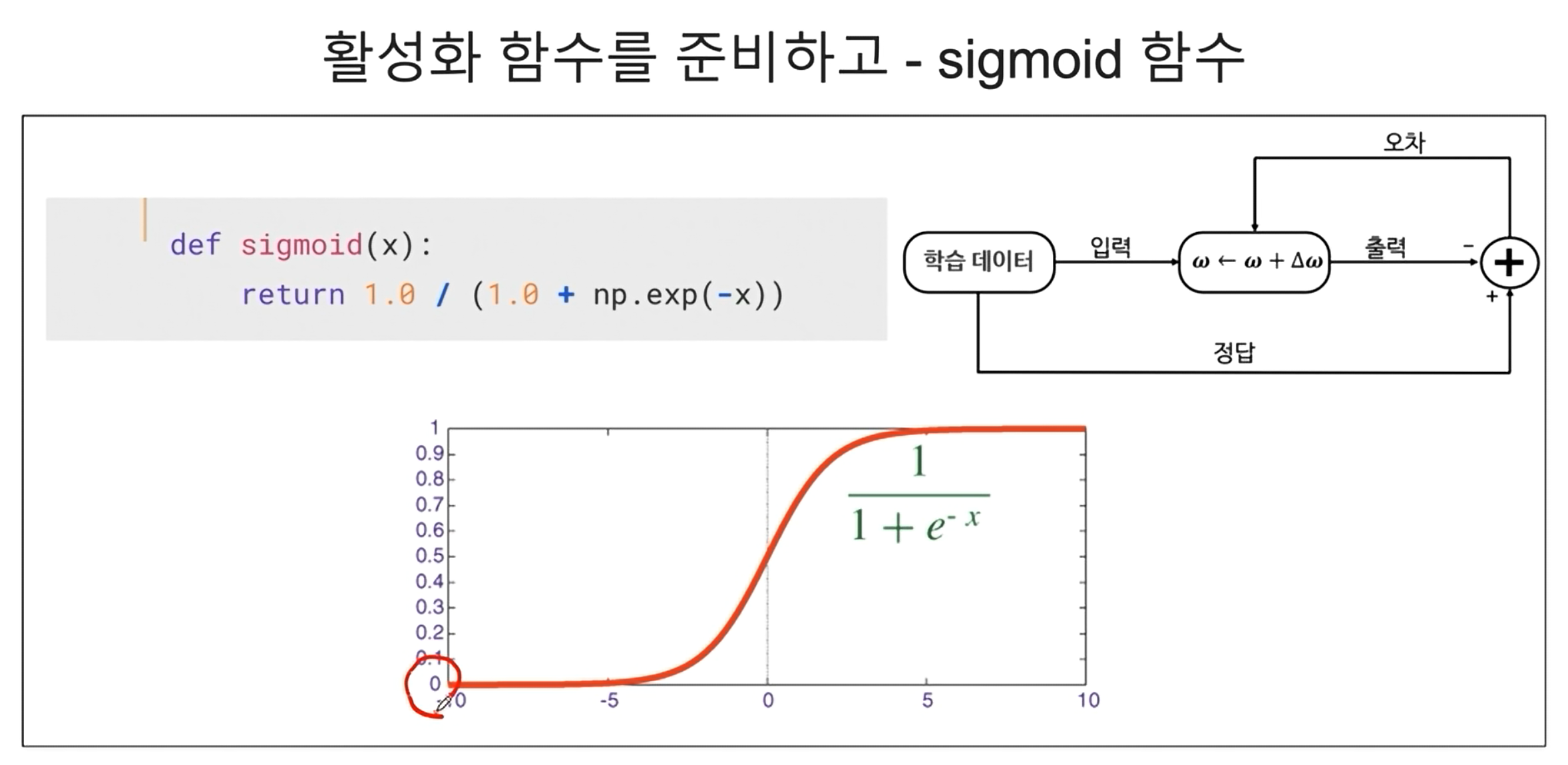
Sigmoid함수 생성
※ Sigmoid 함수에 대한 기초설명
시그모이드 함수는 S자형 곡선 또는 시그모이드 곡선을 갖는 수학 함수이다. 시그모이드 함수의 예시로는 첫 번째 그림에 표시된 로지스틱 함수가 있으며 다음 수식으로 정의된다. (e 는 자연상수 2.71828... 이다)

시그모이드 함수의 특징
출력 범위: 시그모이드 함수의 출력값은 항상 0과 1 사이입니다. 이 특성 때문에 이 함수는 확률을 나타내는 데에 아주 적합합니다.S자 곡선: 시그모이드 함수는 S자 형태의 곡선을 그립니다. 이 곡선은 부드러운 미분 가능한 형태를 가지고 있어서 최적화가 용이합니다.이진 분류: 로지스틱 회귀에서는 시그모이드 함수를 사용하여, 주어진 입력값이 특정 클래스에 속할 확률을 계산합니다. 이를 통해 이진 분류 문제를 해결할 수 있습니다.
활성화 함수의 종류
- 활성화 함수란?
기본적으로입력 신호의 총합을출력 신호로 변환하는 함수를 일반적으로 활성화 함수라 한다.
신경망을 구성하는데는 기본적으로 비선형 함수를 사용해야 한다. 그래야layer를 쌓는 의미가 있다.
1차 함수, 즉 선형함수를 사용하게 되면, 여러 개의layer를 쌓아도 결국 1차 함수이다.
예를 들어 라는 함수를 여러겹 쌓아서 를 하여도 결국
이처럼 선형함수를 이용하면 은닉층,layer의 효과를 살릴 수 없기에 비선형 함수를 사용해야 한다.
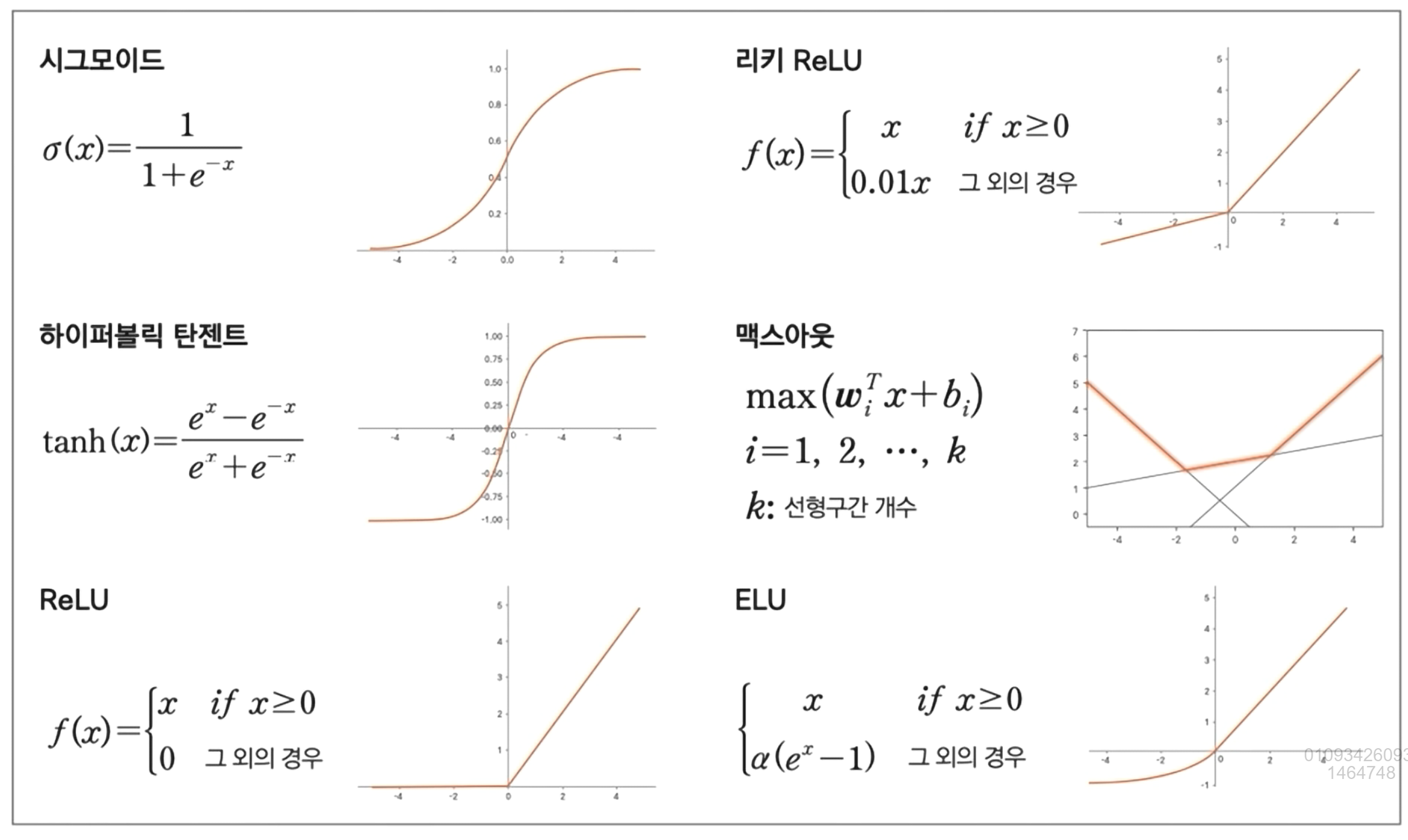
- 0과 1사이 값으로 출력이 나오는
sigmoid함수 - 그 다음 많이 사용하는 것이
ReLu함수, 가 0보다 클때는 작을때는 0 - 하이퍼볼릭 탄젠트는 시그모이드와 비슷하지만, -1에서 1 사이 값을 출력값으로 가진다.
통상 Sigmoid와 ReLu를 많이 사용한다.
가중치
가중치를 랜덤하게 선택. 원래는 학습이 완료된 가중치를 사용해야 한다.
입력값이 3개이면, 각각의 3개의 입력값마다 w 값 (가중치, 기울기)가 있어야 한다.
일단 학습 전이기에 랜덤하게 가중치를 생성한다.
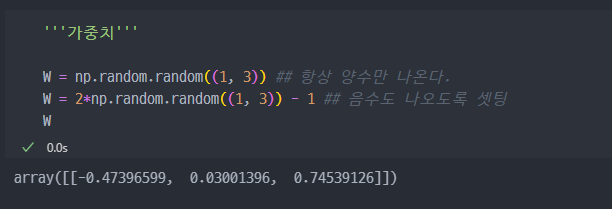
추론 결과
추론은 어떻게 하나? 하였을 때, w(가중치)와 x(입력)을 곱하면 된다.
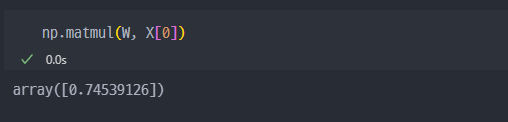
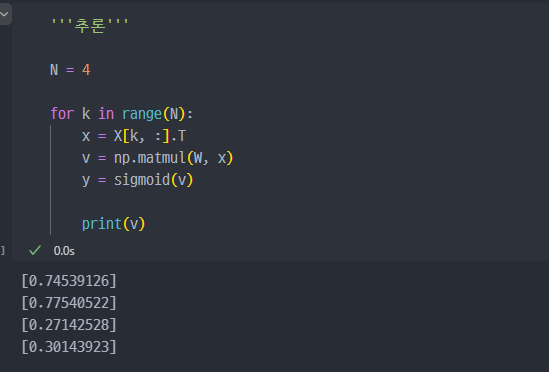
기존에
X에 저장되어 있는 4개의 데이터 (4개의 행)에서 각각의 3개의 컬럼값이 각각 가중치(w)와 곱해진 결과이다.
즉, 이게 순반향 연산을 한 것이다. 단, 가중치가 학습된 값이 아닌 기본랜덤값이므로 현재 의미는 없다.
10. 간단한 학습 원리
가중치 학습
가중치가 이제 정답을 맞추도록 학습을 진행해야 한다.
다만, 어떻게 학습을 시켜야할까?... → 지도학습이다. 즉 정답을 알려줘야 한다.
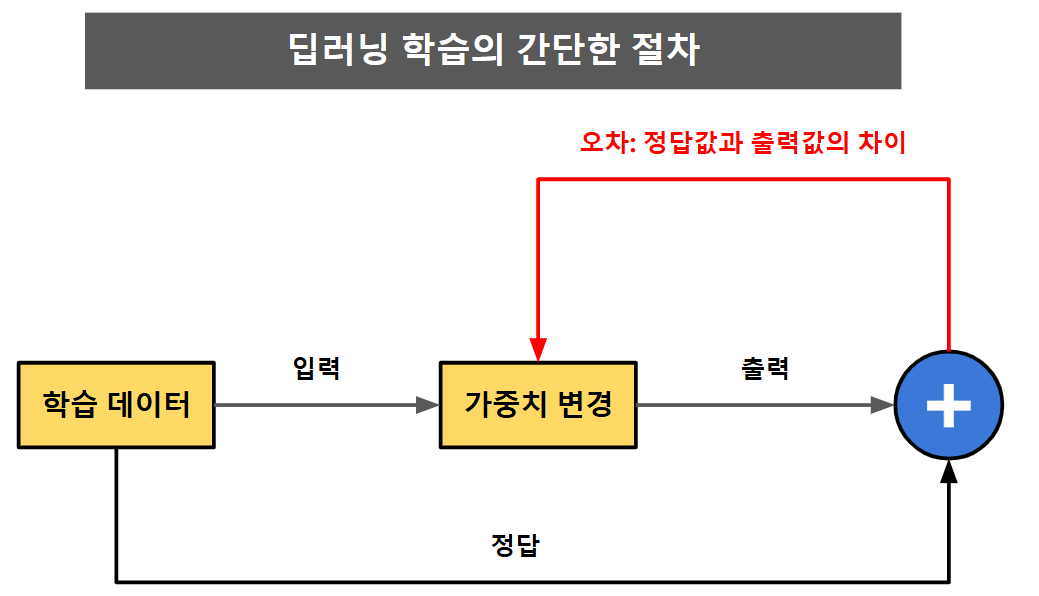
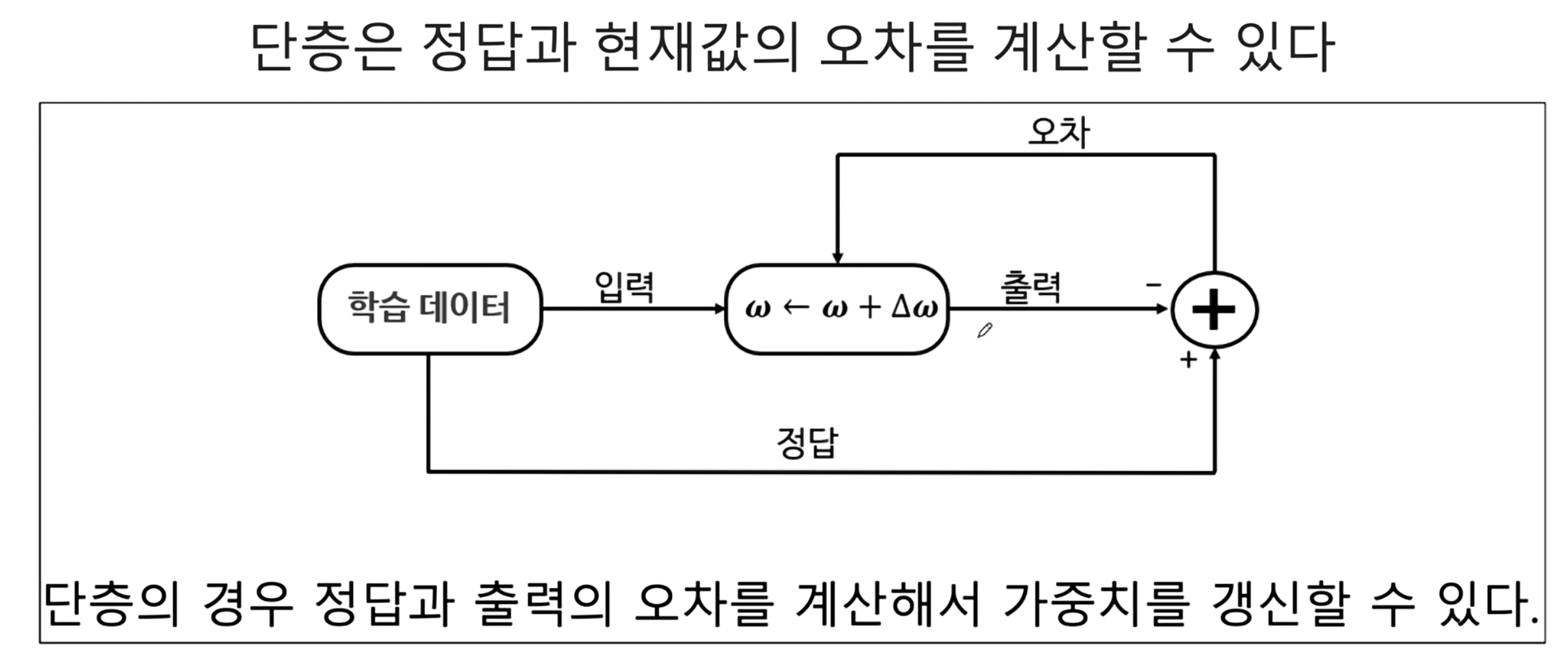
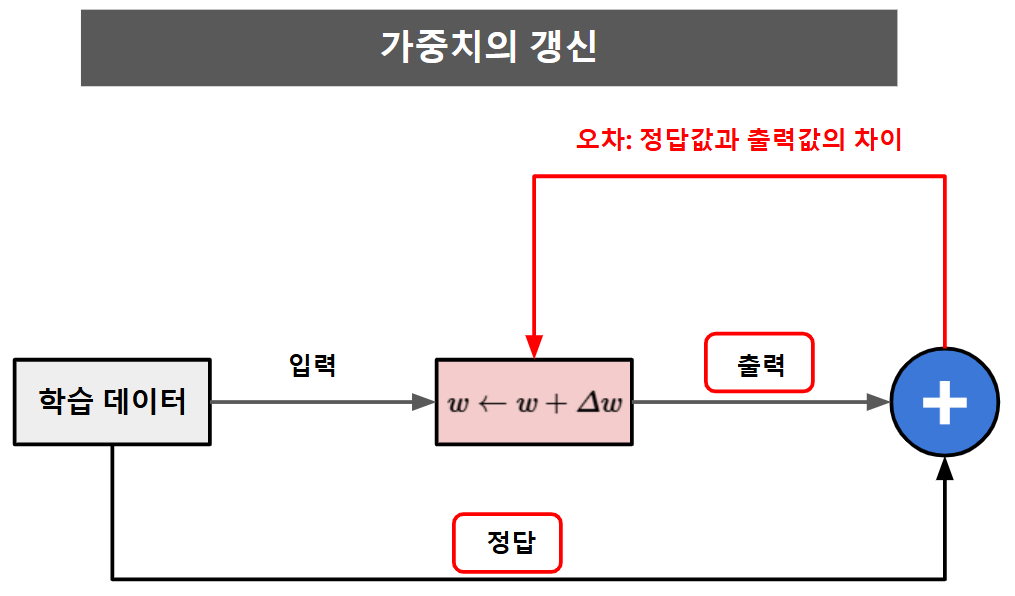
결국 정답값과 출력값의
차이, 즉 오차를 확인하고 이를 이용하여 가중치를 변경한다.
그렇다면... 가중치를 어떻게 변경(갱신) 하는것인가 ?
실습
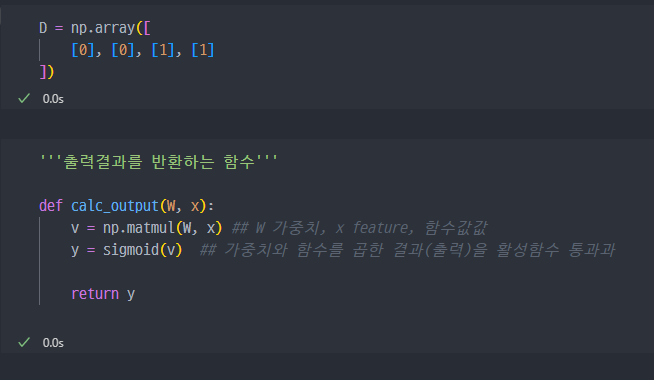
라벨값과 순방향 연산을 통해서
output을 출력하는 함수 생성
오차계산
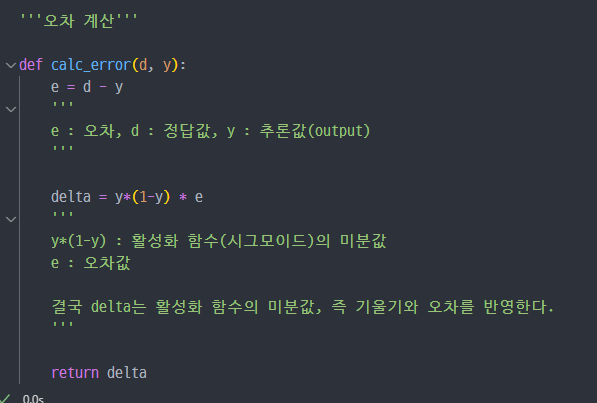
- 오차는 정답값 - 추론값(
output) 이다.- 다만 가 되기 위해선, 단순 오차만 반영하지 않고 활성화 함수의 미분값도 같이 반영한다.
- 따라서
delta는 을오차로 본다.
- sigmoid 함수의 미분값, 즉 기울기

한 epoch에 수행되는 W 계산
Gradient descent
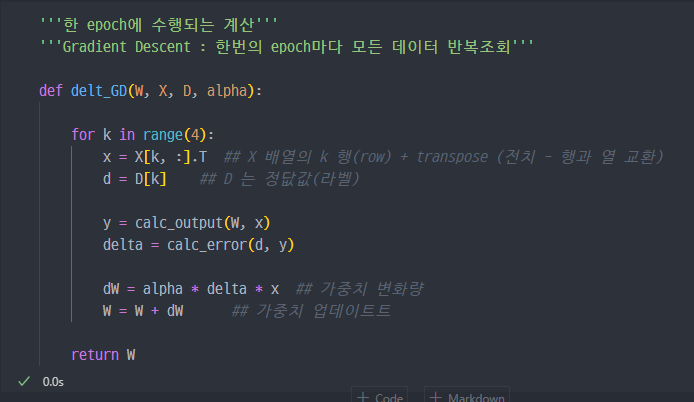
가중치를 랜덤하게 초기화하고 학습 시작
W→ 가중치(랜덤설정),D→ 라벨값(정답값),X→ Test 데이터, feature 값
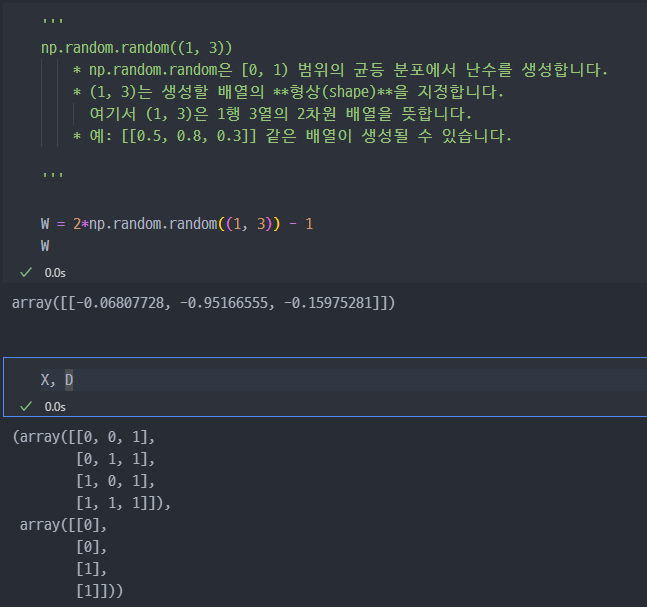
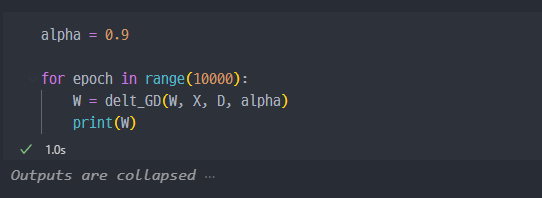
출력결과
최종 학습 결과 확인
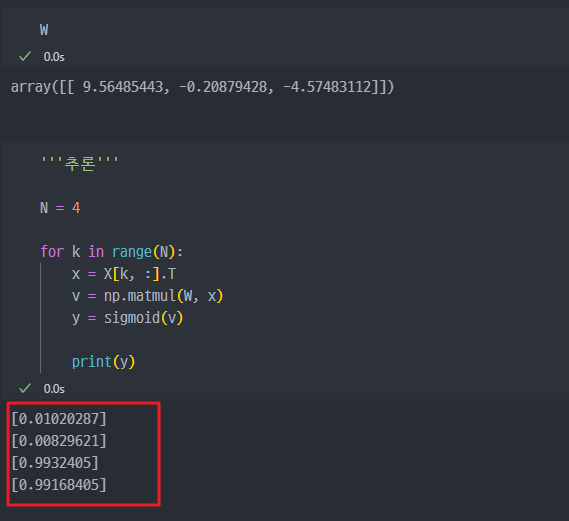
결과를 보면, 정답값 ( 0, 0, 1, 1) 과 거의 유사한 것을 볼 수 있다.
11. 오차의 역전파
XOR
앞선 강의와 마찬가지로 동일하게 계산진행해본다. W, D, X 설정하고 진행.
일단, X, D(라벨)값 설정하고, W 가중치는 랜덤하세 초기화 진행.
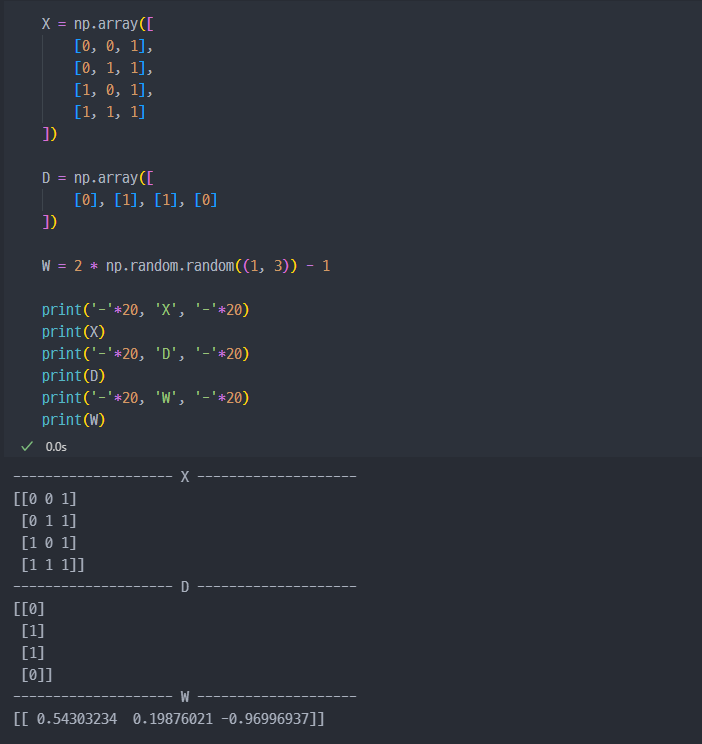
위와 동일하게
epoch10000번 진행해서 가중치(W) 학습하고, 추론진행(결과도출)해보니
정답값(0, 1, 1, 0)과 완전히 다른 값이 나온다.
다시보는 역사
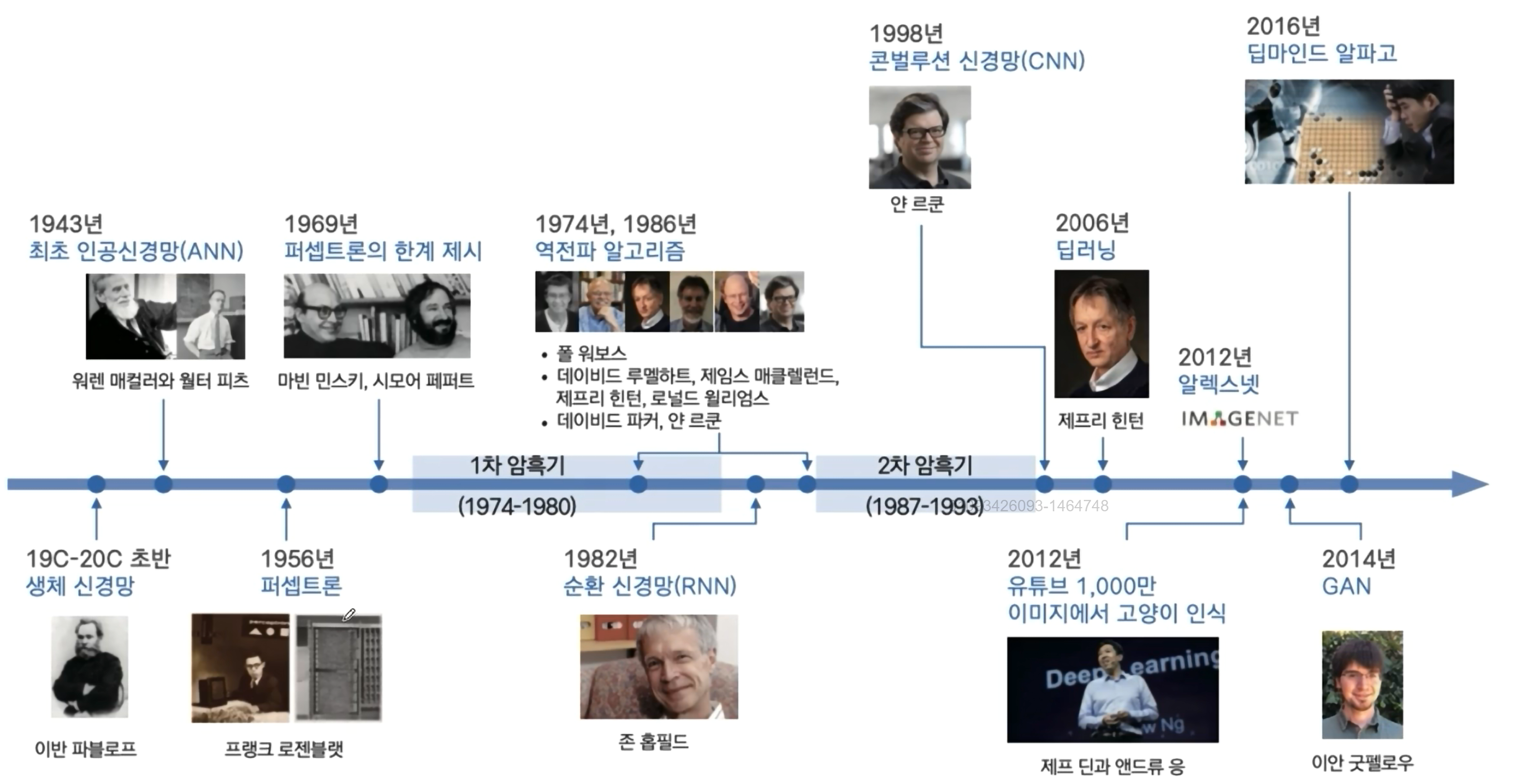
1956년에 퍼셉트론이 등장하였지만, 1969년에 퍼셉트론의 한계가 제시되면서, 1차 암흑기에 들어갔다.
그 한계는 XOR 같은 문제를 해결하기 위해선, 직선이 아닌 곡선(비선형)이 필요한데.. 퍼셉트론으로는 불가능 했기 때문이다. 퍼셉트론은 결국 데이터를 분리하는 방법이 직선(선형 결정 경계)이므로 선형 분리가 불가능한 XOR 같은 문제는 해결할 수가 없었던 것이다.
아래와 같이, 파란색과 붉은색의 데이터를 완벽하게 구분하기 위해선... 하나의 직선으로는 불가능하다.
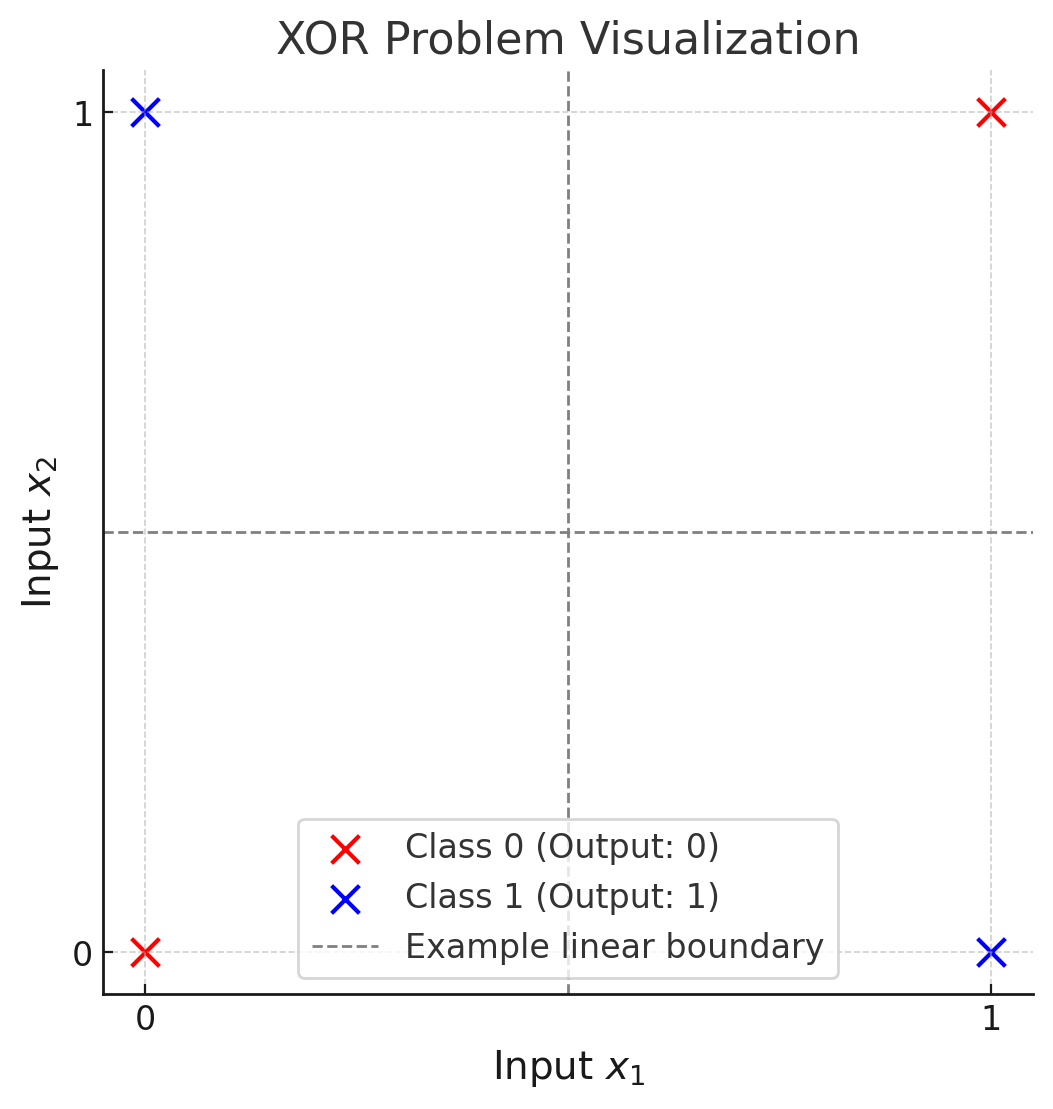
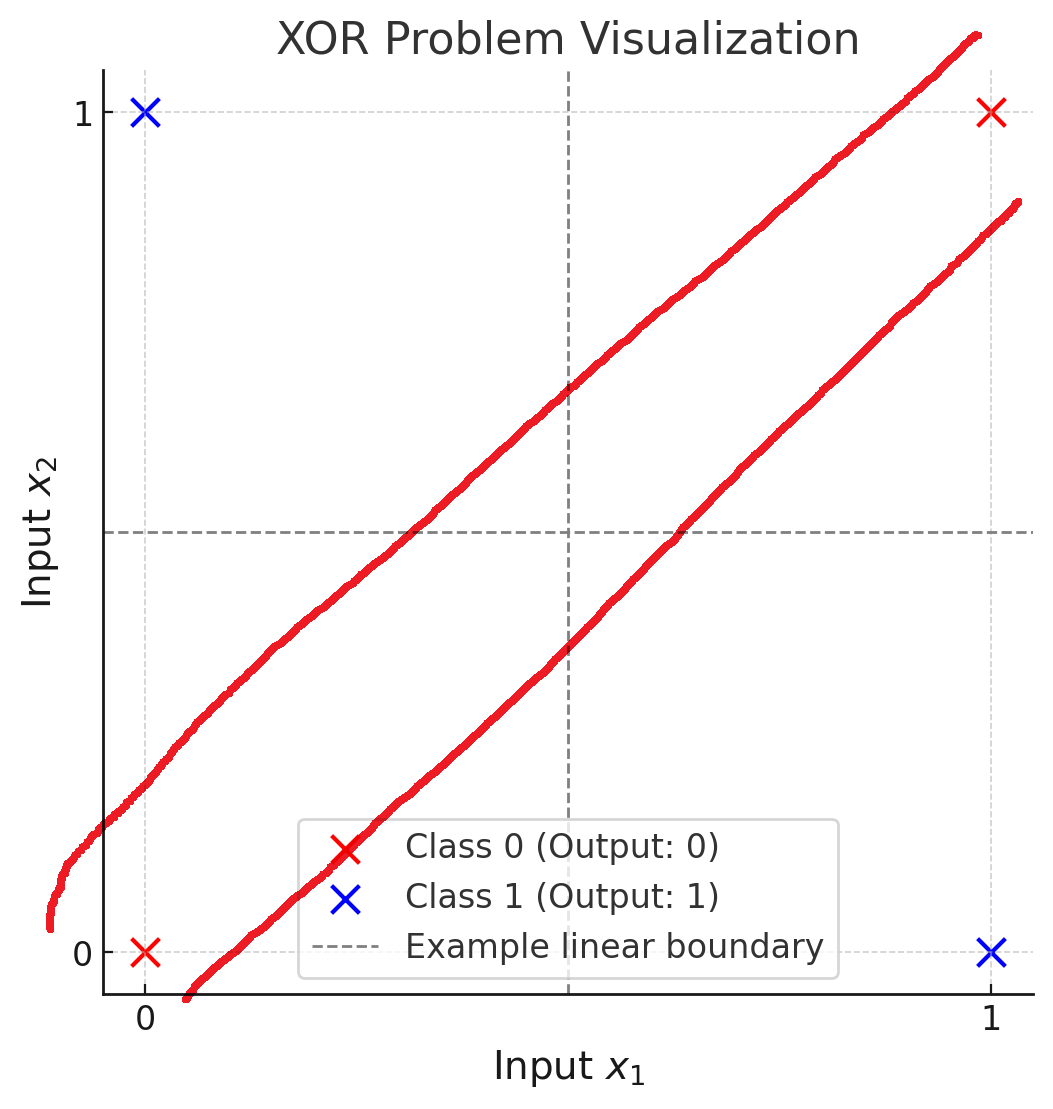
역전파 알고리즘
결국 퍼셉트론이 해결하지 못한 XOR 문제를 해결하기 위해서 역전파 알고리즘이 도입된다.
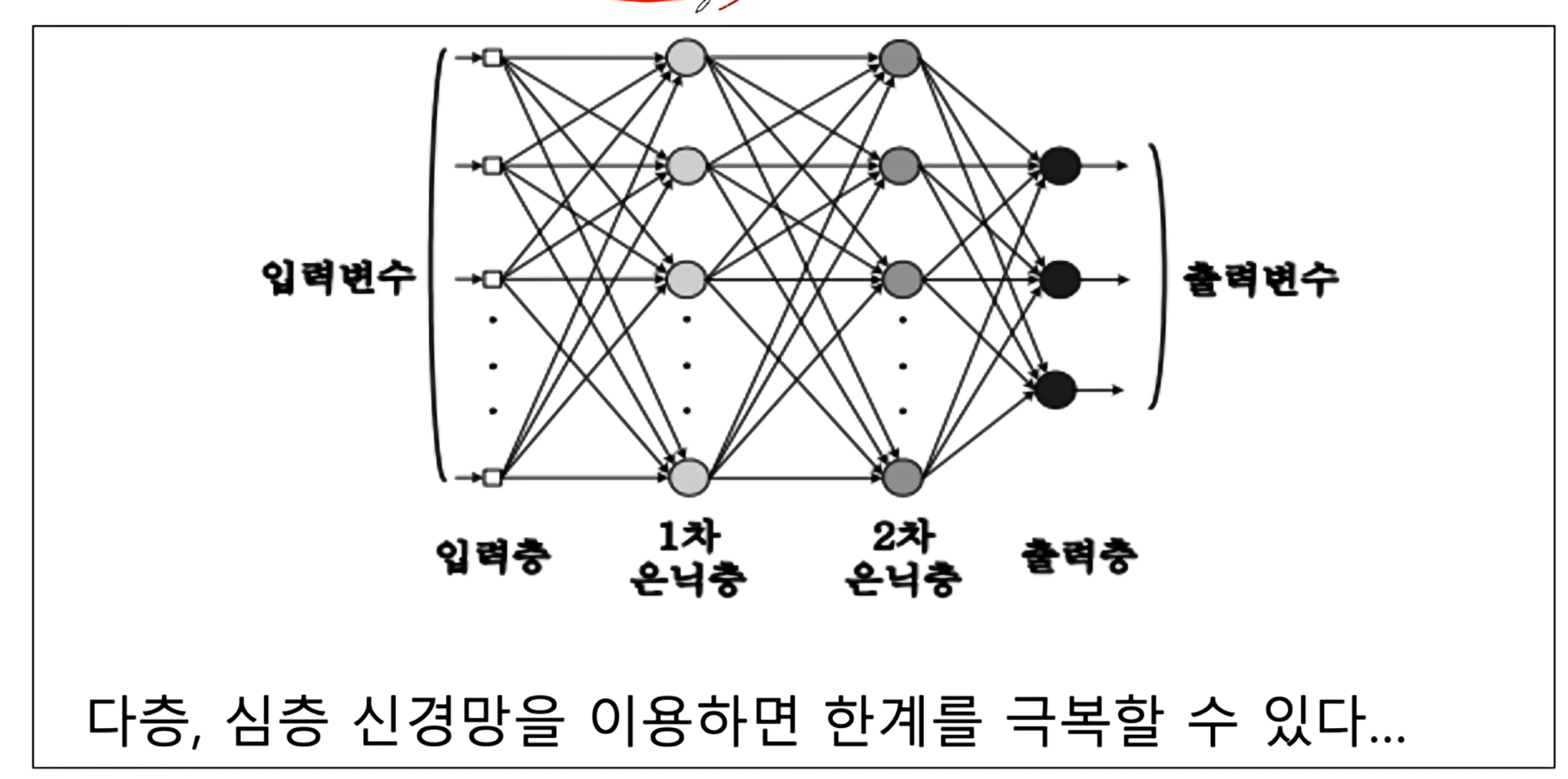
- 단층 신경망은 오차를 계산할 수 있었다.
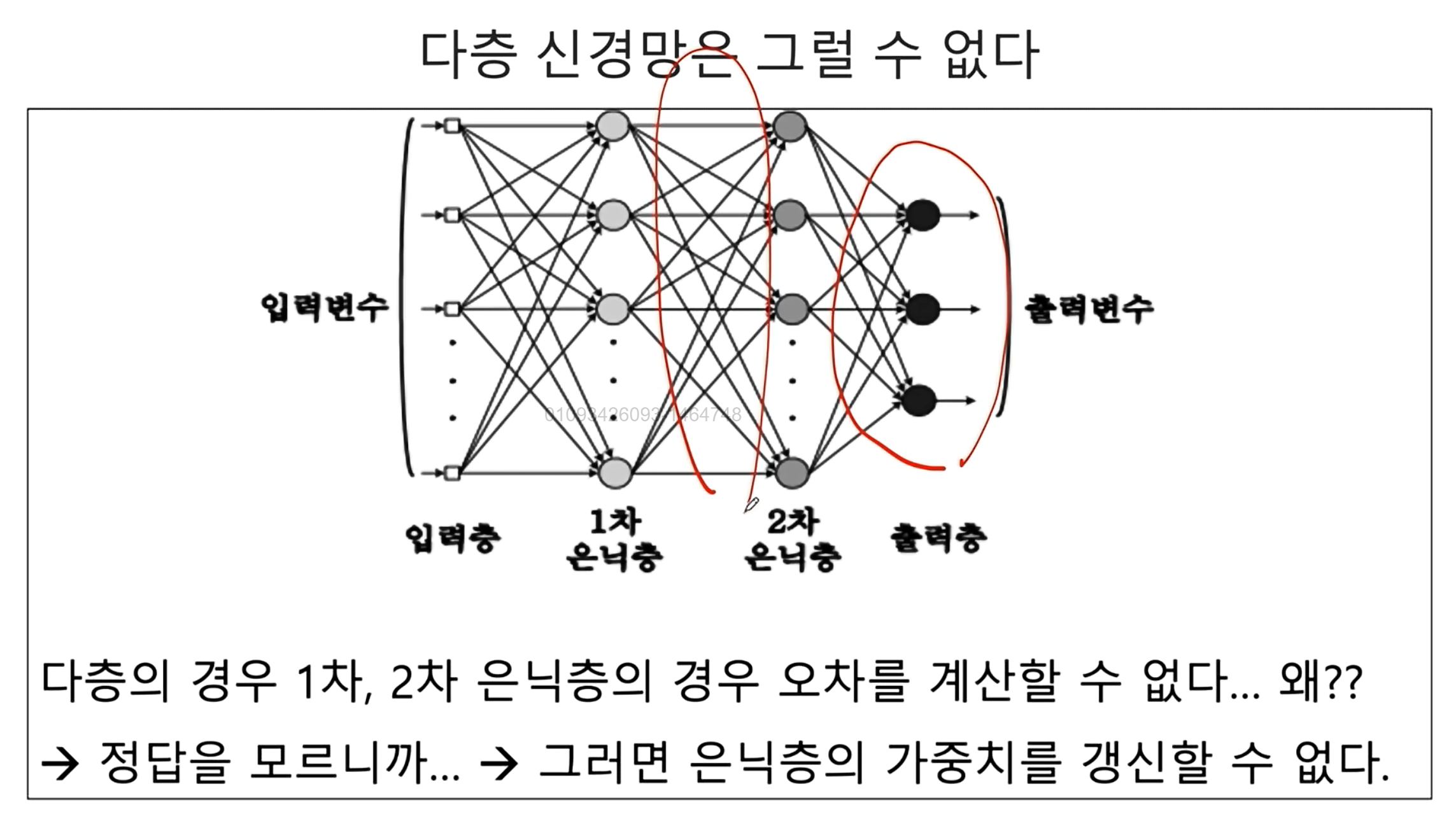
- 다층 신경망은 그럴 수 없다. 왜? → 정답을 알지 못하기 때문이다.. 출력층만 정답을 알 수 있다. 그러므로 은닉층의 가중치를 갱신할 수 없다.
결국 각 은닉층마다 뒤로 오차를 역전파(전달)함으로써 해당 문제를 해결한다.
새로운 구조
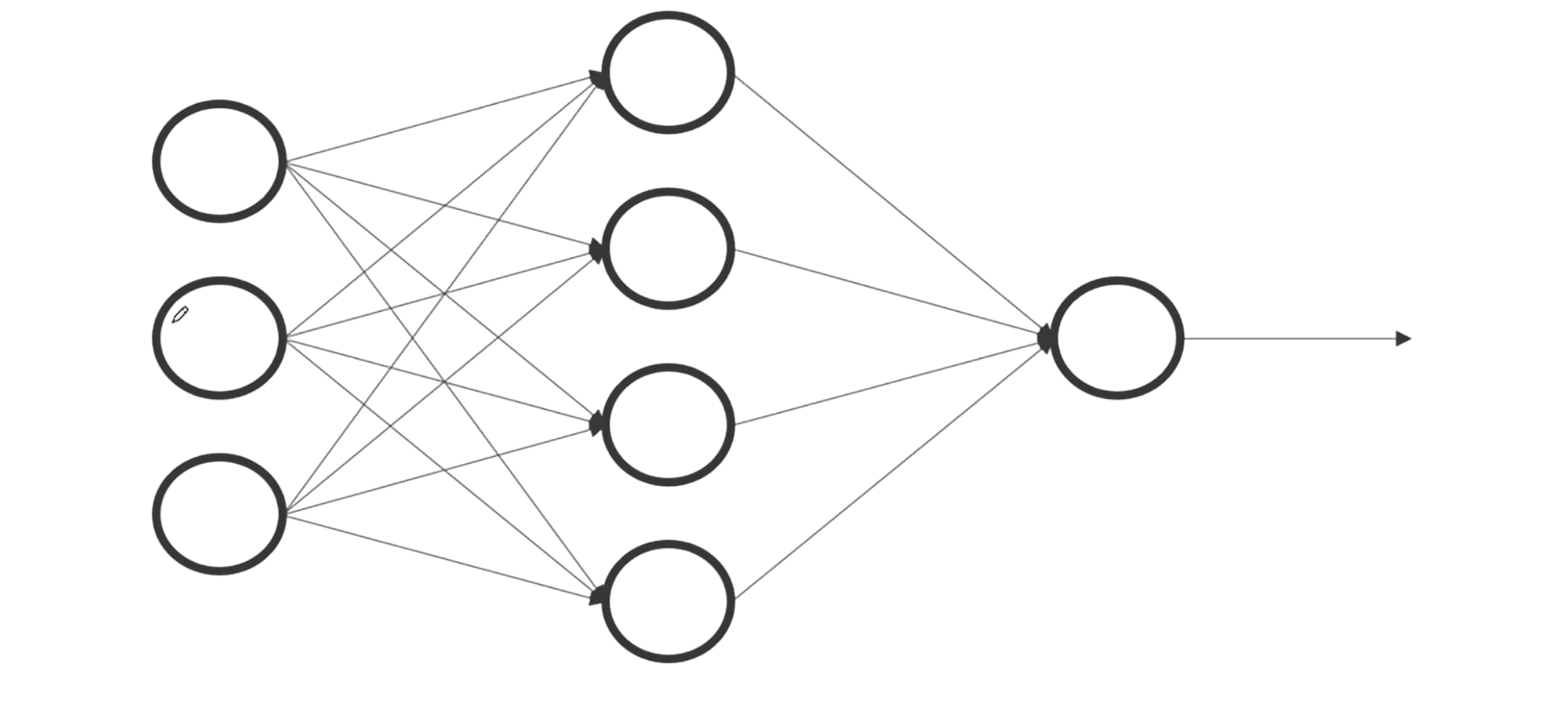
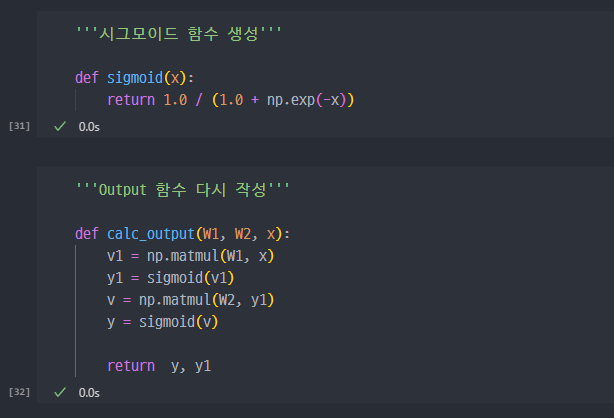
출력층에서 계산되는
delta값을 은닉층으로 전달하고 다시delta값을 은닉층에서 계산한다.
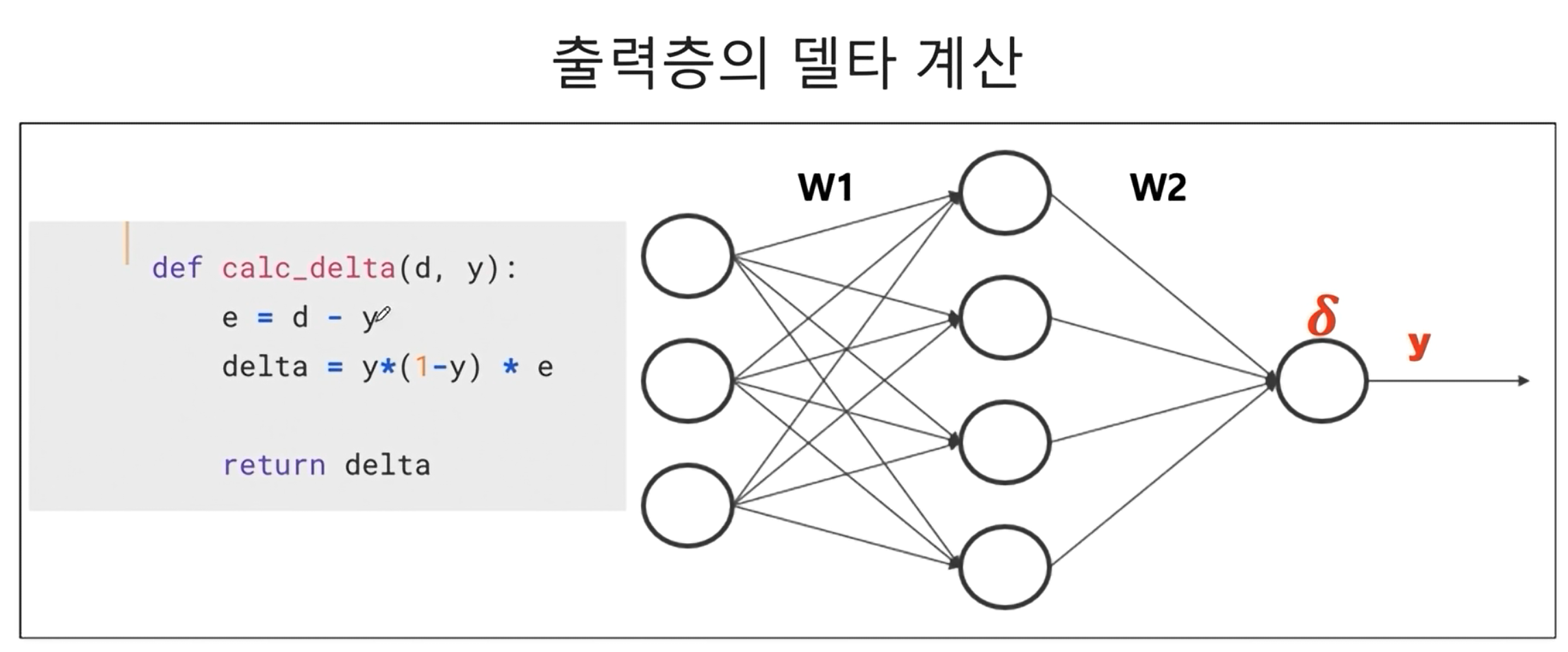
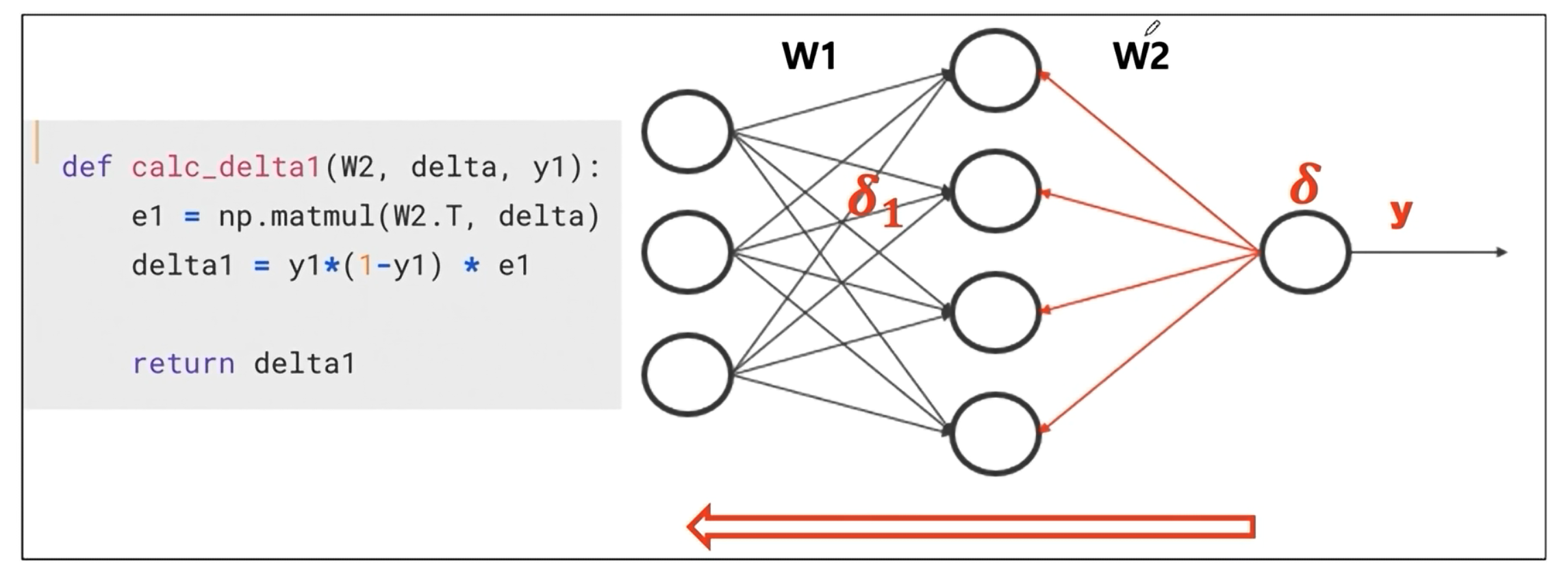
계산진행
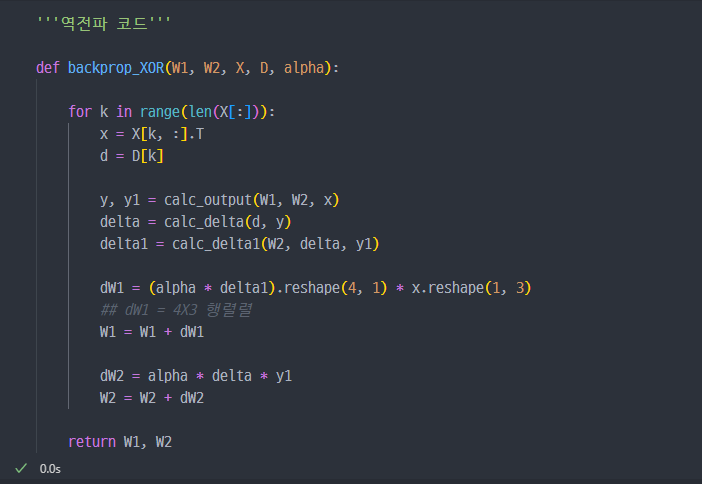
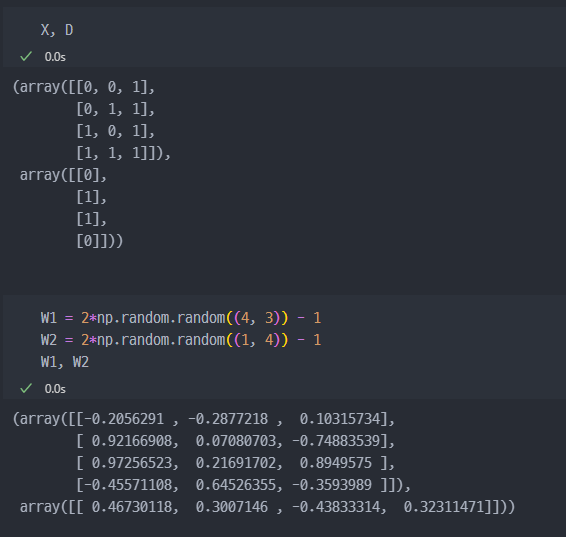
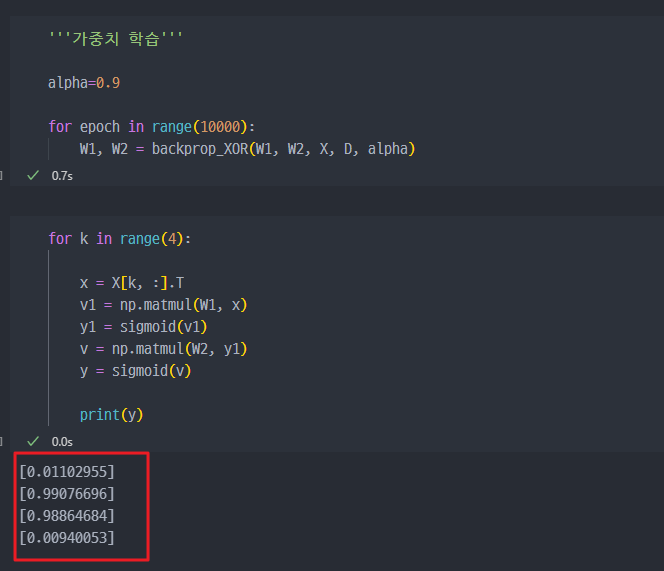
정답값은 0, 1, 1, 0 과 유사한 값이 도출되었다.
결국 첫번째 시도에서는 실패하였던 것이, 레이어를 2개 구성하고, 오차를 역전파하였더니 결과가 올바르게 도출되었다.
여기서 이해애햐 하는 것은 오차를 어떻게 뒤로 던진다는건지를 이해해야 한다. 즉 역전파.
12. 크로스엔트로피
Loss 함수 교체
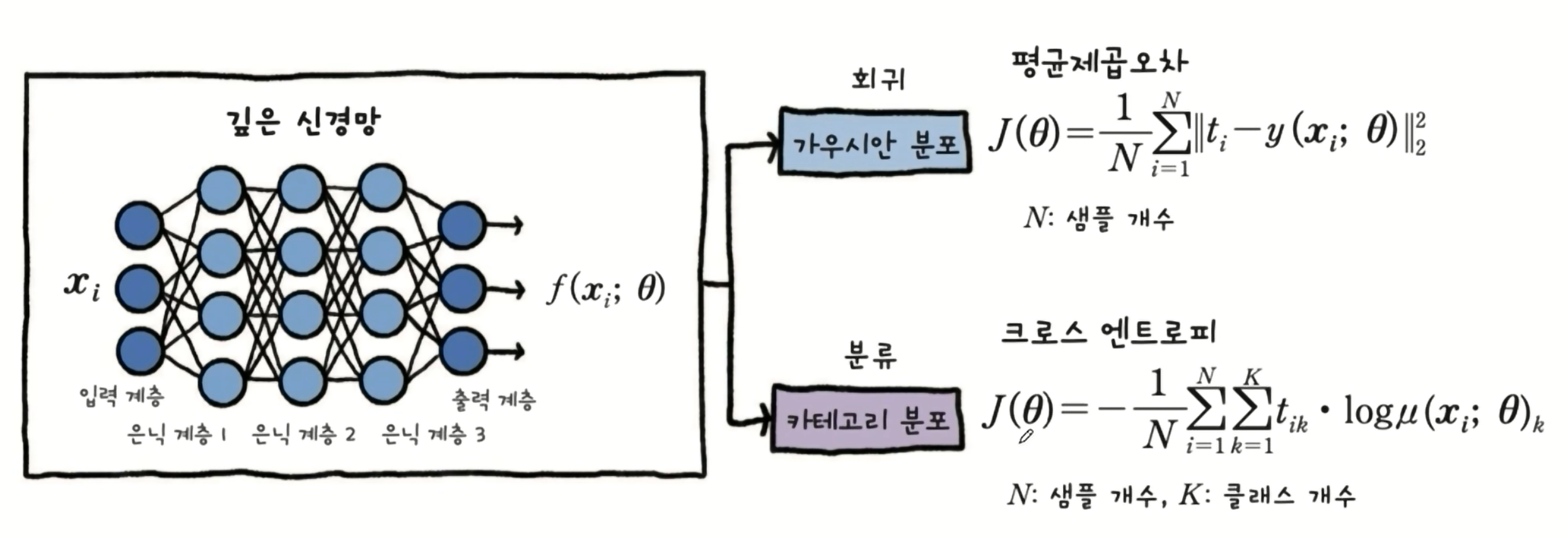
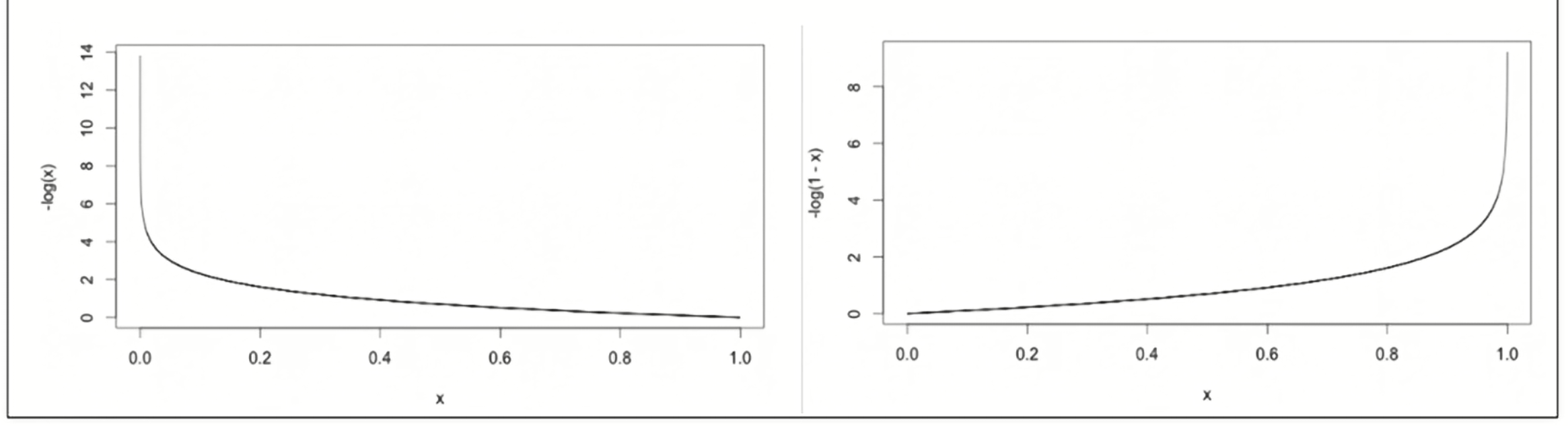
- 크로스 엔트로피 ( Cross Entropy )
크로스 엔트로피를 미분하게 되면, delta와 같다
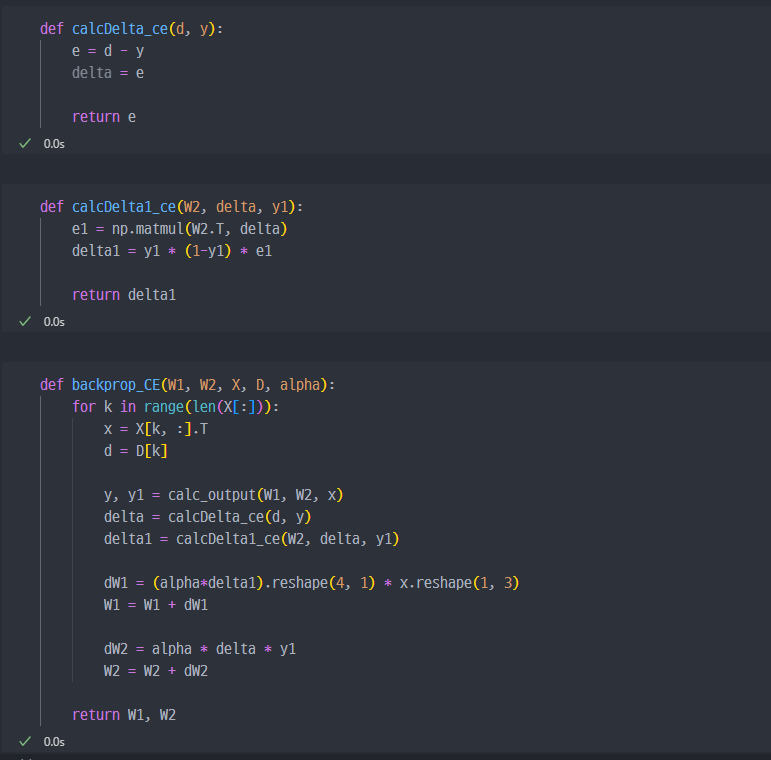
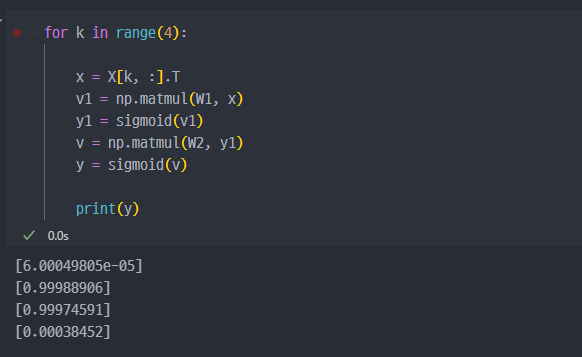
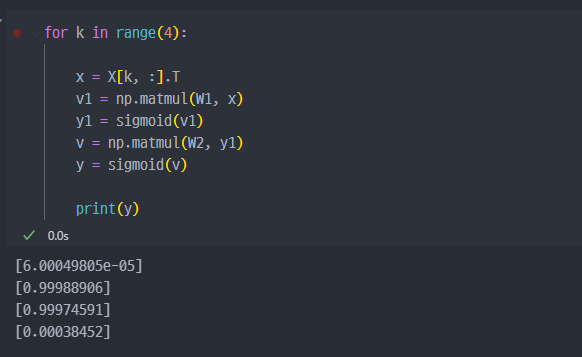
결과는 긍정적으로 나온 것을 확인할 수 있다