
Principal Component Analysis : 주성분 분석
PCA 란?
- 데이터 집합 내에 존재하는 각 데이터의 차이를 가장 날 나타내주는 요소를 찾아내는 방법. 즉 주성분 찾는 것.
- 통계 데이터 분석(주성분 찾기), 데이터 압축(차원 감소), 노이즈 제거 등 다양한 분야에서 사용
간단한 PCA 개념
-
차원축소 (Dimensionality reduction)와 변수추출(feature extraction) 기법으로 널리 쓰이고 있는 것이, 주성분 분석 -
PCA( Principal Component Analysis ) -
PCA는 데이터의 분산(Variance)을 최대한 보존하면서 서로 직교하는 새 기저(축)를 찾아, 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법 -
변수추출 (Feature Extraction)은 기존 변수를 조합해 새로운 변수를 만드는 기법.
변수선택(Feature Selection)과 다른 개념임. 구분 할 것
데이터를 어떤 벡터에 정사영시키면 차원을 낮출 수 있음. 데이터가 고유 좌표에 있을 때, 이 데이터가 가지는 좌표, 위치, 거리들의 특성을 가장 잘 보존할 수 있는 방안.
차원이 많거나 다차원은 데이터를 2차원, 1차원 등으로 축소하는 것이 PCA
PCA 란
PCA(Principal Component Analysis, 주성분 분석)는 데이터 차원을 축소하는 기법으로, 복잡한 데이터를 더 간단하게 만들기 위해 사용됩니다.
- 먼저, 데이터를 2차원 평면에 점으로 찍어보는 것을 생각해봅시다. 데이터가 여러 방향으로 퍼져있을 때,
PCA는 데이터가 가장 많이 퍼져있는 방향(즉, 변동성이 가장 큰 방향)을 찾습니다. 이 방향을 주성분(Component)이라고 합니다. - 그런 다음, 두 번째로 많이 퍼져있는 방향을 찾는데, 이 방향은 첫 번째 방향과 직교해야 합니다. 이렇게 찾은 두 개의 주성분만으로도 데이터의 중요한 정보를 많이 유지할 수 있습니다.
데이터 정규화 : 각 데이터의 평균을 0으로 맞추어 중앙을 원점으로 이동합니다.
공분산 행렬 계산 : 데이터의 공분산 행렬을 계산합니다. 이는 각 변수 간의 상관관계를 나타냅니다.
고유값과 고유벡터 계산 : 공분산 행렬의 고유값과 고유벡터를 계산합니다. 고유값은 주성분의 중요도를 나타내고, 고유벡터는 주성분의 방향을 나타냅니다.
주성분 선택 : 가장 큰 고유값을 가지는 고유벡터를 주성분으로 선택합니다. 필요한 수의 주성분을 선택하여 새로운 좌표계로 데이터를 변환합니다.
간단하게 요약하자면, PCA는 고차원 데이터를 저차원 공간으로 변환하여 데이터를 더 쉽게 분석할 수 있게 해주는 도구입니다
간단한 실습
간단한 실습을 위해, np, rand 등을 이용해서 데이터셋 생성 (행렬 형태 데이터)
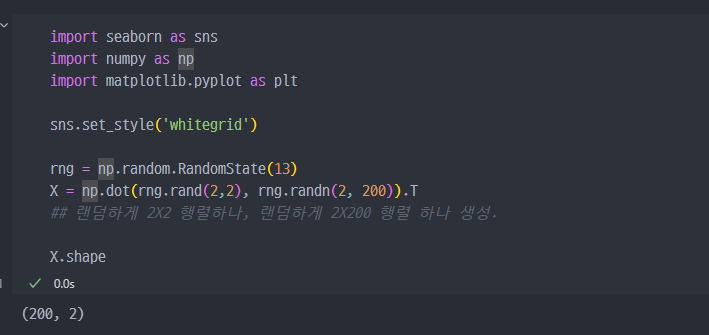
- 코드해설
-
rng=np.random.RandomState(13)- RandomState는 난수 생성을 관리하는 객체를 생성합니다.
- 13은 시드(seed)로, 난수 생성의 시작점을 고정하여 동일한 결과를 재현할 수 있도록 합니다.
- 이 객체는 이후 난수 생성에 사용됩니다.
- rng는 난수를 생성할 수 있는 객체로 저장됩니다.
-
X=np.dot(rng.rand(2, 2),rng.randn(2, 200)).Trng.rand(2, 2):[0, 1)범위에서 균일 분포로 랜덤 숫자를 생성하여 2×2 행렬을 만듭니다.[0, 1)= 0 이상이고 1 미만
rng.randn(2, 200): 평균 0, 표준편차 1인 정규분포를 따르는 난수를 생성하여 2×200 행렬을 만듭니다.np.dot(rng.rand(2, 2),rng.randn(2, 200)) : np.dot(A, B)는 두 행렬 A와 B의 행렬 곱을 수행합니다. 여기서는 2×2 행렬과 2×200 행렬의 곱이므로 결과는 2×200 행렬입니다..T: 결과 행렬을 전치(transpose)합니다. 즉, 2×200 행렬이 200×2 행렬로 바뀝니다.
위 생성된 행렬에 대해서,
matplotlib그래프로 표현
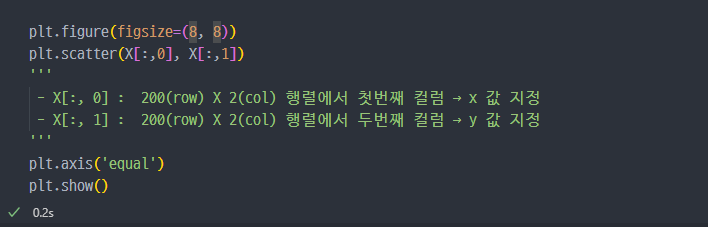
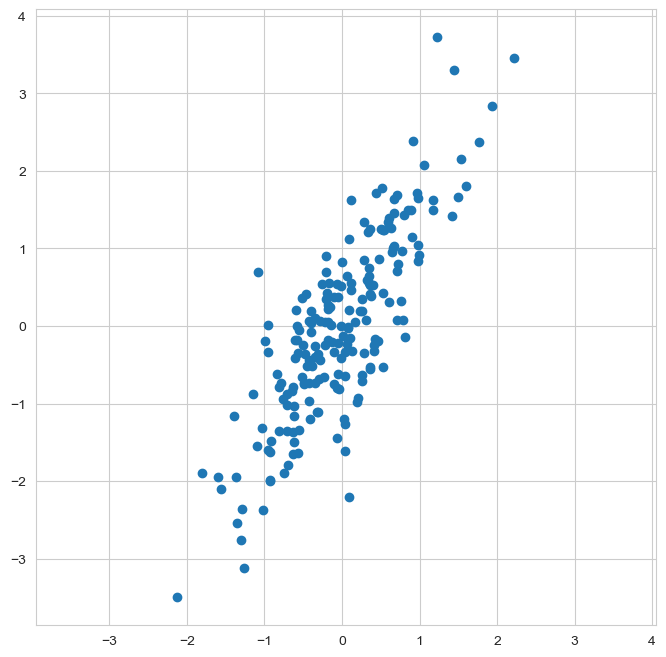
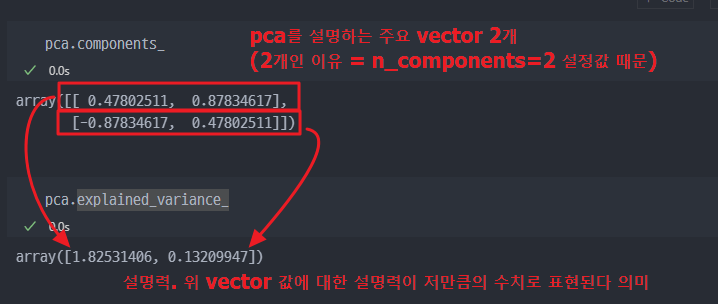
PCA진행 및fit( )진행
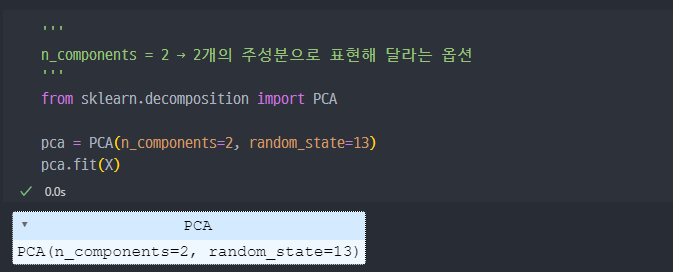
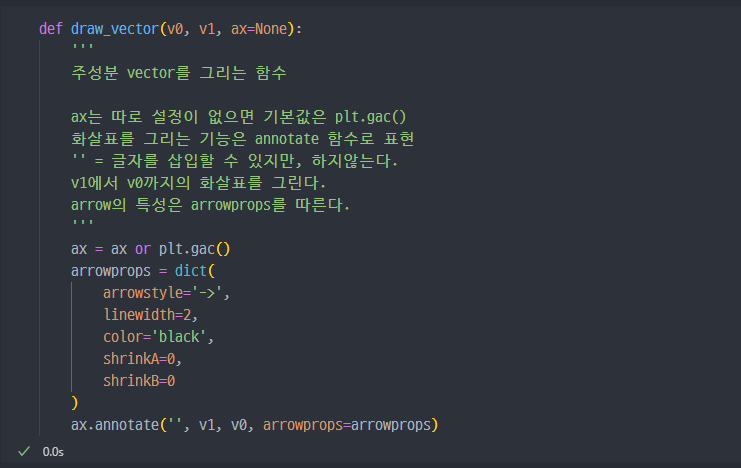
- 주성분 vector 그리는 함수 설정
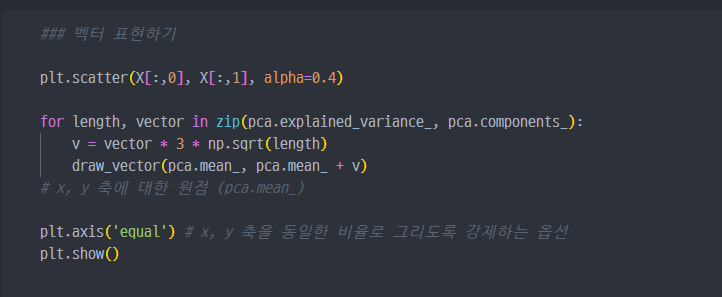
- 주성분 vector 그리기
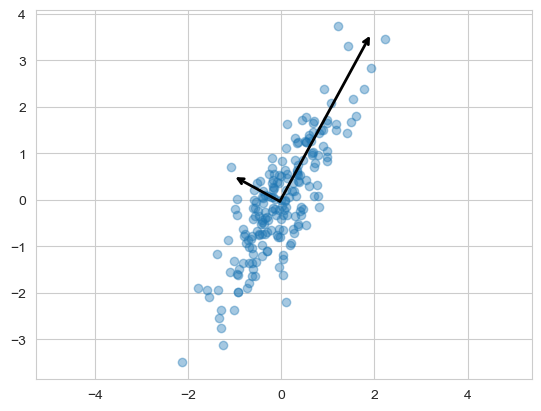
데이터의 주성분을 찾은 다음 (주성분 - 주축), 주축을 변경하는 것도 가능하다.
- n_components를 1로 변경하고 재시도
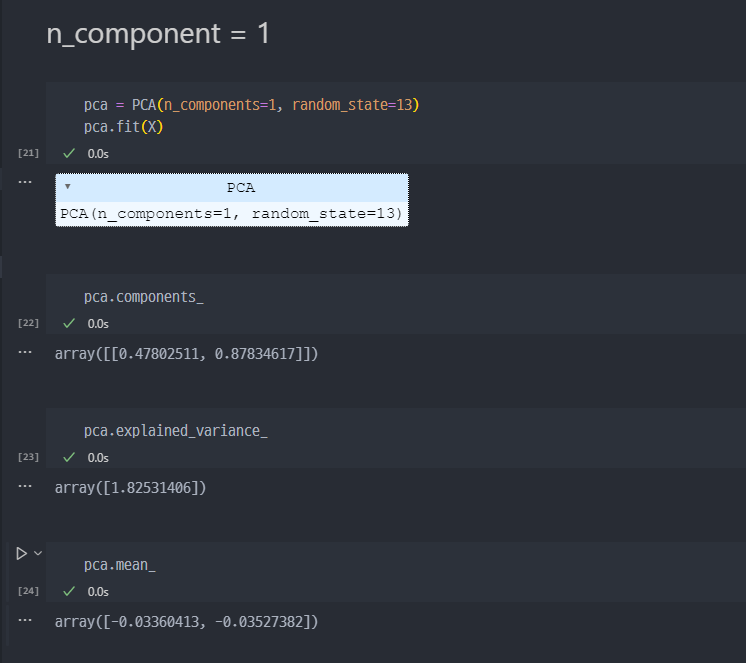
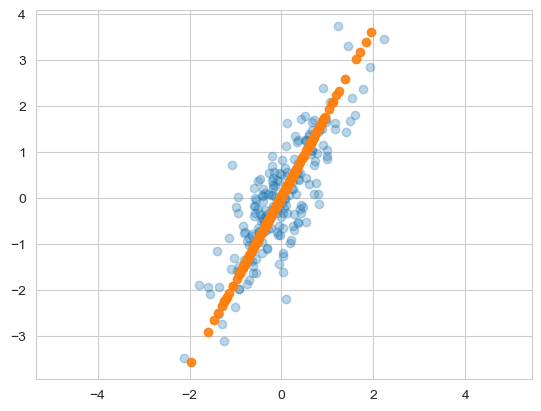
기존 X데이터와 X_new (pca에 의해서 수정된 데이터, n_components=1 옵션) 데이터를 비교하면 위 그래프와 같다. 기존 X 데이터를 pca과정을 지나, 위와 같이 직선의 형태를 띄는 데이터로 변경(수정)된 것이다.