Intuition
문제는 간단했다.
n을 1과 2로 이루어진 합으로 계산할 때 과연 몇가지 경우의수가 가능한가를 구하면 된다.
Approach 1
처음에는 규칙을 찾아보니 이런식의 규칙을 발견해서 이를 토대로 조합 함수를 만들고 다 더해보려했다.
int climbStairs(int n){
int a=n, res=0, loop=howMany(n);
for (int i=0;i<=loop;){
res+=combinations(a--,i++);
}
return res;
}
int combinations(int n, int r){
int denominator=factorial(n-r)*factorial(r);
int numerator=factorial(n);
return numerator/denominator;
}
int factorial(int k){
if (k==0){
return 1;
}
int res=1;
for (int i=k;i>1;i--){
res*=i;
}
return res;
}
int howMany(int n){
if (n==1){
return 0;
}
if (n%2==0){
return n/2;
}
else{
return (n/2)+1;
}
}그러나 이 코드는 factorial 과정에서 자료형 최대 범위를 넘어가는 것이 자명하다.
전부다 계산하지 않고 뭔가 수식을 최적화할 수 있는 방법이 있나??
Approach 2
그런데 각 n마다 최종 계산 결과를 살펴보니 피보나치 수열과같은 규칙이 보였고, 일반항도 세울 수 있었다.
그리고 이를 재귀함수로 작성했다.
int climbStairs(int n){
if (n<=3){
return n;
}
else{
return climbStairs(n-1)+climbStairs(n-2);
}
}그러나 n이 커지자 시간초과가 발생한다.
예를 들어, n=35일때 climb(34)와 climb(33)이 호출되면서 많은 겹치는 호출들이 발생한다.
원래는 여기서 DP나 Memoization을 떠올렸지만 다음 방법이 훨씬 간단해서 하지 않았다.
Approach 3 && Solution
생각을 바꿔서 앞에서부터 해보자. 2+3=5 그리고 5+x=y, x+y=z ... 이런식으로
idx는 n까지 점점커진다. pre1은 pre2는 를 의미한다.
n=4일때를 예를 들어보자. pre1과 pre2가 각각 3과 2 이므로 두 값을 더한 5가 답이된다.
n=5일때는? 앞서 n=4일때 구한 5가 지금의 pre1이 되고 n=4일때 pre1이 지금의 pre2가 되어 5+3=8이 된다.
int climbStairs(int n){
if (n<=3){
return n;
}
else{
int idx=4, pre1=3, pre2=2;
while (idx++<=n){
int tmp=pre1;
pre1=pre1+pre2;
pre2=tmp;
}
return pre1;
}
}Complexity
- Time Complexity : 하나의 while문만 보면된다.
교수님 풀이
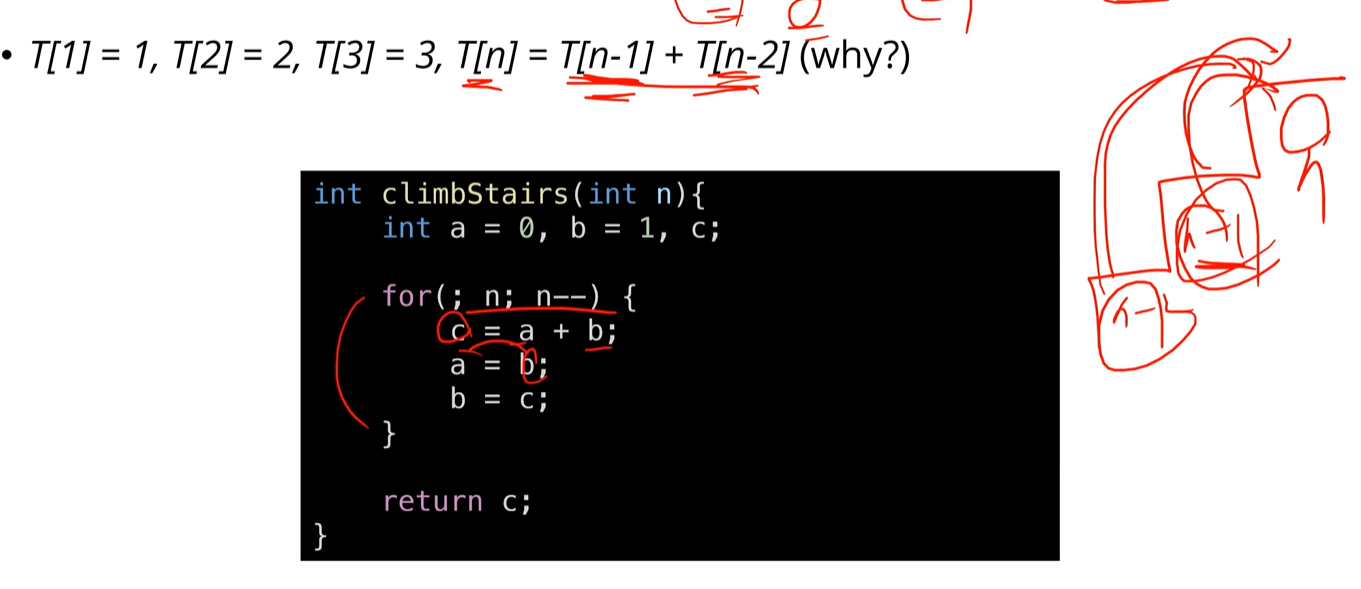
알고리즘은 동일.
중요한건 저 규칙이 왜 그런지 이해하는 것. (오른쪽 계단 그림 참고) n번째 계단을 오르려면 n-1번째 계단에서 +1하거나, n-2번째 계단에서 +2하는 경우의 수밖에 없기 때문이다!
잘못된 부분 지적 및 질문해주시면 감사하겠습니다
