[LeetCode] 172. Factorial Trailing Zeros

Intuition

팩토리얼의 계산결과 마지막에 붙는 0인 trailing zero가 몇개인지 세면된다.
기본적으로 0이 붙으면서 자릿수가 생기려면 10이 곱해져야한다.

Approach && Solution

따라서 우리는 5의 배수에 집중하면 된다. 왜냐하면 2는 5보다 충분히 많기 때문이다. 무슨소리냐면,

• $2!=2\times1$ // 2는 여기서도
• $3!=3\times2\times1$
• $4!=4\times3\times2\times1$ // 여기서도 두개나 더 $(4=2\times2)$
• $5!=5\times4\times3\times2\times1$ // 근데 5는 여기서 하나
• $6!=6\times5\times4\times3\times2\times1$ // 2는 여기서 하나 더 $(6=2\times3)$

즉, 2는 짝수마다 등장하여 그 수가 충분하기 때문에 10을 만들기 위한 조건 5와 2중 5에만 집중하면 된다는 것이다. for문도 5의 배수만 돈다.
그리고 한가지 빼먹으면 안되는 것이 5의 제곱수인 경우다. (25에는 10을 만들기 위한 재료인 5가 두개나 들어있다) 따라서 howMany5함수에서 5의 몇 제곱인지 판단해준다.

헷갈리면 안될것이 거듭제곱 이상 일때만 5가 두 개 이상이다. 가령, 25에서 5가 두개였으니 그 뒤의 5의배수인 30도 두 개로 생각한다거나 하지말자.

int trailingZeroes(int n){
    int res=0;
    for (int i=5;i<=n;i+=5){
        res+=howMany5(i);
    }
    return res;
}

int howMany5(int num){
    int res=0;
    while (num%5==0){
        res++;
        num/=5;
    }
    return res;
}

Complexity

• Time Complexity : trailing함수 안에서 howMany함수가 호출되고 둘 다 5의 배수씩 loop가 돌기 때문에 $O((logn)^2)$ 이다. 참고로 그래프로 비교해보면 아래와 같다. 제곱이긴 하지만 그래도 log는 log인가보다.
  
  howMany함수는 5로 나눠지면서 ...125, 25, 5 ,1 이니까 $log\,n$이 맞는데 trailing함수에 있는 반복문은 5씩 더해지는거니까 5, 10, 15, 20... 으로 $n/5$가 맞다. 따라서 시간복잡도는 $O(n\,log(n))$이다.

교수님 풀이

아이디어는 거의 동일한데 코드와 시간복잡도($O(log\,n)$)는 훨씬 간결하다.

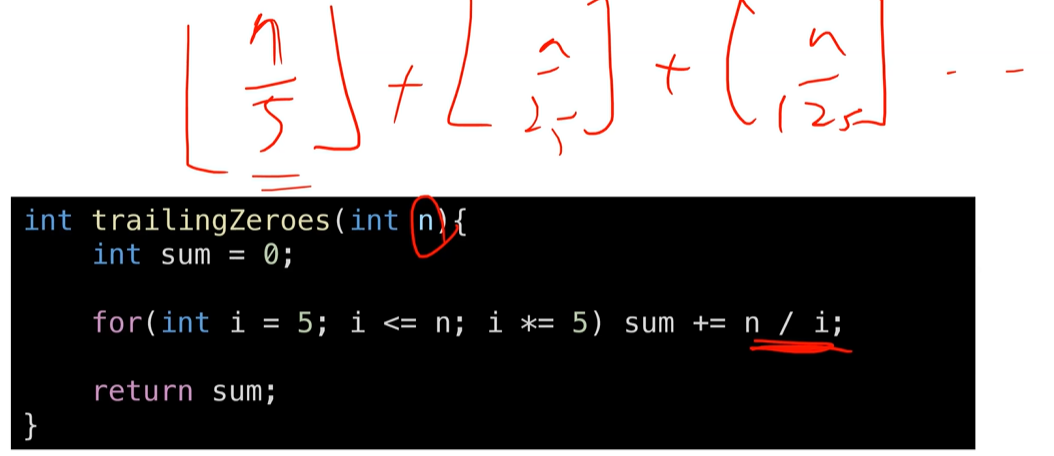
25!를 예로 들어보자. 25!중 5의 배수는 5, 10 ,15, 20, 25 이다. 다르게 표현하면 5의배수 4개와 25의 배수 1개다. 그리고 동시에 25는 5의 배수기도 하다.
1부터 13까지 중 5의 배수가 몇개냐고 물으면 어떻게 계산할까, 13/5=3.xx 임을 통해 3개라는 걸 알 수 있다. 따라서, 25!에서 trailing zeros의 개수는 $(5의\,배수의\,개수)+(25의\,배수의\,개수)$를 통해 구할 수 있다. 앞서 언급했듯이 25가 5의 배수이기도 하기 때문에 25에서 trailing zeros가 2개 나오는 것 까지 함께 계산이 되는 것이다.