Detecting the First Element in the Loop

Description

위 그림과 같이 Single Linked List에서 한 개 이하의 loop가 존재한다고 가정했을 때, 그 loop가 시작하는 위치를 찾는 문제이다. 단, loop의 마지막은 마지막 index이다.

Naïve Approach

• 연결 리스트 일순 과정에서 각각의 node의 address를 배열에 담아놓는다. loop가 존재한다면 같은 address를 한 번 더 방문할 것이고 이때 배열에 해당 address가 존재한다면 그것이 정답 node가 된다.

  결국 node개수만큼 memory를 copy하는 것과 같은 효과이기 때문에 inefficent하다.

• 구조체에 visited 멤버변수를 추가하여 확인한다.

  일반적인 경우 구조체를 변경한다는 것은 불가능하다.

Floyd's Tortoise and Hare Algorithm

직역하면 플로이드의 거북이와 토끼 알고리즘인데, 이름답게 속도가 다른 두 개의 포인터를 사용한다.

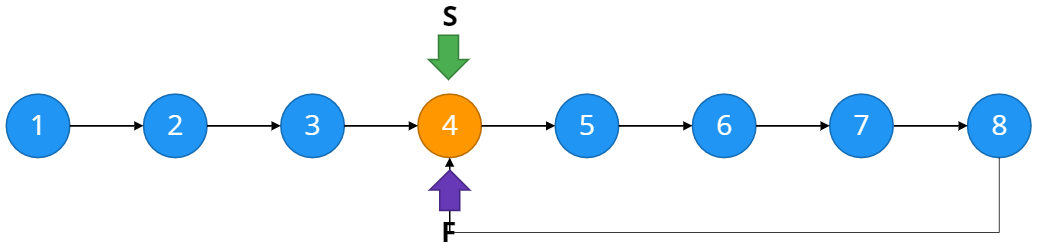
• Slow pointer (S, tortoise) : moves by 1 node at a time
• Fast pointer (F, hare) : moves by 2 nodes at a time
  

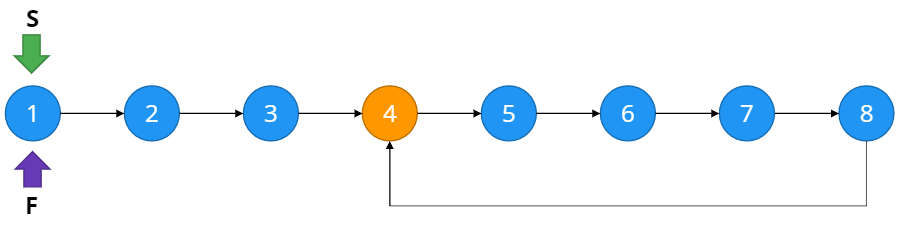
Phase 1

두 포인터가 첫번째 인덱스에서 출발하여 다시 만날때까지 계속한다.
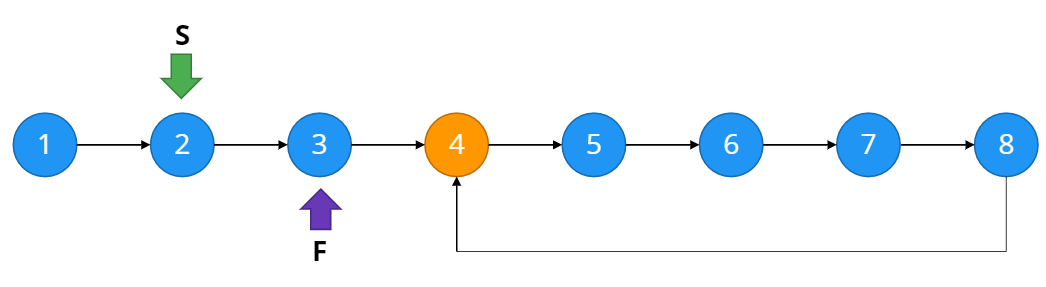
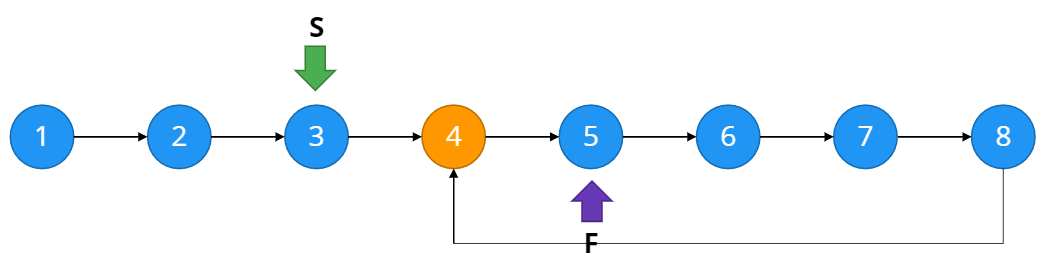
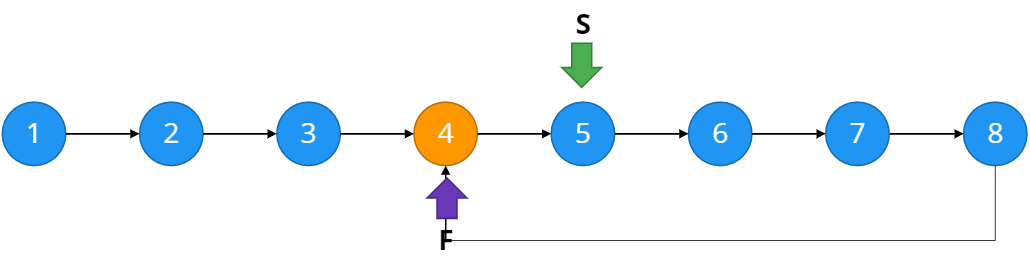
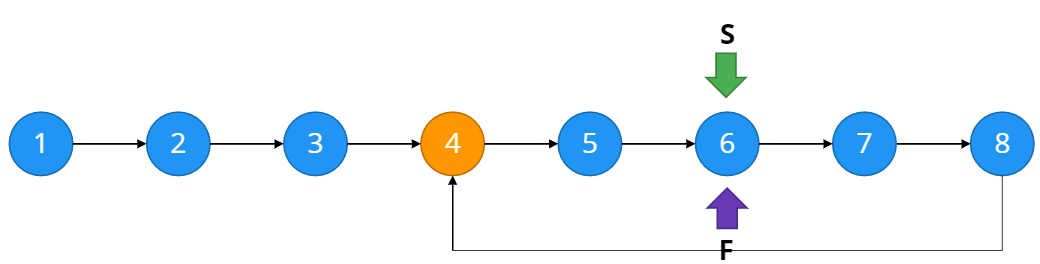위와 같이 두 포인터가 다시 만났다면 loop가 존재한다는 것이다. (만약 존재하지 않는다면 두 포인터는 만나지 않는다)

Phase 2

그러나 우리가 찾고자 하는 것은 이 loop의 시작점이다. 이를 찾기 위해, 두 포인터 중 하나를 첫번째 인덱스로 옮기고 두 포인터 모두 한 node씩 이동시킨다. 두 포인터가 다시 한 번 만나는 지점이 loop의 시작점이다.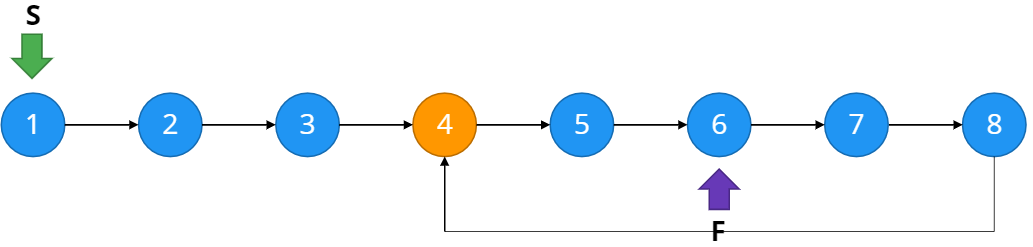

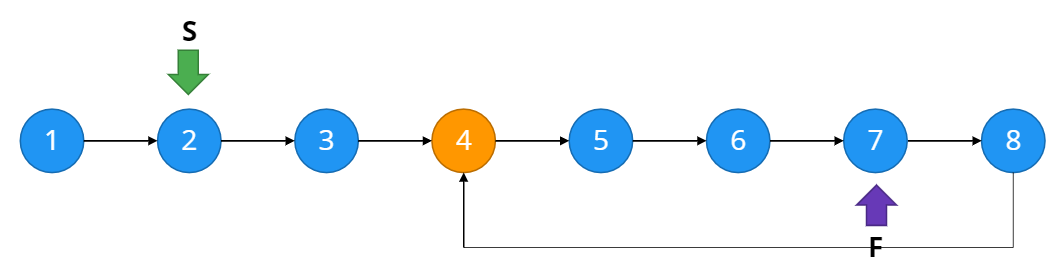
Proof

첫번째 인덱스부터 loop의 첫 element까지의 거리를 $M$, loop의 첫 element부터 두 포인터가 최초로 만난 지점까지의 거리를 $K$, loop의 길이를 $L$이라 하자.
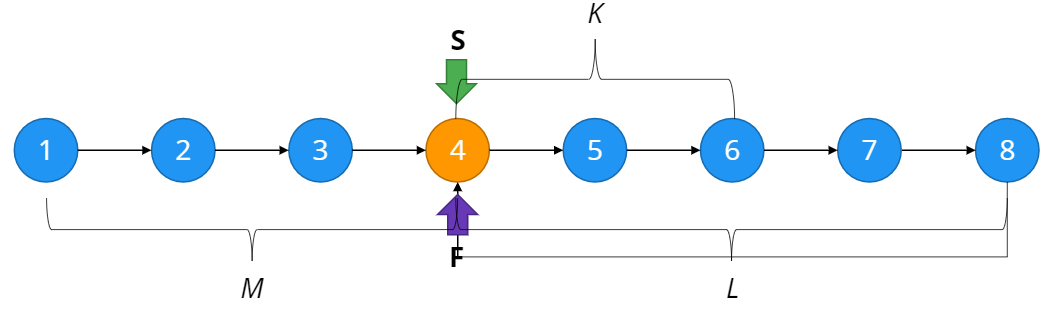Phase2에서 S포인터가 M만큼 이동하는 동안, F포인터가 $x$바퀴 순회하므로 아래와 같은 식을 세울 수 있다.

$M=Lx -K$ (단, $x$는 임의의 상수)   $\cdots$ ①

Phase1에서 포인터 S와 F가 loop를 각각 $y,z$ 바퀴 순회했다고 하면 이동한 거리는
$M+Ly+K,$ $M+Lz+k$ (단, $y,z$는 임의의 상수)로 표현할 수 있다.

이때, F의 속력은 S의 2배이므로 이동한 거리 2배가 된다.

$2(M+Ly+K)=M+Lz+k$
$M=L(z-2y)-K$  $\cdots$ ②

①, ②를 통해 알고리즘이 성립함을 보일 수 있다.


이 알고리즘을 사용하게 되면 시간복잡도가 $O(N)$이 되기 때문에 Competition보다는, 주로 Interview에서 등장한다고 한다.

Bonus Problem

이 문제에서 이어지는 문제다.

linked list에서 node를 지울 때, target node의 직전 node에 포인터를 두고 target을 지우기 마련인데, 만약 target node로 이미 포인터를 옮겼을 때는 어떻게 해야하는가에 대한 문제이다. 단, 항상 target node의 다음 node는 존재한다.

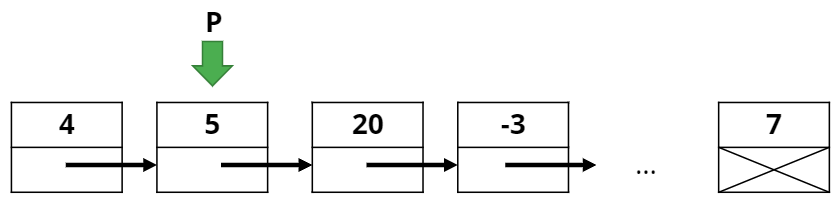
아래 그림을 예시로 들자면, 5를 지워야하는 상황인데 이미 포인터가 5에 있는 상황이다.

방법은 간단하다. target node의 next node member를 현재 target node에 copy하고 next node를 지우는 것이다.

이러한 해결 방법은 주어진 예시의 memeber가 정수인것과 같이 copy가 간단한 경우에만 성립한다. memeber에 file이 존재하는 등의 경우에는 copy가 쉽지 않기 때문이다.

지적 및 질문 환영