Intuition
값이 올라가기 시작하는 지점부터 내려오는 지점까지의 길이의 최댓값을 구하는 문제이다. Literally 산을 찾으면 된다. 그러기 위해선 올라가는 부분과 내려가는 부분, 그리고 하산이 끝나는 지점을 특정시켜줄 수 있어야 한다.
Approach
올라가는 부분과 내려가는 부분의 길이를 count한 다음 하산이 끝난시점에서 max값을 결정시켜주는 일련의 작업을 반복하는 흐름으로 진행된다.
등산부분의 길이, 하산부분의 길이, 최댓값을 담을 변수를 선언 및 초기화한다.
int up,down,max;
up=down=max=0;array의 연속된 두 원소()의 값을 비교할 것이므로 (배열의 크기)-1만큼 순회한다.
for (int i=0;i<arrSize-1;i++){
...
}
- 등산 및 하산 완료 파트
산이 끝나는 지점을 특정시키고 지금까지 count된 up과 down의 길이를 통해 max값을 결정시키는 부분이다.
산이 끝나는 지점은 우선, 다음 원소와 비교했을 때 그 값이 더 작아지지만 않으면 된다. 더 큰 값이 나오든, 같은 값이 나오든 상관없다는 뜻이다.
그리고 앞서 등산하는 파트와 하산하는 파트가 있었기 때문에 up, down 변수가 0보다 큰 상태이다.
그러나 이 부분은 산이 끝나는 지점이자 동시에 새로운 산이 시작하는 지점이 될 수도 있기 때문에
다음 원소와 비교했을 때 그 값이 더 크다면 up 변수를 업데이트 해줘야한다. (ex. 1 5 1 3)
if (!(arr[i]>arr[i+1])&&down){ // up 변수 미체크 사유는 후술
if (max<up+down+1) max=up+down+1;
up=down=0;
if (arr[i]<arr[i+1]) up++; // 산이 끝나는 지점이자 동시에 시작하는 지점
}
- 하산 파트
기본적으로 다음 원소가 더 작아야한다. 또한, 이전에 등산 파트가 존재했어야 한다. 즉, up 변수가 0보다 커야한다.
그리고 이렇듯 up 변수가 0보다 클때만 down 변수가 업데이트 되므로, 등산 및 하산 완료 파트를 체크할때 down 변수만 체크해주면 된다.- 등산 파트
다음 원소가 더 크다면 up변수를 업데이트 해주면 된다.- 그 외
1 3 5 5 와 같이 등산하다가 같은 숫자가 나온다든지, 산과 관련 없는 부분들도 존재하므로 따로 처리해줘야한다.
for (int i=0;i<arrSize-1;i++){
if (!(arr[i]>arr[i+1])&&down){ // 등산 및 하산 완료 파트
if (max<up+down+1) max=up+down+1;
up=down=0;
if (arr[i]<arr[i+1]) up++;
}
else if (arr[i]>arr[i+1]&&up) down++; // 하산파트
else if (arr[i]<arr[i+1]) up++; // 등산파트
else up=down=0; // 그 외
}그런데, 위 반복문이 (배열의 크기)-1만큼 순회하므로 1 5 1 과 같이 마지막 원소에서 산이 끝나게 되는 경우는 체크를 해줄 수가 없다.
따라서 마지막에, up down 변수를 체크해 최종적으로 max값을 결정지어준다.
if (up>0&&down>0){
if (max<up+down+1) max=up+down+1;
}Solution
int longestMountain(int* arr, int arrSize){
int up,down,max;
up=down=max=0;
for (int i=0;i<arrSize-1;i++){
if (!(arr[i]>arr[i+1])&&down){
if (max<up+down+1) max=up+down+1;
up=down=0;
if (arr[i]<arr[i+1]) up++;
}
else if (arr[i]>arr[i+1]&&up) down++;
else if (arr[i]<arr[i+1]) up++;
else up=down=0;
}
if (up>0&&down>0){
if (max<up+down+1) max=up+down+1;
}
return max;
}Complexity
Time Complexity && Space Complexity
교수님 풀이
two pointers를 이용한 풀이는 전반적 로직이 동일하고 교수님께서도 그리 좋은 풀이는 아니라고 언급하신 관계로 넘어가도록 한다.
이 풀이는 올라가는 부분의 길이와 내려가는 부분의 길이를 각각 세고 두 부분의 길이의 합이 가장 큰 곳을 찾는 방식으로 진행된다.
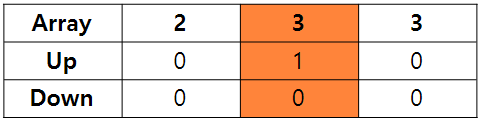
up배열부터 살펴보겠다.
우선 최초 인덱스 up[0]은 0으로 시작한다.
4에서 2로 넘어갈 때에는 그 값이 증가하지 않으므로 그대로 0을 할당시켜준다.
2에서 3으로 넘어갈 때에는 값이 증가하므로 이전 인덱스보다 +1시킨 값을 할당시켜준다.
3에서 5도 마찬가지이다.
하지만 5에서 1은 다시 감소하므로 0을 다시 할당시켜준다.
down배열은 뒤에서부터 거꾸로 순회하면 된다.
int *up=(int*)malloc(sizeof(int)*arrSize);
int *down=(int*)malloc(sizeof(int)*arrSize);
up[0]=0,down[arrSize-1]=0;
int upCnt, downCnt;
upCnt=downCnt=0;
for (int i=1;i<arrSize;i++){
if (arr[i-1]<arr[i]) upCnt++;
else upCnt=0;
up[i]=upCnt;
if (arr[arrSize-i]<arr[arrSize-i-1]) downCnt++;
else downCnt=0;
down[arrSize-i-1]=downCnt;
}이제 배열을 순회하며 그 합이 가장 큰 곳을 찾으면 된다.
이때 주의할 점은 배열의 값이 0인 부분 즉, 아래 예시에서는 올라가는 파트는 맞으나 내려가는 파트는 아닌부분과 같이 산 모양 여부를 판단하기 위한 작업을 진행해주어야한다.
이를 위해선 up down 배열의 값이 0보다 큰지 확인해주면 된다.
int max=0;
for (int i=0;i<arrSize;i++){
if (up[i]&&down[i]&&(up[i]+down[i]+1>max)) max=up[i]+down[i]+1;
}Solution
int longestMountain(int* arr, int arrSize){
int *up=(int*)malloc(sizeof(int)*arrSize);
int *down=(int*)malloc(sizeof(int)*arrSize);
up[0]=0,down[arrSize-1]=0;
int upCnt, downCnt;
upCnt=downCnt=0;
for (int i=1;i<arrSize;i++){
if (arr[i-1]<arr[i]) upCnt++;
else upCnt=0;
up[i]=upCnt;
if (arr[arrSize-i]<arr[arrSize-i-1]) downCnt++;
else downCnt=0;
down[arrSize-i-1]=downCnt;
}
int max=0;
for (int i=0;i<arrSize;i++){
if (up[i]&&down[i]&&(up[i]+down[i]+1>max)) max=up[i]+down[i]+1;
}
free(up), free(down);
return max;
}Complexity
Time Complexity && Space Complexity