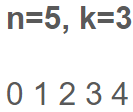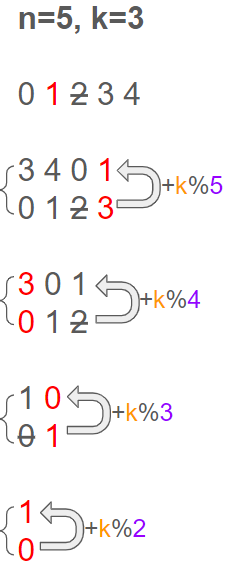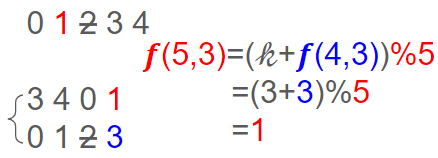[LeetCode] 1823. Find the Winner of the Circular Game

Ho__sing·2023년 12월 29일

C leetcode linkedlist loop recursion

문제해결 자체 재수강

목록 보기

23/48

Intuition

문제의 구조 자체가 Circular Linked List와 매우 유사하다. Node를 하나씩 순회하며 처음과 끝이 연결된 구조이고, Node를 삭제할 수 있다.

Approach & Solution

#include <stdlib.h>

typedef struct linkedlist_{
    int val;
    struct linkedlist_* next;
}linkedlist;

linkedlist* new_node(int val){
    linkedlist* new_node=(linkedlist*)malloc(sizeof(linkedlist));
    new_node->val=val;
    new_node->next=NULL;
    return new_node;
}

void del (linkedlist* targetM1){
    linkedlist* temp=targetM1->next->next;
    free(targetM1->next);
    targetM1->next=temp;
}

int findTheWinner(int n, int k) {
    if (k==1) return n;
    int printerN=n;
    linkedlist* head=new_node(1);
    linkedlist* cur=head;
    for (int i=1;i<n;i++){
        cur->next=new_node(i+1);
        cur=cur->next;
    }
    cur->next=head;

    cur=head;
    while (--n){
        for (int i=0;i<k-2;i++){
            cur=cur->next;
        }
        del(cur);
        cur=cur->next;
    }
    
    return cur->val;
}

Complexity

Time Complexity

매 턴마다 K번씩 순회를 하는 과정을 N개만큼 반복한다. $O(KN)$

Space Complexity

Node 개수만큼의 공간이 필요하다. $O(N)$

교수님 풀이

n=5, k=2이라고 하자.
1 2 3 4 5 에서 1 2 3 4 5 가 되고 다음턴에는
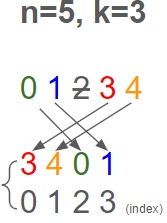
1 3 4 5가 된다. 이때 3부터 출발하므로 3 4 5 1로 생각한다면 더 간편할 것이다.

그리고 결국 중요한 것은 3 4 5 1 자체의 숫자가 아니라 위치 즉, 인덱스이다. 3 이라는 숫자보다 그것이 현재 0번째라는 것, 그리고 그 다음 사라지는 숫자는 k-1만큼 더 순회한 곳에 위치한다는 것이 중요하다.

인덱스로 생각하면 매 원소를 순회할 필요없이 k-1만큼 더해준 결과값의 원소를 지워주면 된다. 이때, 마지막 인덱스를 넘어가면 다시 처음 인덱스로 돌아오므로 (k-1)%n의 원소가 지워진다고 표현할 수 있다.

나머지 또한 0부터 나눈 숫자전까지의 범위로 결과가 나온다는 점과 우리가 인덱스를 활용한다는 점을 종합해 봤을 때, 주어진 Input을 인덱스처럼 0부터 처리하는 것이 더 낫다고 생각해 볼 수 있다.

아래와 같은 상황이 있다고 가정 했을 때, 본격적으로 원소를 지워보겠다.

남은 숫자는 다음 숫자인 3부터 순서만 바꿔서 다시 써볼 수 있고, 이를 다시 인덱스로도 표현해볼 수 있다.

그 다음 과정에서 0123은 인덱스가 아니라 처음의 01234과 같은 역할을 다시 하게 된다.

이 같은 과정이 반복되면 결국 마지막 결과는 아래와 같다.여기서 중요한 것은 마지막 남은 0이 가장 처음 01234 중 어느 것으로 부터 왔느냐는 것이다.

역추적의 결과이다.그리고 원래 list는 1부터 시작하므로 정답은 2가 된다.

이제 해야 할 일은 이 일련의 과정을 코드로 작성 즉, 수식화 시키는 것이다.

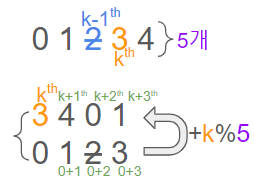
역추적 과정을 다시 한 번 살펴보겠다. 우선 여기서 2는 인덱스 k-1의 원소이고 그에 따라 다음 시작 원소는 인덱스 k에 위치한다.따라서 셋째줄의 0123에서 둘째줄의 3401을 얻기 위해서는 +k를 해줘야함을 알 수 있다. 그러나, 원래 첫째줄의 01234에서 알 수 있듯이 k+2번째 인덱스는 존재하지 않는다. 따라서 나머지 연산을 통해 원래 값을 구해줘야 한다.

이를 통해 우리는 셋째줄의 3이 곧 둘째줄의 1을 나타냄을 알 수 있고 이 1은 첫째줄과 숫서만 바꾼 것이므로 셋째줄의 3이 첫째줄의 1임을 알 수 있다. 그리고 이 과정을 1개가 남았던 시점부터 원래 배열로 돌아올 때 까지의 과정에 적용시킬 수 있다.

인덱스이므로 마지막 남는 원소는 항상 0, bottom to top의 각 시퀀스마다 보이는 규칙성, 이 두 가지를 종합해보았을 때 우리는 재귀함수(또는 loop)를 고려해 볼 수 있다. 전자의 경우 base condition, 후자는 점화식이 될 것이다.

각 시퀀스 마다 남아있는 원소의 개수를 m이라 할 때, 아래와 같은 점화식을 세울 수 있다.

$f(m,k)=\{k+f(m-1,k)\}\%n$

Solution

int func(int n, int k){
    if (n==1) return 0;
    return (k+func(n-1,k))%n;
}

int findTheWinner(int n, int k) {
    return func(n,k)+1; // index로 취급하였으므로 다시 1을 추가해줘야한다.
}