Intuition
contiguous한 subarray를 찾아야 하는 점에서 two pointer의 느낌을 받을 수 있었다.
subarray의 양 끝을 조절하며 k와 곱을 비교해가면 문제를 풀 수 있을 것이라 생각했다.
Approach
subarray의 양 끝을 two pointer로 잡아준다. 초기 시작은 l과 r 모두 0이다.
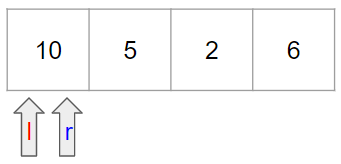 k보다 곱이 작으므로 subarray의 길이만큼을 output에 더해준다. r도 +1해준다.
k보다 곱이 작으므로 subarray의 길이만큼을 output에 더해준다. r도 +1해준다.
이때, subarray의 길이만큼 output에 더하는 이유를 설명해보겠다.
가령 [a,b] 배열이 있다면 여기서 만들 수 있는 subarray의 개수는 [a],[b],[a,b] 이렇게 3개이다. 그런데 여기에 c가 더해져 [a,b,c]가 되면 기존의 subarray에 더불어 [a,b,c],[b,c],[c] 3개가 추가되어 총 6개가 된다.
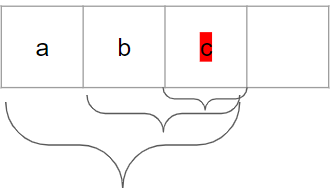
즉, 길이가 n인 array에서 만들 수 있는 contiguous subarray는 직전 n-1 array에서 만들수 있었던 subarray의 개수+n 이라는 뜻이다.
다시 돌아와서,
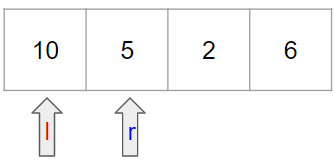 마찬가지 이유로 output을 2만큼 더해주고 r을 옮겨준다.
마찬가지 이유로 output을 2만큼 더해주고 r을 옮겨준다.
그러나 다음 case에는 문제가 발생한다. 곱이 k와 같기 때문이다.
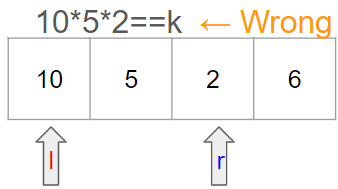
이 경우에는 l을 한칸 옮겨주고 일련의 과정을 반복한다.
Solution
int numSubarrayProductLessThanK(int* nums, int numsSize, int k) {
int len=1;
int l,r;
l=r=0;
int mul=nums[0];
int ret=0;
while (1){
if (mul<k){
ret+=len++;
r++;
if (r>=numsSize) break;
mul*=nums[r];
}
else{
l++;
mul/=nums[l-1];
len--;
if (l>r) {
r=l;
len=1;
if (r>=numsSize) break;
mul=nums[l];
}
}
}
return ret;
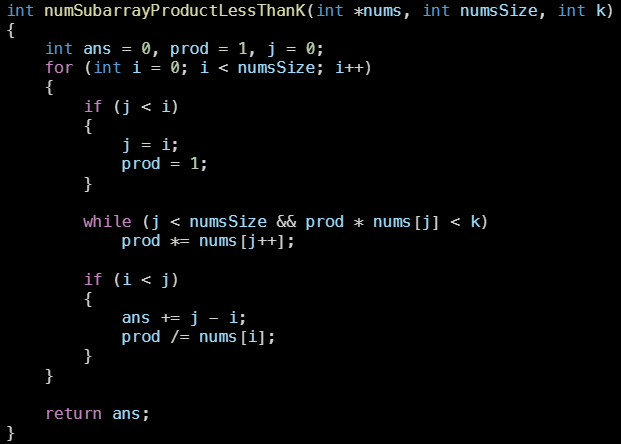
}교수님 풀이
내가 r이 변할때마다 매번 len의 길이를 output에 더했던 것과 달리, 교수님은 l이 변하기 전까지 r을 계속 움직인 다음 한 번에 len의 길이를 더했다.(l이 변할때마다 output에 더했다.)
Complexity
Time Complexity
두개의 포인터가 기껏해야 배열을 일순하는 것 밖에 없다.
Space Complexity
