이번 차수에서는 우리는 과연 우리가 학습시키는 알고리즘이 제대로 동작하는 지 확인하는 법에 대해서 알아볼 것이다.

Evaluating a Model

2가지의 feature을 갖는 데이터에 대해서 분류할 때, 우리는 그래프를 그려서 이게 제대로 분류가 되고 있는 건지, overfitting되지는 않았는 지를 파악해 보았는데,

우리는 4차원 이상부터는 그래프로 도식화하여 확인하는 것이 어렵다. 고로, 4개 이상의 feature가 존재할 때 이 데이터에 대해서 overfitting이 발생하였는 지, 학습은 잘되었는 지 확인하는 방법에 대해서 알아봐야한다.

우리는 지금까지 전체 데이터 셋에 70%는 training set으로 30%는 test set으로 규정하였다.

그리고 training set으로 학습을 시키고 test set으로 평가를 하였다.

평가를 할 때는 regularization을 제외하고 식을 쓴다.

training data set에서 평가를 진행하기에는 그냥 답을 보고 배껴진 시험지를 채점하는 것 처럼 의미없는 일이라고 보여진다.

그럼 어떻게 하면 좋을까?

Model selection and training/cross validation/test sets

그래서 우리는 전체 데이터 셋에서 60%를 training set으로 20%를 cross validation set으로 나머지 20%를 test set으로 둔다.

• Training error: $J_{train}(\vec w, b)=\frac{1}{2m_{train}}[\sum^{m_{train}}_{i=1}(f_{\vec w,b}(\vec x^{(i)})-y^{(i)})^2]$
• Cross-validation error: $J_{cv}(\vec w, b)=\frac{1}{2m_{cv}}[\sum^{m_{cv}}_{i=1}(f_{\vec w,b}(\vec x^{(i)})-y_{cv}^{(i)})^2]$
• Test error: $J_{test}(\vec w, b)=\frac{1}{2m_{test}}[\sum^{m_{test}}_{i=1}(f_{\vec w,b}(\vec x^{(i)})-y_{test}^{(i)})^2]$

원래는 Test error만 보고 어떤 모델(w, b 값)을 고를 지를 결정했지만, 이제는 위의 3개 error를 보고 선택한다.

Diagnosing bias and variance

• High bias => under fit(모델이 너무 단순해서 학습 자체가 제대로 이루어지지 않았다는 말) => $J_{train}$이 높고, $J_{cv}$도 높음.
• High Variance => over fit(모델이 너무 복잡해서 특정한 데이터 셋에 맞게 학습된 것) => $J_{train}$은 낮고, $J_{cv}$는 높음.

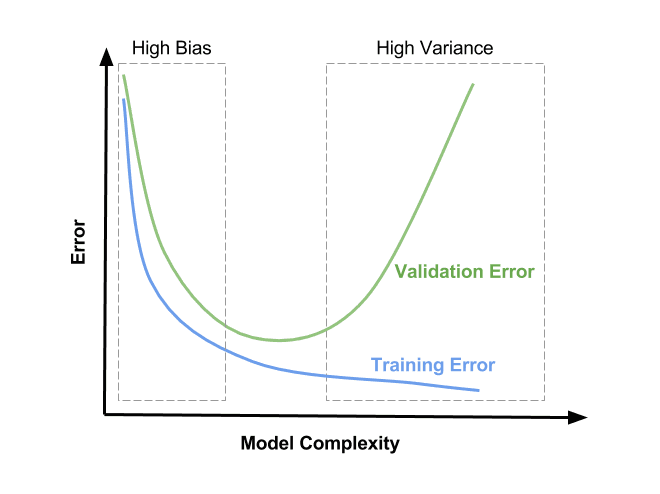
-> 이런 식으로 특정 구간에 들어가면 training error와 validation error사이에 trade-off가 발생한다.

$\therefore$ high bias이고 high variance이면 아주 최악인 거임.

Regularization and bias variance

우린 이전에 정규화를 통해서 overfitting을 해결해준다고 했다.

그럼 lambda의 설정이 bias와 variance에는 어떤 영향을 끼칠까.

• $f_{vec w, b}=w_1x + w_2x^2+w_3x^3+w_4x^4+b$
• $J_{(\vec w, b)}=\frac{1}{2m}\sum^m_{i=1}(f_{\vec w,b}(\vec x^{(i)})-y^{(i)})^2+\frac{\lambda}{2m}\sum^n_{j=1}w_j^2$
• $\lambda$ = 10,000이면, 가중치의 값이 너무 작아져서 거의 선형 방정식과 유사하게 되버리기에 bias가 높아진다. underfit 발생.
• $\lambda$ = 0이면, 너무 작아서 애초에 정규화를 하지 않은 것과 같다고 볼 수 있다. 그럼 variance값이 높아져서 overfit 발생.

고로, 우리는 적당한 $\lambda$값을 찾기 위해서 validation set을 이용한다.
cross-validation set을 이용하여 $J_{cv}(w,b)$를 구하면 어떤 lambda값이 적당한 지를 파악할 수 있음.

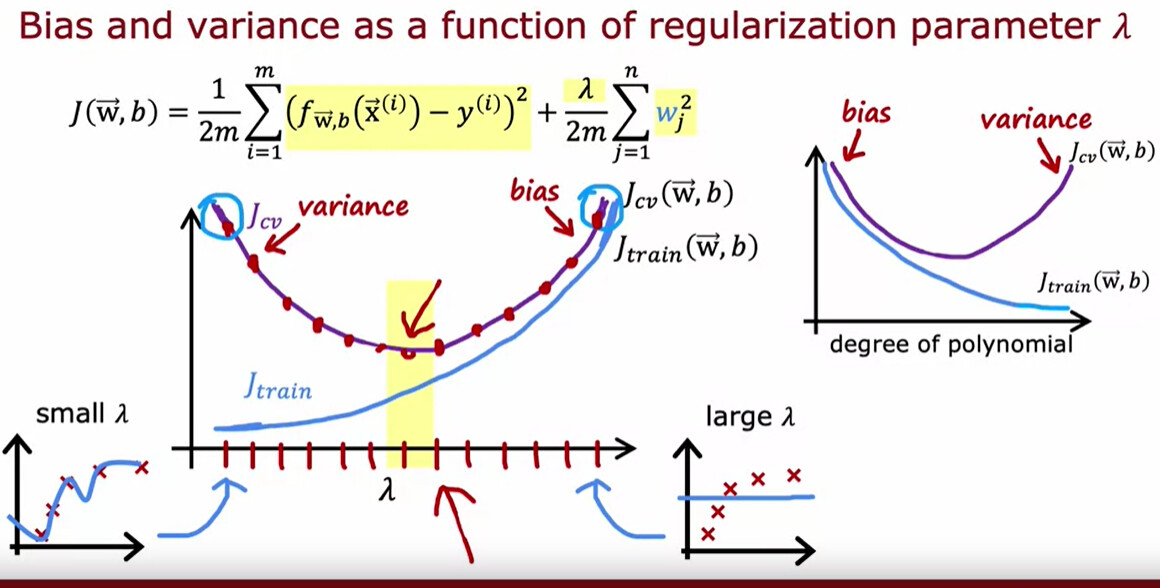
이런 식으로 lambda에 대해서는 위에서 봤던 그래프를 세로축을 기준으로 반대로 뒤집은 그래프가 나오게 된다.(당연한게 lambda는 모델의 복잡도를 낮추기 때문이다.)

Establishing a baseline level of performance

이제는 우리는 human level performance라는 것에 대해서도 생각할 것이다.

간단하게 생각해서 우리는 지금 껏 training error, validation error, test error 모두 인공지능의 성능에 대해서만 생각했다.

하지만, 데이터 자체에 문제가 있어서 사람도 제대로 구분하지 못하는 데이터일 수도 있다는 것도 우리는 고려를 해야한다.(ex. 너무 이미지가 흐려서 이게 무슨 이미지인 지를 잘 모르는 것)

결국,

• Human level <-> Training error: Bias
• Training <-> Cross Validation error: Variance

라고 볼 수 있다.

Learning curve

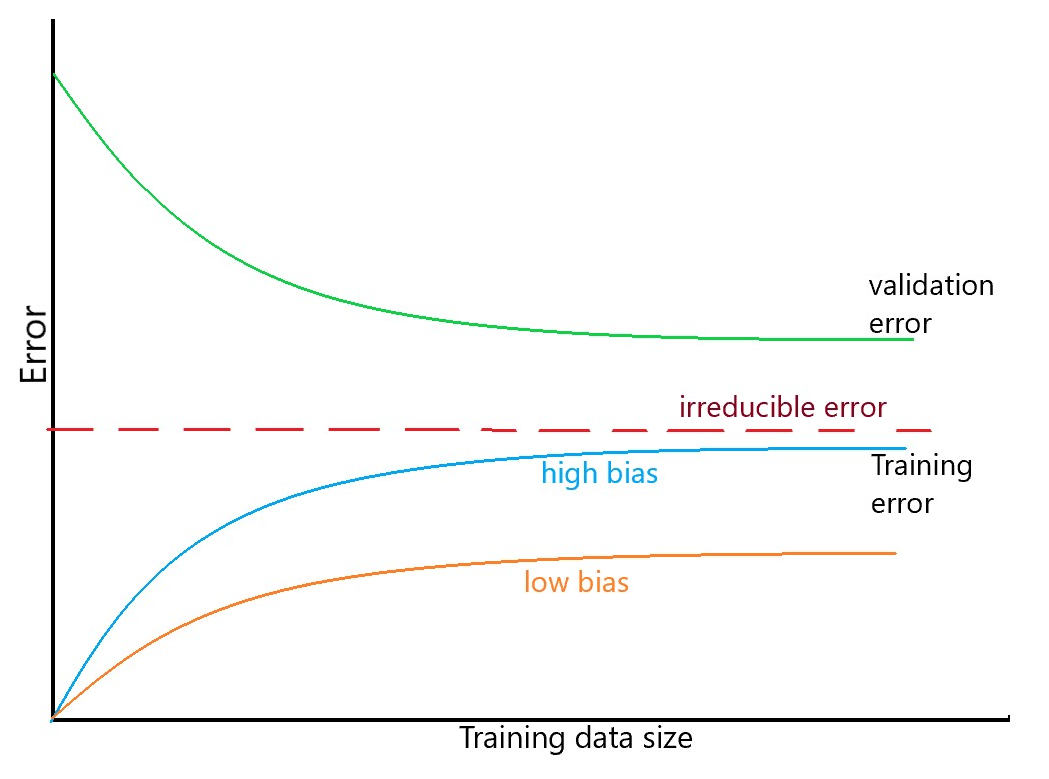
위의 이미지를 보면, 우리는 정규화 방법을 제외하고 어떻게 overfitting에서 벗어날 수 있는 지가 적혀있다.

간단한게 data set을 더 추가하면 된다. 여기서 데이터셋을 추가할 수록 training error는 증가하는 것을 볼 수 있는데, 당연히 더 데이터가 많아지면서 training할 것도 많아지기 때문이다.

한마디로, high variance한 경우는 데이터를 추가하는 게 도움이 되지만, high bias의 상황에서는 데이터를 추가하는게 그닥 도움이 안된다는 것을 알 수 있다.

Deciding what to try next revisited

그럼 이제 우리는 모델이 오류를 발생했을 때, 고려해야하는 것들을 정리해볼 수 있다.

• 더 많은 훈련 data 가져오기 => high variance에 도움
• 더 작은 feature 집합들을 시도하기 => high variance에 도움
• 추가적인 feature들 얻어오기 => high bias에 도움
• 다항 feature들을 추가하기 => high bias에 도움
• $\lambda$를 줄여보기 => high bias에 도움
• $\lambda$를 늘려보기 => high variance에 도움

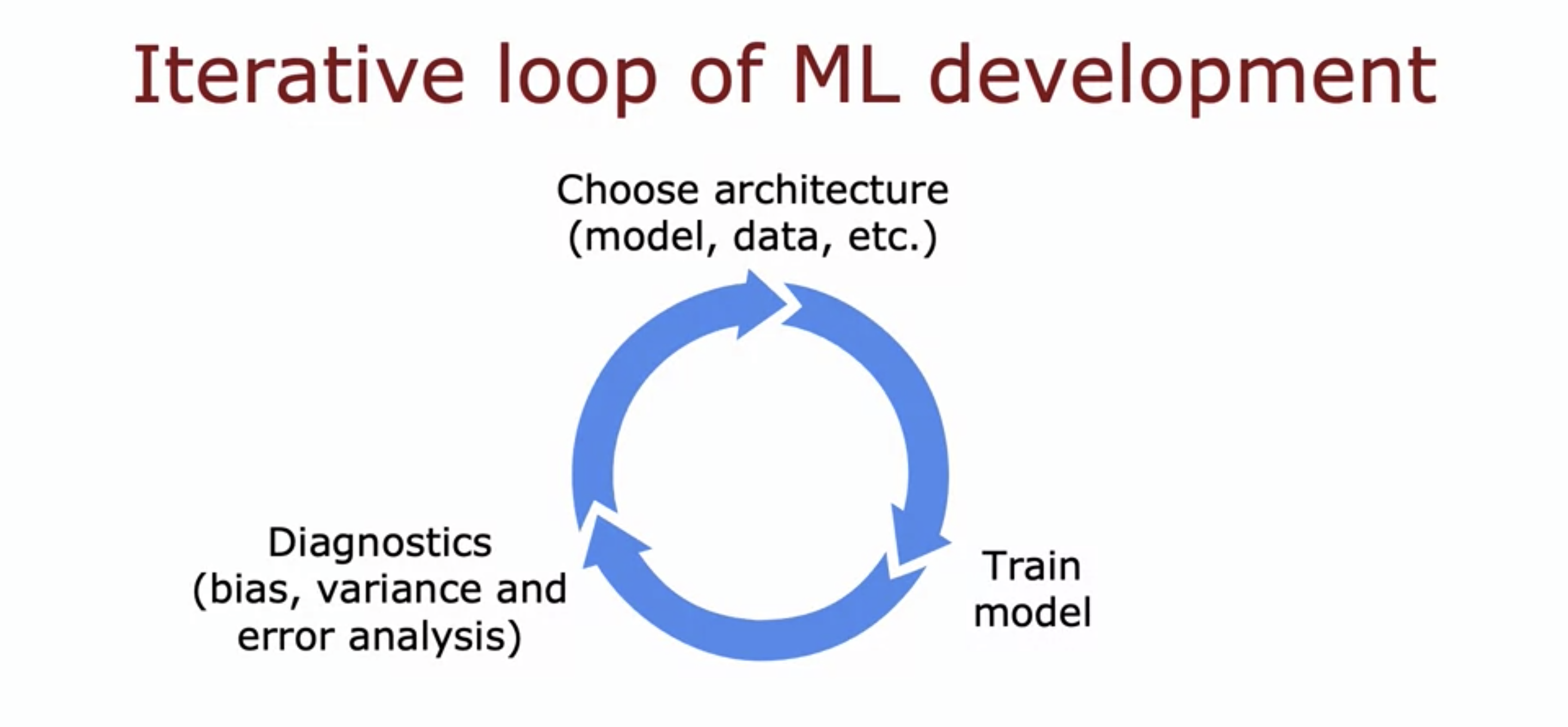
이러한 순환 구조에서 우리는 이런 개념들을 생각하면서 계속 모델들을 향상시켜나간다.

Adding Data

Data Augmentation과 Data synthesis를 사용하여 데이터의 수를 더 증가시킬 수 있다.

Transfer Learning: using data from a different task

Transfer Learning은 전이 학습 이름 그대로, 이미 학습되어있는 모델을 가져와서 새로운 데이터를 위해 사용하겠다는 의미이다.

여기에는 2가지 방법이 존재하는데,

1. 새로운 데이터로 원래 있던 w, b 값을 그대로 가져오고 경사하강법 or Adam opt를 사용하여 마지막 layer의 w와 b값만 학습시킨다. => Supervised pretraining
2. 원래 있던 w,b의 값으로 전체 network의 w와 b값을 초기화 시킨다. 위랑 다른 건 학습 할 때 마지막 layer만 학습시키는 게 아니라 전체 network를 새로운 데이터에 맞게 다시 재학습 시킨다.
   => fine-tuning

** 이게 어떻게 동작할 수 있는 거지? 이미지를 예로 들어보면, 이미지의 특성상 Edge, Corner, Curve가 있는데, 이미 많은 데이터로 이러한 특징 정보들에 대해서 잘 학습이 되어있어서, 원래 학습시던 이미지와 다른 종류의 이미지를 전이 학습을 시키면 처음 부터 하는 것보다 더 좋은 성능을 낼 수 있는 것이다.

(전이 학습할 때 입력 이미지 유형이 동일 해야함(Width x Height x channel 값)

Error metrics for skewed datasets

이 개념을 좀 더 직관적으로 파악하기 위해, 암을 예로 들어보겠다.

만약 100명의 사람중에 90명의 사람이 정상이고, 10명이 암에 걸린 경우가 있을 때
우리가 만든 모델이 그냥 100명의 사람 모두를 정상으로 체크했다고 하면, 90%의 성능을 보일 것이다.
하지만, 과연 이걸 제대로 된 성능이라고 볼 수 있을까? 만약 이게 좋은 성능이라고 한다면, 그냥 복잡한 알고리즘을 사용하지 않고 100명 모두 정상이다라는 출력을 주는 코드 몇줄을 적는 거와 다름이 없을 수 있다.

고로, 우리는 이러한 상황을 고려할 수 있는 평가 지표를 생각해봐야한다.

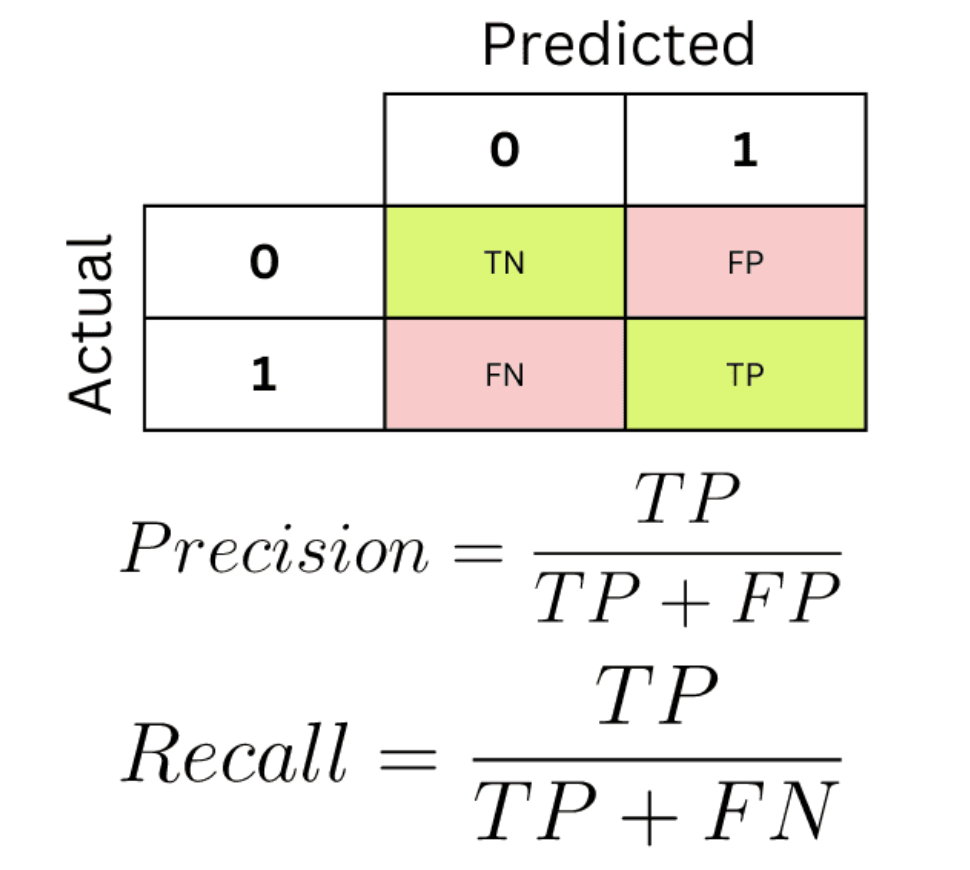
그걸 고려해서 나온, 평가 지표가 위에 보이는 metrics이다.

• TP(True Positive): 내가 Positive라고 예측했는데, 실제 값도 Positive인 경우(암이라고 예측했는데, 진짜 암인 경우)
• FP(False Positive): 내가 Positive라고 예측했지만, 실제 값은 Negative인 경우(암이라고 예측했는데, 정상인 경우)
• ...(위와 같은 방법으로 4 구역으로 나뉜다.)

그럼 이걸 이용해서 어떻게 성능을 평가할까? => Precision과 Recall 이용

• Precision: $\frac{\text{True Positive}}{\text{the number of predicted positive}}$ = $\frac{TP}{TP+FP}$
  => 내가 참이라고 했을 때, 진짜 참의 비율(암이라고 예측했을 때, 그 예측한 애들 중 진짜 암이었을 비율)
• Recall: $\frac{\text{True Positive}}{\text{the number of actual positive}}$=$\frac{TP}{TP+FN}$
  => 실제 참인 애들 중, 내가 참이라고 말한 애들의 비율(실제 암에 걸린 사람들 중, 내가 맞춘 사람들의 비율)

이 2개를 고려하면, 과연 이 모델이 무지성으로 그냥 한줄로 찍은 건지 아니면, 고려를 하고 답을 예측한 것인지를 파악할 수 있다.
만약에 한줄로 찍으면, precision과 recall 중 하나는 0이 되기 때문이다.

F1 score같이 이 2개를 활용해서 식으로 정리하는 방법도 존재한다.

요약하자면, 직관적으로 이러한 수치를 비교해서 우리는 데이터의 imbalance를 확인해볼 수 있다.

Trading off precision and recall

사실 precision과 recall 사이에는 trade-off가 존재하는데,

• 1: if $f_{\vec w,b}(\vec x)\geq threshold$

• 0: if $f_{\vec w,b}(\vec x)< threshold$
  => 여기서 threshold값을 높이면 예측 값중 1의 개수가 줄어들어서 precision이 증가하고 recall이 감소한다. 반대로 내리면 recall이 증가하고 precision이 감소한다.

• F1 Score => precision과 recall을 비교하는 방법. 그냥 둘의 average로 비교하는데 에는 무리가 있기에 조화 평균을 사용하여 비교한다.
  => $2*\frac{precision*recall}{precision+recall}$
  그럼 왜 조화 평균을 사용할까? 이전에 말했던 것 처럼 precision이나 recall 둘 중 하나의 값이 0이 되면 별로 좋은 값이 아니다. 고로, 조화 평균을 사용하여 둘 중 더 작은 값에 영향을 많이 받게 하기 위함이다.