우리는 이제까지 activation function에 대해서 sigmoid function만 알아봤지만, 더 다양한 activation function이 존재한다.

Alternatives to the sigmoid activation

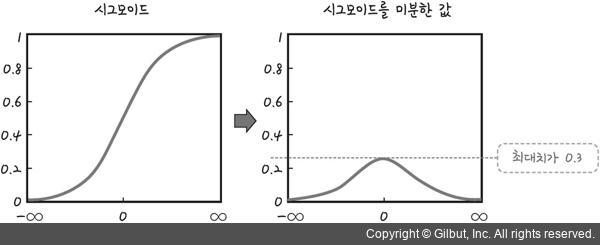
sigmoid 함수는 이분법적으로 나타내기에 좋은 함수이지만, 만약에 x축의 값이 너무 커지거나 작아지면 기울기가 0으로 수렴하게되는데, 이건 나중에 알게될 back propagation의 기울기 소실 문제와 연관이 있어 우리는 다른 activation function을 사용한다.

그 중에 가장 자주 쓰이는 activation function은 ReLU라는 활성화 함수이다.

• $g(z)=max(0,z)$

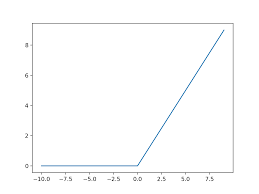
이라는 수식으로 나타난다.

ReLU함수는 입력 값이 양수인 경우에는 그래도 기울기를 가지고 있기에 sigmoid보다는 기울기 소실 문제를 해결할 수 있지만, 음수의 입력값에 대해서는 0이므로

Leaky ReLU라는 활성화함수도 사용하곤 한다.

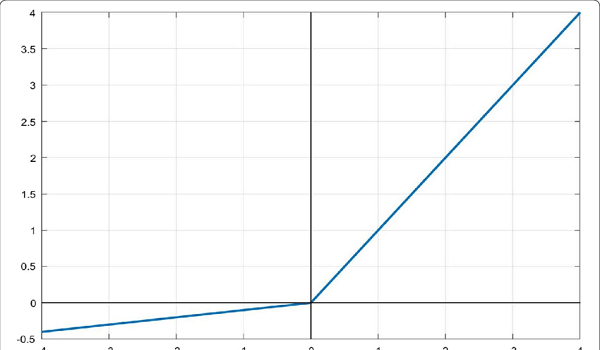
출력 계층의 활성화 함수는 label y에 따라 달라진다. 즉 이전에 말했던 것 처럼 우리가 어떤 결과를 받고 싶은 지에 따라 달라지는 것이다.

• Binary Classification => sigmoid function(y=0/1)
• Regression => Linear function(y=+/-), ReLU( y=0/+)

이전에도 말했던 것 처럼 Sigmoid 보다 ReLU가 좋다. 더 빠름.

그럼 우리는 왜 활성화 함수를 사용해야하는가?

사실 이것도 앞에서 말했었는데, 현실의 문제들은 생각보다 더 복잡하고 그것들을 해결하기 위해서 선형적인 해결은 어렵다.

그리하여 비선형적인 방식이 필요한데, 그걸 위해서 바로 활성화 함수들이 필요한 것이다.(너무 단순한 설명이라 이해가 안되다면 구글링으로 좀 더 깊은 탐색을 추천한다.)

Multi Class

지금껏 우리는 0과 1로만 분류하는 이진 분류(binary classification)만을 진행해 왔는데, 지금부터 다중 클래스에 대해서 분류는 어떤 식으로 해야하는 지 알아보자.

• $p(y=1|\vec x), p(y=2|\vec x), p(y=3|\vec x), p(y=4|\vec x)$
  이렇게 다중 클래스에 대해서도 분류를 할 수 있어야한다. 다중 클래스라고 하는 이유는 결과값 y의 값이 3개 이상으로 나오기 때문이다.

이걸 어떻게 해결할 수 있을까? => 여기서 나오는게 softmax 활성화 함수이다.

softmax를 사용하면 softmax regression alogrithm을 사용할 수 있는데, 이건 어떻게 보면 Logistic regression의 일반화라고도 볼 수 있다.

Softmax

Logistic Regression에서의 활성화 함수는 sigmoid 함수로 0과 1
2개로만 분류가 가능했는데,

• $a=g(z)=\frac{1}{1+e^{-z}}=p(y=1|\vec x)$

Softmax 활성화 함수를 사용하면,

• $z_i=\vec w_i\cdot \vec x+b_1, \text{ } a_i = \frac{e^{z_i}}{\sum^n_{i=1}e^{z_i}}$
• n: multiclass의 개수(y=1,2,3,...n)
• $a_1+a_2+...+a_n=1$(한 분포에 있는 확률이기에)

그럼 이제 Cost function은 어떻게 변했을 지를 살펴보자.

Logistic Regression

• $z=\vec w\cdot \vec x +b$
• $a_1 = g(z)=\frac{1}{1+e^{-z}}=p(y=1|\vec x)$
• $a_2 = 1 - a_1$
• $loss = -yloga_1-(1-y)log(1-a_1) = -yloga_1 -(1-y)loga_2$
• 첫째 항은 y=1일 때, 두번째 항은 y=0일 때

Softmax Regression

• $a_1=\frac{e^{z_1}}{e^{z_1}+e^{z_2}+...+e^{z_n}}=p(y=1|\vec x)$
  ...
• $a_n=\frac{e^{z_n}}{e^{z_1}+e^{z_2}+...+e^{z_n}}=p(y=n|\vec x)$
• $loss(a_1,...,a_n,y)= -loga_1,\text{if y=1}, \text{ } -loga_2,\text{if y=2}...-loga_n,\text{if y=n}$$,
• $if \text{ } y=j, -loga_j$ 결국 loss 값을 최소화 시키기 위해 $a_j$이 1에 가까워지도록 학습하는 거임.

Neural Network with Softmax output

output layer에서 몇개의 클래스를 구분할 것인지에 따라 output layer의 unit(neuron)의 개수가 정해진다.(ex. 0~9개의 숫자를 구분하는 거면 10개의 output layer)

• $z_1 = \vec w_1\cdot \vec a+b_1$, $a_1=\frac{e^{z_1}}{e^{z_1}+...+e^{z_10}}=p(y=1|\vec x)$
• ...
• $z_10 = \vec w_10\cdot \vec a+b_10$, $a_10=\frac{e^{z_10}}{e^{z_1}+...+e^{z_10}}=p(y=10|\vec x)$
• $\vec a=(a_1,...,a_{10}) =g(z_1,...,z_{10})$
• Loss function: Sparse Categorical Cross Entropy => label이 정수인 경우에 사용한다.

Multi_Class Classification과 Multi_label Classification

이 두 문제는 이름부터 혼동되기는 하지만, 간단하게 생각해서 Multi Class Classification은 softmax함수를 사용하고, Multi Label Classification은 sigmoid를 사용한다.

먼저 Multi Class에서 softmax를 사용하는 이유는 하나의 이미지에 하나의 object가 존재하여 지금 이 이미지에 어떤 오브젝트의 softmax값이 가장 큰 지를 파악해서 분류한다.
한마디로 모든 클래스에 대한 확률의 합은 1이 되는 것이다.

Multi Label은 하나의 이미지에 다양한 object가 있는데, 이러한 경우 threshold 값을 정해두고 이 값을 넘으면 있다고 분류한다. 여기서 softmax를 사용하게 되면 모든 클래스의 확률값의 합은 1이되므로 이상하게 된다. 고로, sigmoid를 사용하여 개별적용시켜서 분류해줄 수 있다.

Advanced Optimization

우리는 지금 껏 손실함수를 최적화 시키기위한 방법으로 gradient descent만 봐왔다.

하지만, 실제로는 다양한 최적화 방법이 존재한다.

• RMS Prop
  • 기울기가 과하게 커지면 기울기를 줄여주는 방식
  • 매개변수에 대해 개별적인 학습률을 적용 => 큰 그래디언트를 가진 매개변수의 학습률은 감소하고, 작은 그래디언트를 가진 매개변수의 학습률은 증가
  • 더 빠르고 안정적인 수렴 도모
  • 비등방성 문제를 해결
• Momentum
  • 이전 기울기들의 누적 평균을 현재 gradient descent에 반영
  • 학습 과정을 가속화 불필요한 진동을 줄여 local optimzation에 빠지는 걸 방지해줌.
• Adam Optimizer
  • RMS + Momentum
  • 1차 모멘텀(평균)과 2차 모멘텀(비분산)의 추정치를 모두 사용.