[Coursera] Supervised Machine Learning: Regression and Classification(1)

홍건하·2025년 4월 27일

Coursera machine learning

처음 Machine Learning 공부를 접하는 사람들에게 coursera의 Machine Learning Specialization를 추천해주고 싶다.

사실 나도 처음에는 boot camp에서 DeepLearning Sepcialization을 먼저 접해서 알게 되었지만, 위의 강의가 좀 더 처음 하시는 분들에게는 친절하게 설명해주는 것 같다.

먼저, Machine Learning 이란 무엇일까?

문제 상황에서, 사람은 바로 문제에 대한 답을 꺼내줄 공식을 찾는다.

Machine Learning은 이러한 공식을 기계가 스스로 찾을 수 있도록 하는 것이라고 볼 수 있다.

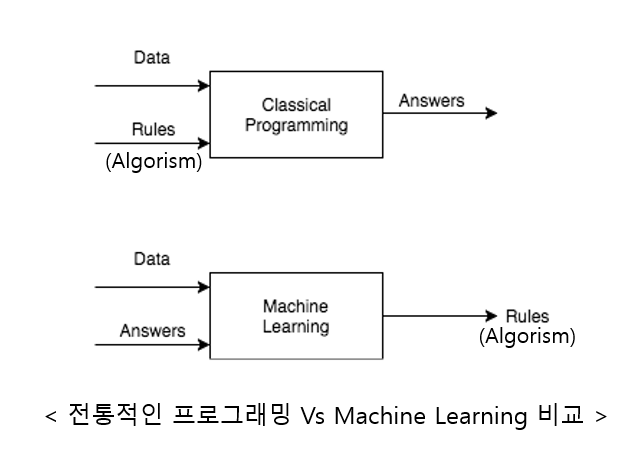
이런 식으로, 바로 문제를 해결할 Algorithm을 짜는 것이 아닌, Algorithm을 짤 수 있도록 프로그래밍하는 것을 Machine Learning이라고 한다.

이러한 Machine Learning에도 다양한 종류가 있는데,

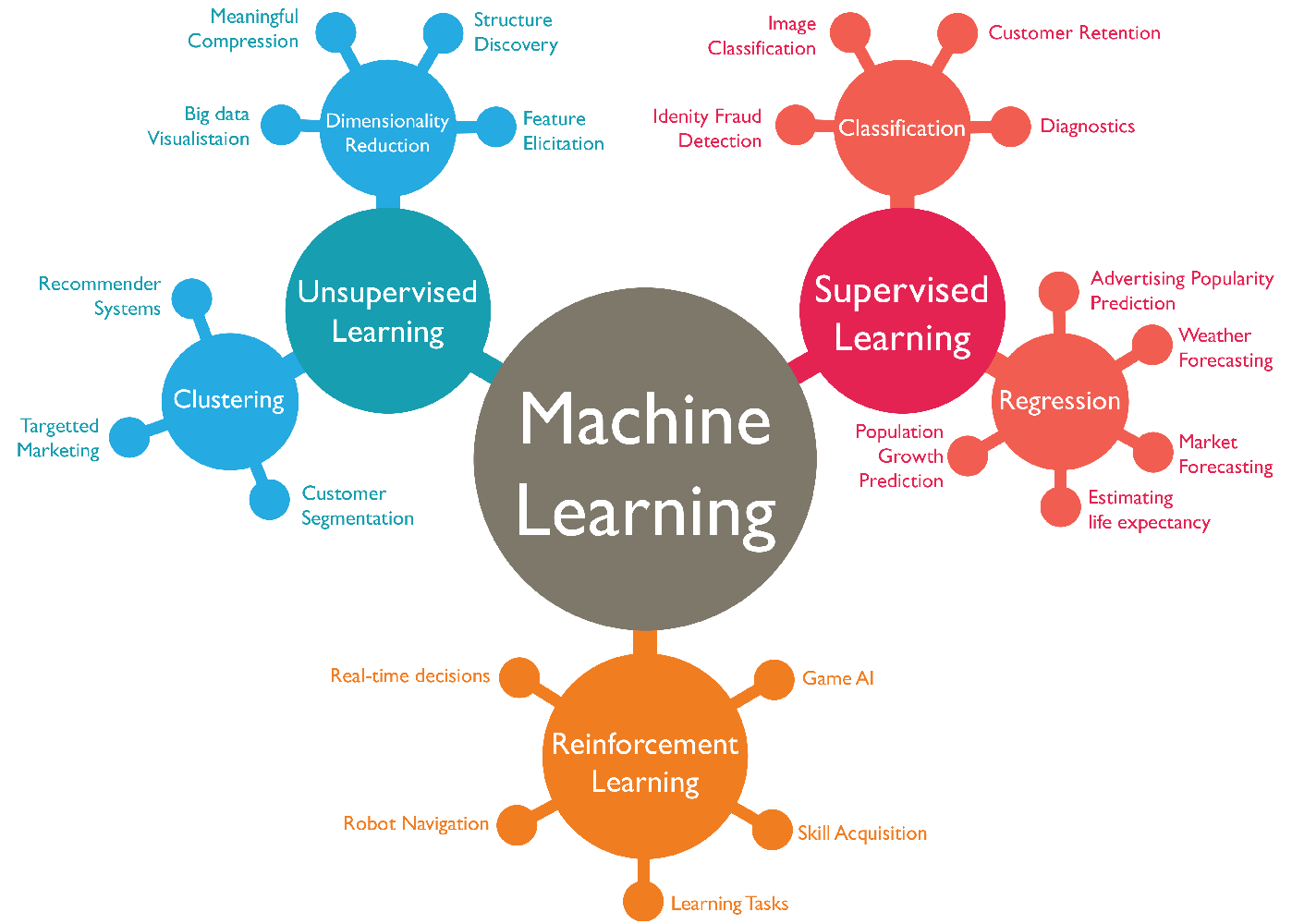
Supervised Learning: 직접 답안지를 주고, 그 답안지와 비슷한 답을 낼 수 있도록 학습시키는 방법(ex. Regression, Classification)
Unsupervised Learning: 답안지를 주지않고, 데이터만 주고 학습시키는 방법(ex. Clustering, Dimensionality Reduction)
Reinforcement Learning: 이것 또한, 답안지는 주어지지 않고 컴퓨터가 직접 경험하면서 총 보상을 최대화하는 방법을 선택하도록 학습하는 방법이다.

이렇게 대표적으로 3가지 방법이 있다.

이 중에, 우리는 먼저 Supervised Learning에 대해서 알아보자.

Supervised Learning

Supervised Learning은 정말 간단하게 말해서, x(input)-y(label)쌍을 학습하고 이전에 본적없는 x(input)가 들어오면 적절한 output(y)를 출력하는 것이다.

이 방법도 2가지 case로 분류할 수 있는데,

Regression(회귀): 무한의 가능한 수의 출력에서 숫자를 예측(ex. 집값 예측)
Classifciation(분류): 유한히 가능한 수의 출력에서 category를 예측하는 알고리즘(ex. 암에 걸렸는 지 유무 판단)

Classification

=> 0,1과 같이 작은 유한한 가능한 output의 집합에서 예측한다.(여기서 category는 꼭 0,1과 같은 숫자일 필요는 없다. but 0.5나 1.75같은 무한한 실수를 사용하지는 않음.)

input: x (데이터의 feature, ex. 귀, 코, 눈 etc..)
output: y (데이터의 label, Ex. 고양이(0), 개(1))

Regression

=> 데이터의 feature들을 살펴보고, 이 데이터가 어떤 y값을 갖을 지를 예측하는 알고리즘.

input: x (데이터의 feature, ex. 방의 크기, 높이, 방의 개수 etc..)
output: y (데이터의 label, Ex. 1억 4천만원, 2억 3천만원, 1억 8천만원...)

Classification와는 다르게 출력이 집합안에서 발생하는게 아님.

Unsuprevised Learning

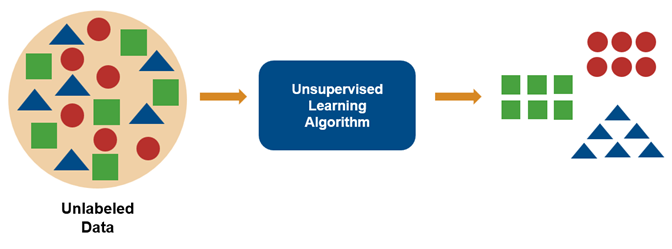
Unsupervised Learning은 label이 없다. 즉, 정답을 입력으로 받지 않는 다는 것이다.

그럼 얘는 왜쓸까? 라는 의문이 생길 텐데, 가장 크게 보면 데이터의 구조를 파악하고자 사용한다.

우리는 Unsupervised Learning을 통해서 서로 비슷한 데이터끼리 묶을 수도 있고, 차원이 너무 높은 데이터(ex. 이미지)를 차원이 낮은 데이터(ex. vector)로 바꿀 수 있다.

Clustering: 비슷한 data point끼리 묶는 것.
Anomaly detection: 특별한 data point들을 찾는 것(너무 동떨어진 데이터는 Noise로 간주되기 때문에)
Dimensionality Reduction: 정보 손실을 최소화하면서 data set을 축소시키는 것

여기까지가 Machine Learning의 큰 개념들이다.

요약하면

Machine Learning
- Supervised Learning
  - Classification
  - Regression
- Unsupervised Learning
  - Clustering
  - Anomaly Detection
  - Dimensionality Reduction
- Reinforcement Learning

으로 볼 수 있을 것 같다.(강화학습은 다음에 다루도록 하겠다.)

이 강의에서는 먼저, regression 모델 중 하나인 Linear Regression model에 대해서 설명한다.

Linear Regression Model

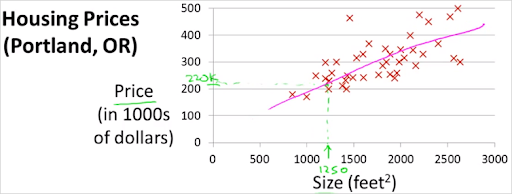
위에서 말했듯이, regression model은 입력값에 대해서 그에 해당하는 출력값을 예측한다. 이때, 출력값은 한정된 집합이 없다.(ex. 집 값 예측)

인공지능 모델을 학습시킬 때는, Training data set과 Test dataset이 나뉜다.

Traininig data set: 학습을 위한 데이터 셋,
- x: 입력 변수, feature, input feature등으로 불린다.
- y: 출력 변수, target variable
- m: training example의 개수
- (x,y): 하나의 training example(feature과 label(정답)으로 이루어져있다.)
- ( $x^{(i)},y^{(i)}$ ): i번째 training example

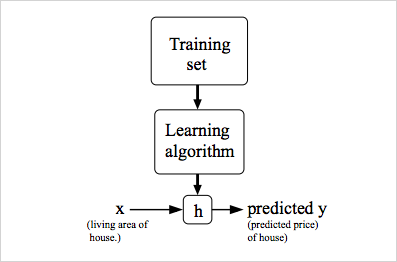
일단 Training set(featres, target)을 넣어주고 그걸 토대로 학습을 하여 f라는(위의 그림에는 h)function을 하나 준다.

그리고 그 fucntion을 통해 예측을 한다. 이게 기본 Mechanism이고,

여기서 fucntion은

$f_{w,b}(x)=w\cdot x +b$
w: 가중치, b: bias, x: 입력
-> 나중에 무엇인지 설명하겠지만, 여기서 b의 역할은 무조건 저 방정식이 (0,0)만을 지나지 않게 해줌. 표현력을 높여준다고 표현한다.

로 나타낸다.

이처럼 선형 방정식을 사용하기에 linear regression이라고 한다고 한다.

저런 방정식의 형태를 학습하여 새로운 x를 넣으면 그에 맞는 가격이 나와서 예측을 하게 되는 거임.

그럼 먼저 저 방정식을 좀 더 자세히 살펴보자.

Cost Function

model을 다들 정의하는 방법이 제각각이지만, 수식으로 표현하면,

$f_{w,b}(x)=w\cdot x +b$

이런 식이 나오는 것이다.

그럼 어떻게 학습이 일어나는 것이냐.

$\hat y^{(i)}=f_{w,b}(x^{(i)})=w\cdot x^{(i)}+b$

이렇게 i번째 값에 대해 예측할 수 있고, 이 예측값을 $\hat y^{(i)}$ 라고 한다.
그럼 우리는 실제값과 예측값의 차이를 줄여줘야하는데,

이때 조정되는 애들이 바로 w,b이다.

그리고 추가적으로, 우리는 실제값과 예측값의 차이를 계산하기 위해

$\frac{1}{2m}\sum^m_{i=1}(\hat y^{(i)}-y^{(i)})^2=J(w,b)=\frac{1}{2m}\sum^m_{i=1}(f_{w,b}(x^{(i)})-y^{(i)})^2$ (MSE, mean-squared-error라고 함)

로 표현한다.(여담으로 2로 나누는 이유는 나중에 미분할 때 수식을 깔끔하게 하기 위해서이다.)

고로, 우리의 목적은 $J(w,b)$ 를 최소화시키는 w와 b를 찾는 것으로 볼 수 있다. => $minimize_{w,b}J(w,b)$

좀 더 직관적으로 보기 위해서,

$\hat y^{(i)}=f_{w}(x^{(i)})=w\cdot x^{(i)}$

로 b를 제외하고 쓰겠다(b 값을 빼고 봐도 크게 상관은 없다고 한다.)

그러면 J식이

$J(w,b)=\frac{1}{2m}\sum^m_{i=1}(w\cdot x^{(i)}-y^{(i)})^2$

로 바꿀 수 있다.
이걸 그래프로 그려보면,

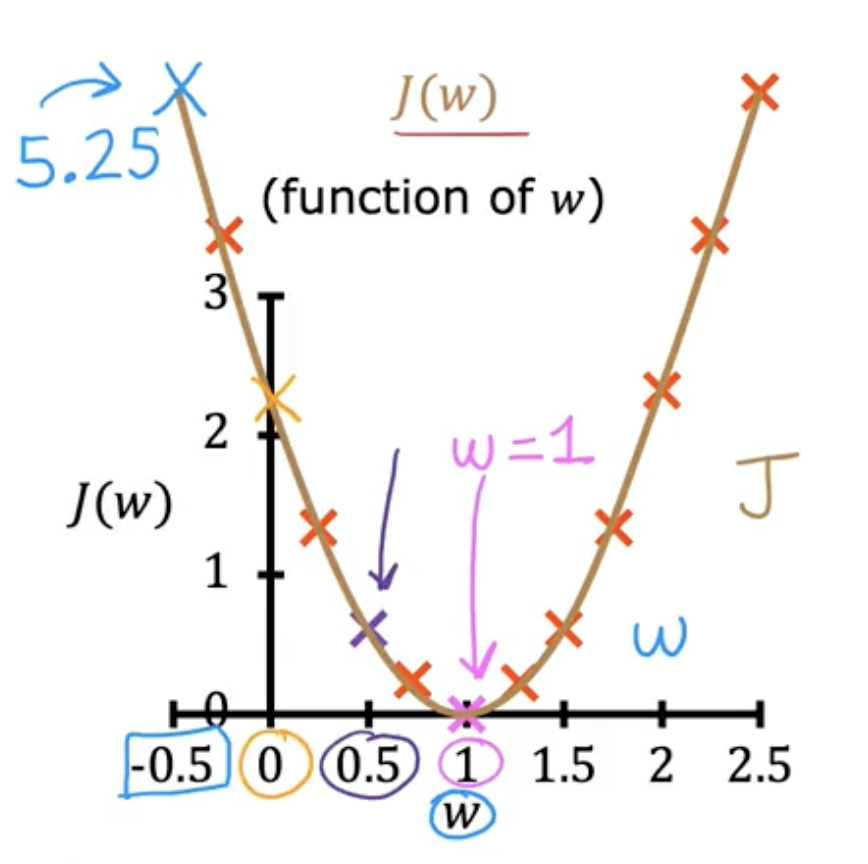
로 나타낼 수 있다.

이제 우리는 J의 최솟값이 되는 지점의 w를 찾아야하기 때문에(이게 학습에 목표이니까), 저 그래프의 최소점이 되는 w를 찾아야하는 것이다.

위의 그림으로 보면 찾기 쉽지만 실제 식은 훨씬 더 복잡하기 때문에 다른 방법을 사용한다.

Gradient Descent

그럼 어떤 방법을 사용해야할까? 이 방법에 대해 처음 듣게 되었을 때, 나는 인공지능이 좋아졌다.

우리는 경사 하강법이라는 방법을 사용할 것이다.

먼저 우리는 $minimize_{w,b}J(w,b)$ 에서 w와 b를 0으로 초기화하고 조금씩 바꿔서 J를 최소화 시킬 것이다.

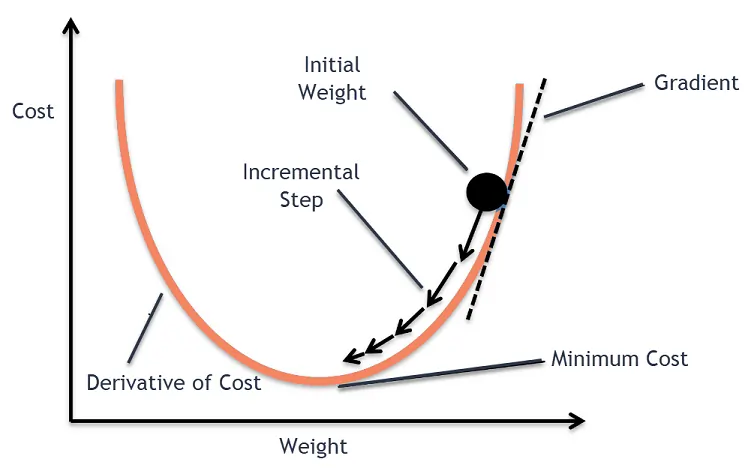
더 직관적으로 생각해보면, 위의 그림처럼 최소값으로 가기 위해서 우리는

$w=w-\alpha\frac{d}{dw}J(w,b)$
$b=b-\alpha\frac{d}{db}J(w,b)$

식을 사용할 것 이다.

$\alpha$ : Learning rate(학습률)
$\frac{d}{dw}J(w,b)$ : derivative(기울기)

를 뜻한다.

간단하게 말해서, convex(볼록한)그래프의 기하학적인 구조를 생각하면, 최솟값의 오른쪽에 있을 때는 기울기가 양수, 최솟값의 왼쪽에 있을 때는 기울기가 음수라는 점을 사용하여 최솟값에 이를 때까지 기울기 만큼의 값들을 빼줘서 최솟값에 이르는 w를 찾는 방식인 것이다.

여기서 learning rate는 쉽게 생각하면 내가 한번 이동할 때 얼마나 이동할 지의 크기라고 생각하면 된다.

Learning rate

Learning rate는 학습하여 구하지 않고, 우리가 직접 정해주는 값인데,(이렇게 우리가 직접 정해주는 값인데 parameter에 영향을 주는 값들을 hyper parameter라고한다.)

이 수치를 너무 작게 잡으면, 당연히 w의 이동량이 감소해서 수렴하는데 오래 걸린다.

하지만, 반대로 너무 크면, 한번 이동할 때, 최솟값 부분을 벗어나서 계속 진동할 수 도 있다.

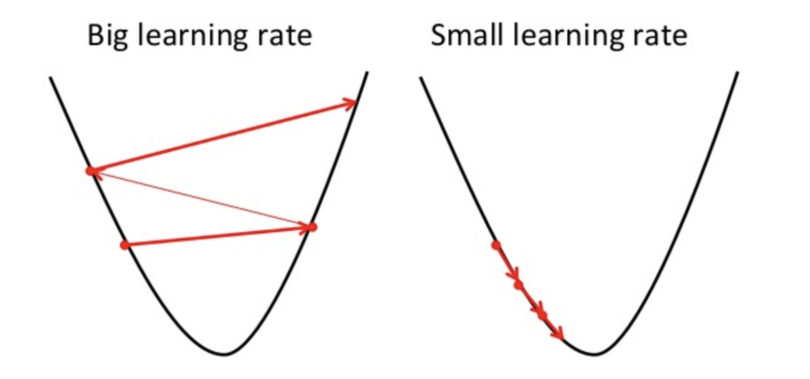
지금까지 Gradeint descent에 대해 간단히 알아봤다.

그럼 이제 우리가 처음에 본 linear regression model에서는 이걸 어떻게 적용하는 지 알아보자.

Linear Regression's Gradient Descent

일단 다시 모델 식에 대해서 살펴보면,

$f_{w,b}(x)=w\cdot x +b$
$J(w,b)=\frac{1}{2m}\sum^m_{i=1}(f_{w,b}(x^{(i)})-y^{(i)})^2$

위에는 모델 식, 아래는 손실 함수 이다.

그럼 이제 이 식들을 gradient descent 식에 대입 해보겠다.

$w=w-\alpha\frac{d}{dw}J(w,b)$ => $\frac{d}{dw}J(w,b)=\frac{1}{m}\sum^m_{i=1}(f_{w,b}(x^{(i)}-y^{(i)})x^{(i)}$
$b=b-\alpha\frac{d}{db}J(w,b)$ => $\frac{d}{db}J(w,b)=\frac{1}{m}\sum^m_{i=1}(f_{w,b}(x^{(i)}-y^{(i)})$