참고 자료: 초보를 위한 정보이론 안내서 - Entropy란 무엇일까

먼저, 아주 자세하게 설명을 해주신 위 주소의 주인분께 감사의 말을 전한다.

일단 Entropy에 대해서 알아보자.

Entropy

Entropy를 말하기전 과연 우리가 일상에서 말하는 정보와 정보량은 뭘 의미할까?

• 정보: 관찰이나 측정을 통해 수집된 데이터를 실제 문제에 도움이 될 수 있도록 해석하고 정리한 지식.
• 정보량: 어떤 내용을 표현하기 이ㅜ해 물어야하는 질문의 개수

뭔가 생각보다 직관적인 정의를 가지고 있어서 이해하는 데에 어려움이 없다.
Ex) 만약, 한 사람이 알파벳 글자중 하나를 선택했다. 그 글자를 맞추기 위해 우리는 최소 몇번의 질문을 해야할까?
최적의 방법은 아마 알파벳을 절반씩 나눠서 어느쪽에 포함되어있는 지를 묻는 방법일 것이다.(binary search) => 이러한 경우 4~5번만 질문하면 된다.
간단하게 구해보면

• $2^{\text{질문의 개수}} = 26$ -> $\text{질문의 개수} = log_226$

$\therefore$ 우리는 위의 방법을 사용하여 알파벳을 알아낼 때 최소 4.7개의 질문으로 어떤 알파벳을 선택했는 지 알 수 있는 것이다.

그럼, 6개의 알파벳 글자를 알기 위해선? => 당연히 6 x 4.7 = 28.2개의 질문이 필요할 것이다.

• $\therefore \text{질문 개수} = log_2(\text{가능한 결과의 수})$, 위의 6 알파벳의 경우 가능한 결과의 수는 $26^6$이 되기 때문이다.($log_226^6=28.2...$)

-> R.V.L Hartely에 따르면,

• $H=nlog(s)=log(s^n)$ (H: 정보(최소한 질문의 개수), n: 지금 보내는 문자열의 문자(글자, 숫자 etc) 개수(6개), s: 각 선택에서 가능한 결과의 가짓수(26개의 알파벳 수)

Entropy

이제 대충 정보에 대해서 감을 잡은 것 같으니, Entropy에 대해서 알아보자.

먼저, 문자열을 출력하는 기계 X와 Y를 가정해보겠다.

• X: A,B,C,D를 0.25의 확률로 출력
• Y: A(0.5), B(0.125), C(0.125), D(0.25)의 확률로 출력.

X가 출력한 글자가 뭔지 맞추기 위한 최적의 방법은 알파벳과 같이 A,B에 속하는 지 물어보고 속하면 A인지 물어보고 나머지도 같은 방법으로 하면 된다.
그럼, 총 최소 2번의 질문을 하면 어떤 글자인지 알 수 있게된다.

또한, 이걸 위의 수식으로 풀어도

• $H=1*log_2(4)=2$

로 풀어낼 수 있다.

하지만, Y의 경우는 위와 같이 간단하게 나타낼 수 없는데, 그 이유는 글자가 출력될 확률이 각각 다르기 때문이다.
즉, X를 알아냈을 때처럼 반절나눠서 포함이 되는 지 물어보는 건 최적의 방법이 되지 않는다.

Y의 경우에는 확률이 가장 높은 글자부터 확인을 하는 방법이 가장 최적의 방법이 될 수 있을 것이다.
이런 경우,

• A: 질문 1번
• B: 질문 3번
• C: 질문 3번
• D: 질문 2번

총 이렇게 물어보면 알아낼 수 있다. 그럼 이제 어떤 글자인지 최소의 질문 개수를 알아보기 위해선, 어떻게 해야할까?
=> 자신이 나올 확률에 자신이 나올 수 있는 질문의 개수를 곱해서 다 더하면 우리는 Y가 어떤 글자를 출력했는 지 알기위해 해야할 질문의 개수를 알 수 있다.

• $P(A)*1+P(B)*3+P(C)*3+P(D)*2=0.5*1+0.125*3+0.125*3+0.25*2= 1.75$
• X의 경우: $P(A)*2+P(B)*2+P(C)*2+P(D)*2=0.25*2+0.25*2+0.25*2+0.25*2= 2$

Y는 총, 1.75개, X는 총 2개의 질문이 필요하다.

Y 기계의 글자를 알아내기 위해선 1.75개의 질문을 X 기계의 글자를 알아내기 위해선 2개의 질문을 해야한다. => 이게 만약, 100글자라면 X: 200개, Y: 175개
$\therefore$ Y가 X보다 필요한 정보량이 적다.(Y가 X보다 불확실성(randomness)가 더 적기 때문이다. 모든 결과의 확률이 동일한 경우 불확실성이 가장 높다.)

이러한 불확실성의 측정을 Claude Shanon은 "Entropy"라고 부르기로 했다.

다시 문제를 돌아보면, 각 글자의 질문 횟수는 자신의 발생 확률과 연관된다.

• $A: 0.5=\frac{1}{2}, B:0.125=\frac{1}{8},C:0.125=\frac{1}{8},D:0.25=\frac{1}{4}$
• $log_2\frac{1}{\frac{1}{2}}=1, log_2\frac{1}{\frac{1}{8}}=3,log_2\frac{1}{\frac{1}{8}}=3,log_2\frac{1}{\frac{1}{4}}=2$

(참고로, 이러한 값은 결과가 0(거짓)아니면 1(참)만 나오는 경우인 이산확률 분포일 때만 성립한다.)

고로, 위의 값들을 일반화된 식으로 써보면

• $H=\sum\text{(사건 발생 확률)}\cdot log_2\frac{1}{\text{(사건 발생 확률)}}$ = $\sum_i p_i\cdot log_2(\frac{1}{p_i})$ = $-\sum_i p_i\cdot log_2(p_i)$

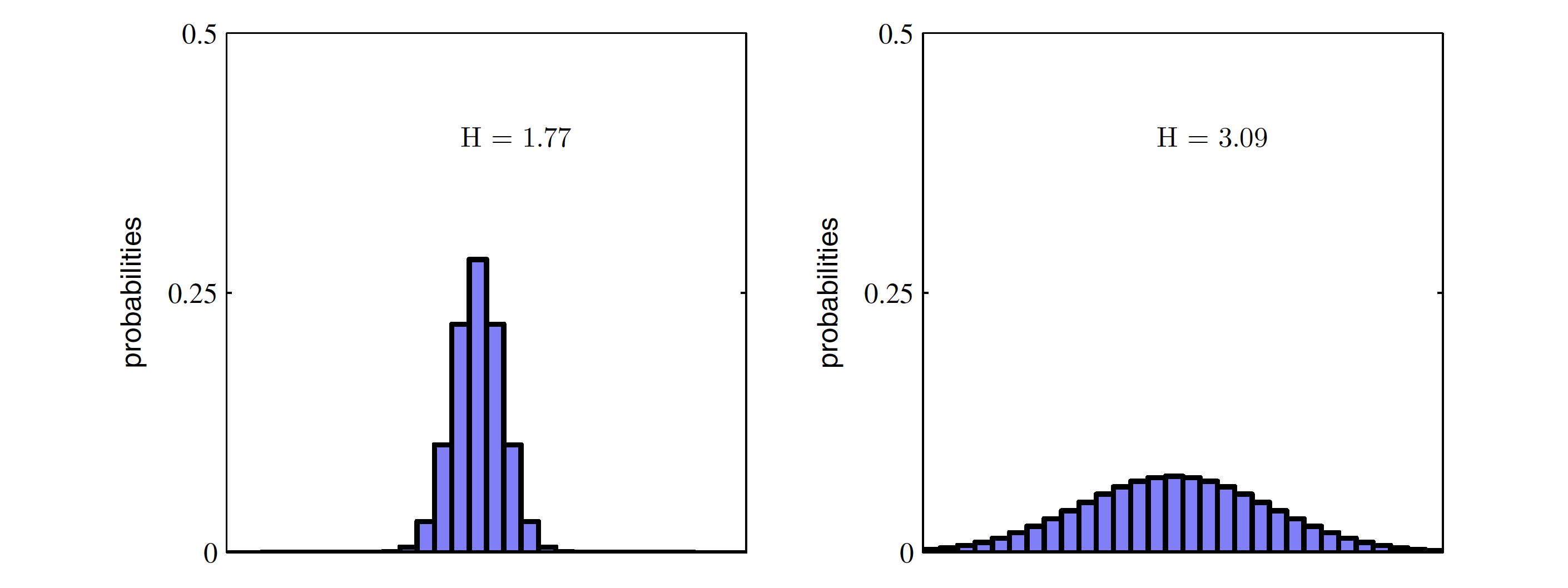
(다시, Entropy는 모든 사건이 같은 확률로 일어날 때(무작위성이 가장 높을 때) 그 최댓값을 갖는다. 왼쪽보다 오른쪽이 entropy가 더 높다.)

Entropy: 최적의 전략 하에서 그 사건을 예측하는 데에 필요한 질문 개수에 대한 기댓값

Entropy가 감소한다는 것은 사건을 맞추기 위해 필요한 질문개수가 적어진다는 것이고 이것은 정보량의 감소를 뜻한다.

Cross-Entropy

이전에 기계 X에 쓴 전략(절반 해서 포함되는 지 물어보기)을 Y에 적용해보면 어떨까?

결국, 우리는 정보량을 표현하기 위해 각 글자가 나올 확률에 글자를 알아내기 위한 질문 개수를 곱했었다.
근데 여기서 질문 개수는 결국 $log_2\frac{1}{\text{(사건 발생 확률)}}$ 이었으니,

기계 X에 쓴 전략을 Y에 적용한다는 말은 X가 각 글자를 뽑을 확률의 역수에 로그 2를 씌운 값(각 글자에 해당하는 질문의 개수)을 Y가 각 글자를 뽑을 확률에 각각 곱해서 더한 값을 구하는 것이라고 생각할 수 있다.

• $0.5 * 2+(0.125*2)*2+0.25*2 = 2$

이렇게 되면 기존의 1.75개의 질문 개수보다 0.25가 더 크다.

(여기서 나온 0.25가 cross entropy의 값이다.) -> 이렇게 생각해도 되나? 아래 괄호를 보니 가능할듯

Cross Entropy: 특정 전략을 쓸 때 예상되는 질문 개수에 대한 기댓값 => 확률 분포로 된 어떤 문제 p(Y 기계에서 각 글자가 나올 확률)에 대해 확률분포로 된 어떤 전략 q(X 기계에서 각 글자가 나올 확률)를 사용할 때의 질문 개수의 기댓값.

(최적의 전략을 사용할 때, cross entropy값이 최소가 된다. 즉 entropy값과 동일해진다.) => 이걸 생각해보면, 왜 cross entropy를 최소화 시키는게 진짜 확률분포에 가깝게 만드는 건 지 이해가 됨.

결국, cross entropy는 두 확률 분포의 차이를 구하기 위해 사용된다.
한마디로 원래의 Entropy에서 다른 확률 분포의 전략을 가져와서 구한 cross entropy값을 구해서 빼주면 확률 분포의 차이 or 정보 손실량이 나타나는 것이다.(사실 이걸 보면 좀 헷갈림)
근데 결국 cross entropy를 최소화 하는 방식으로 예측한 확률 분포를 최적화 하는데, 이 말은 결국 cross entropy를 진짜 분포의 entropy에 가깝게 만든다는 뜻과 동일하다.

• $H(p,q)=\sum_i p_i\cdot log_2\frac{1}{q_i} = -\sum_ip_i\cdot log_2q_i$
• $p_i$: 특정 확률에 대한 참값 or 목표 확률, $q_i$: 우리가 현재 학습한 확률

$\therefore q_i$를 학습하고 있는 상태면 $p_i$에 가까워질 수록 cross entropy 값은 작아지게 된다.

이산형 확률 분포에서는 $\sum$을 사용하지만, 연속 확률 분포에서는 $\int$를 사용한다.

• $-\int {p(x)\cdot logq(x)}dx$

잡생각: 결국 "전략"이라는 건 $log_2{\frac{1}{\text{(사건 발생 확률)}}}$ 인 건가.. 그리고 반대로 적용하면

• $0.25*1+0.25*3+0.25*3+0.25*2=2.25$
  
  이렇게 되는데 결국 생각해보면, 참값과 예측값 둘 중 어디서 빼든 확률 분포의 차이(정보 손실량)=0.25로 동일함. 한마디로 기준은 둘 중 누굴 선택하든 비슷함.

logistic regression의 손실함수를 생각해보면

• $-ylog\hat y-(1-y)log(1-\hat y)$

인데 이건 결국 cross entropy이다.

일단, $y\in \{0,1\}$ 이라는 가정하에
하나씩 보면,

• $q_{y=1}=\hat y$(어떤 대상이 1이라고 예측할 확률), $q_{y=0}=1-\hat y$(0이라고 예측할 확률)
• $p_{y=1}=y$(어떤 대상이 1일 확률), $p_{y=0}=1-y$(어떤 대상이 0일 확률)
• $\therefore p=[y,1-y], q=[\hat y, 1-\hat y]$

이렇게 놓고 보면, 위의 logistic regression의 식은 결국 H(p,q)를 한 것. 즉, cross entropy를 구한 것이라고 볼 수 있다.

좀 더 자세하게 들어가보면,
cross entropy는 log loss라고 부르기도 한다.
왜? => cross entropy를 최소화한다는 건 == log likelihood를 최대화하는 것이다.

y가 0또는 1 값만 가질 때, Likelihood를 구해보면

• $\hat y^y\cdot (1-\hat y)^{(1-y)}$ => y가 1이면, $\hat y$을 최대화, y가 0이면 $1-\hat y$를 최대화 시키면 된다.

저 위의 식에 log를 씌우면,

• $maximize(y\cdot log\hat y+(1-y)\cdot log(1-\hat y)=minimize-y\cdot log\hat y-(1-y)\cdot log(1-\hat y)$

이렇게 나타낼 수 있고, 이건 결국 cross entropy를 최소화하는 것과 동일하기 때문이다.

결국, cross entropy == log loss == negative log likelihood 라고 부를 수 있는 것이다.

---

이 개념을 통해서 우리는 정보를 수식적으로 나타낼 수 있게 되고, 정보의 불확실성 그리고 우리가 어떠한 문제의 정답을 알기위한 질문의 개수(정보량)을 측정할 수 있으며,

각 정보가 갖는 확률 분포의 차이를 나타낼 수 있게 되었다.