Activation function
-
이전 층의 출력 값에 적용시켜 다음 층의 뉴런으로 신호를 전달
-
모델의 복잡도를 올리기 위해 활성화 함수를 사용함, 선형 함수를 사용하면 hidden layer를 여러 겹 쌓는 의미가 없음, 출력 값이 단순히 선형 함수 여러 개를 합친 것이기 때문, 비선형 함수를 사용
Sigmoid
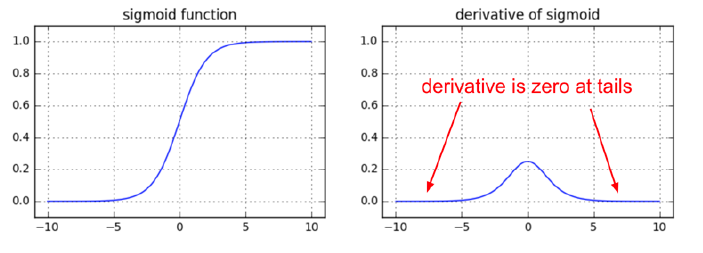
-
로지스틱 함수라고도 불림, (0,1), 입력 값이 작거나 커지면 기울기가 0에 수렴, 가중치 갱신이 되지 않아서 학습이 중단되게 됨
-
함수값 중심이 0이 아니라 모든 입력 값을 양수로 만듦, 오차 역전파 시 모든 가중치의 부호가 동일해지게 됨, 가중치 w1, w2가 있고 w1은 - 방향, w2는 + 방향으로 학습 되는 것이 최적일 때 w1은 - 방향으로, w2는 + 방향으로 가중치 갱신하는 것이 불가능함, w1 +, w2 +++ -> w1 ---, w2 - 식의 업데이트만 가능하여 zig-zag path로 수렴하기 때문에 수렴 속도가 느림
-
Exp 연산이 무거움
-
단점으로 인해 최근에는 잘 사용되지 않으나 classification task에서 종종 보임
Tanh
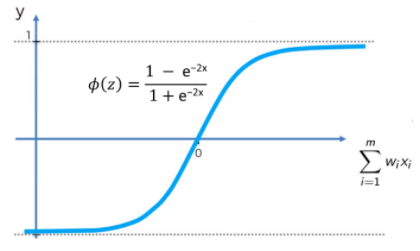
- Sigmoid의 중심을 0으로 맞추기 위해 개선된 함수, (-1,1), zigzag 현상이 덜하지만 값이 커지거나 작아지면 vanishing gradient 여전히 존재, Exp 연산 무거움 여전
ReLU (Rectified Linear Unit)
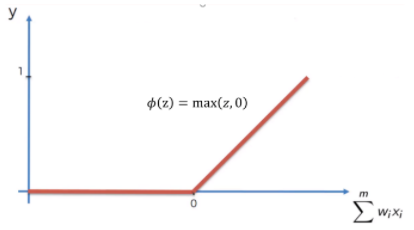
-
입력 값이 양수일 때에만 신호 전달, max(0,x)
-
계산 효율성 높음, Vanishing Gradient 문제 방지, Saturation 방지 (Sigmoid에서 값이 극으로 갈 수록 0,1로 수렴하는 것을 막음), 희소 활성화 (음의 입력은 0을 출력하여 활성화를 적게 하는 것)를 통해 계산 비용이 줄고 과적합을 줄이는 데 도움됨
-
dying ReLU 문제 존재, 출력이 0보다 작아 활성화가 되지 않으면 역전파 때 학습이 되지 않는 것을 의미
-
dying ReLU가 장점이 될 수도 있다. Sparsity를 창출하기도 하기 때문에 오히려 좋을 수도 있다.
-
initialization 시 bias를 양의 값으로 초기화 시 dying ReLU 어느 정도 방지 가능, Learning Rate를 줄여서도 방지 가능, ELU, Leaky ReLU, PReLU 사용으로도 방지 가능
Sigmoid vs ReLU
-
Sigmoid는 (0,1)이기 때문에 확률을 나타내는 데 유용, 특정 클래스에 속할 확률로 해석 가능
-
ReLU는 무한 범위이기에 회귀 문제에 사용, Vanishing Gradient 문제가 없어 많이 쓰이는 것
