[AI_basic] Loss function, Gradient Descent

김훈래·2024년 4월 20일
AIstudy

AI_basic

목록 보기
3/7
post-thumbnail

Loss function

  • ML이란 Target과 Predict 간 오차를 최소화 하는 방향으로 모델의 parameter들을 조정하는 것

  • MSE, Binary Cross-entropy, Categorical Cross-entropy 등등

  • NLP에서 자주 사용되는 오차함수 위주로 선택 공부

Negative Log Likelihood Loss

P(D∣θ)=∏i=1ny^θ,iyi(1−y^θ,i)1−yiP(D|\theta)=\displaystyle\prod_{i=1}^n\hat{y}_{\theta,i}^{y_i}(1-\hat{y}_{\theta,i})^{1-y_i}

  • Binary Classification 예제의 식은 위와 같음

  • Likelihood: 우도, 정답 라벨에 대한 확률값의 비교, 예측의 정확도를 측정, 이 값이 커질수록 좋은 모델

    log  P(D∣θ)=∑i=1nyilog(y^θ,i)+(1−yi)log(1−y^θ,i)log \;P(D|\theta)=\displaystyle\sum_{i=1}^ny_ilog(\hat{y}_{\theta,i})+(1-y_i)log(1-\hat{y}_{\theta,i})

  • Log Likelihood: 우도에 로그 씌운 것, 곱연산이 합연산으로 바뀌어 연산 용이

  • Negative Log Likelihood: Gradient Descent 사용 할때에는 Loss 값이 작아지는 방향으로 설계해야하므로 마이너스 적용한 것

  • Binary의 경우에는 sigmoid를 이용하기 때문에 0~1 사이의 하나의 값을 계산, Multiclass의 경우 softmax를 사용하기 때문에 C 차원의 벡터 형태, 각 클래스에 속할 확률을 계산

logP(D∣θ)=∑i=1nlog(y^θ,i)yilogP(D|\theta)=\displaystyle\sum_{i=1}^nlog(\hat{y}_{\theta,i})^{y_i}
  • Multiclass일 경우의 Log Likelihood 수식, yiy_i는 제곱이 아니라 upper index, True label과 관련되는 확률만 사용한다는 뜻

  • 위 gif와 같이 해당 인덱스의 값만 사용하여 summation 수행

Cross-Entropy Loss

  • 예측 분포 p, 정답 분포 q가 주어졌을 때의 cross-entropy는 Hp(q)=−∑i=1nq(xi)log  q(xi)H_p(q)=-\displaystyle\sum_{i=1}^nq(x_i)log\;q(x_i)

  • NLL Loss 식과 유사, 둘 다 두 분포의 유사도를 측정하는 방법, Cross-entropy는 LogSoftmax + NLL

  • 주로 분류 문제에서 이산 확률 변수에 사용

Mean Squared Error

  • 1n∑i=1n(yi−y^i)2\frac{1}{n}\displaystyle\sum_{i=1}^n(y_i-\hat{y}_i)^2

  • 주로 회귀 문제에서 연속 확률 변수에 사용

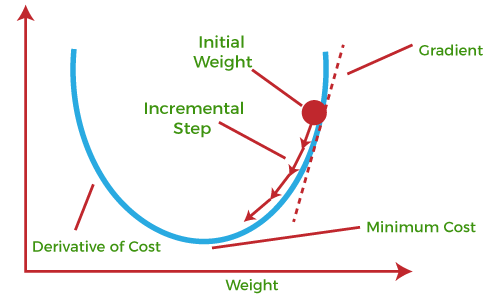
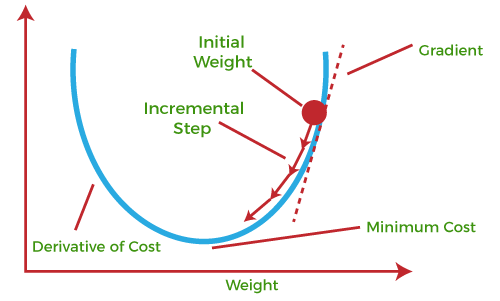
Gradient Descent

  • Optimizer 중 하나, optimizer는 GD -> SGD -> Adagrad, Momentum -> RMSProp -> Adam 등으로 발전되옴

  • w=w−α×δLδww=w-\alpha\times\frac{\delta L}{\delta w}

  • α\alpha는 learning rate, L은 loss

  • weight에 따른 loss function의 미분 계수의 방향으로 lr 만큼 weight를 갱신

  • b=b−α×δLδbb=b-\alpha\times\frac{\delta L}{\delta b}

  • bias도 같은 방식으로 조정

  • loss function을 그냥 미분해서 극소값을 찾으면 되지 않느냐?: loss function은 모델 구조 상 복잡할 수밖에 없음, 도함수를 계산하는 것이 불가능

L′(a)≈L(a+ϵ)−L(a−ϵ)2ϵL'(a)\approx \frac{L(a+\epsilon)-L(a-\epsilon)}{2\epsilon}
  • 따라서 위와 같이 미분할 때 미분계수의 정의를 이용하여 근사하는 방식을 채택
profile
김훈래
이전 포스트

[AI_basic] Activation function

다음 포스트

[AI_basic] Optimizer, Scheduler

0개의 댓글