이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.
링크: Khan academy

[진도율]

Vector intro for linear algebra

벡터 = 크기(magnitude) + 방향(direction)

• 5mph는 속력(speed)이며 scalar값이다.
• 방향까지 더해진 경우 속도(velocity)이며 vector값이다.

Real coordinate spaces

$R^2$은 2차원 유클리드 벡터공간이며 2-dimensional real coordinate space이다. 여기서 Real Number는 실수이고, R의 지수는 차원을 말한다. 즉, $R^2$은 2차원 공간상에 존재하는 모든 실수 벡터들의 집합이다. = all possible real-valued 2-tuple

마찬가지로, $R^3$은 3차원 벡터공간을 나타내며 3개의 실수 component (x, y, z)로 정의할 수 있는 모든 벡터들이 존재하는 공간이다. = all the real-valued 3-tuples in a 3-dimensional real coordinate space

• $R^2$에 속하는 (5,0)은 $R^3$에 속하지 않는다고 볼 수 있다.
• (i, 0, 1)에서 i는 real number가 아닌 imaginary number이므로 $R^3$에 속하지 않는다.

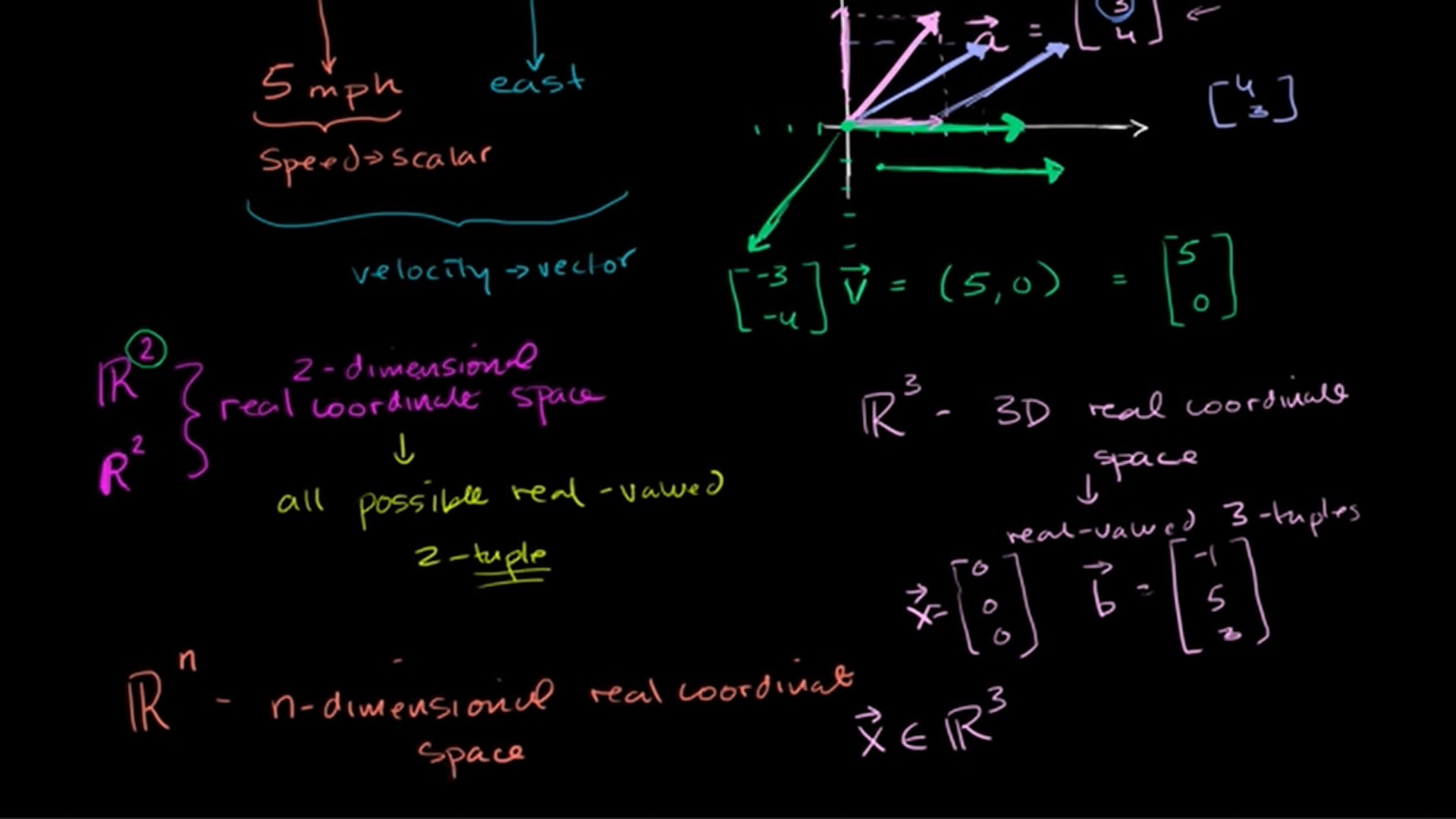$R^n$도 같은 맥락으로 n차원 실수 벡터로 이루어진 공간이라는 점 기억하시길.
= n-dimensional real coordinate space

Adding vectors algebraically & graphically

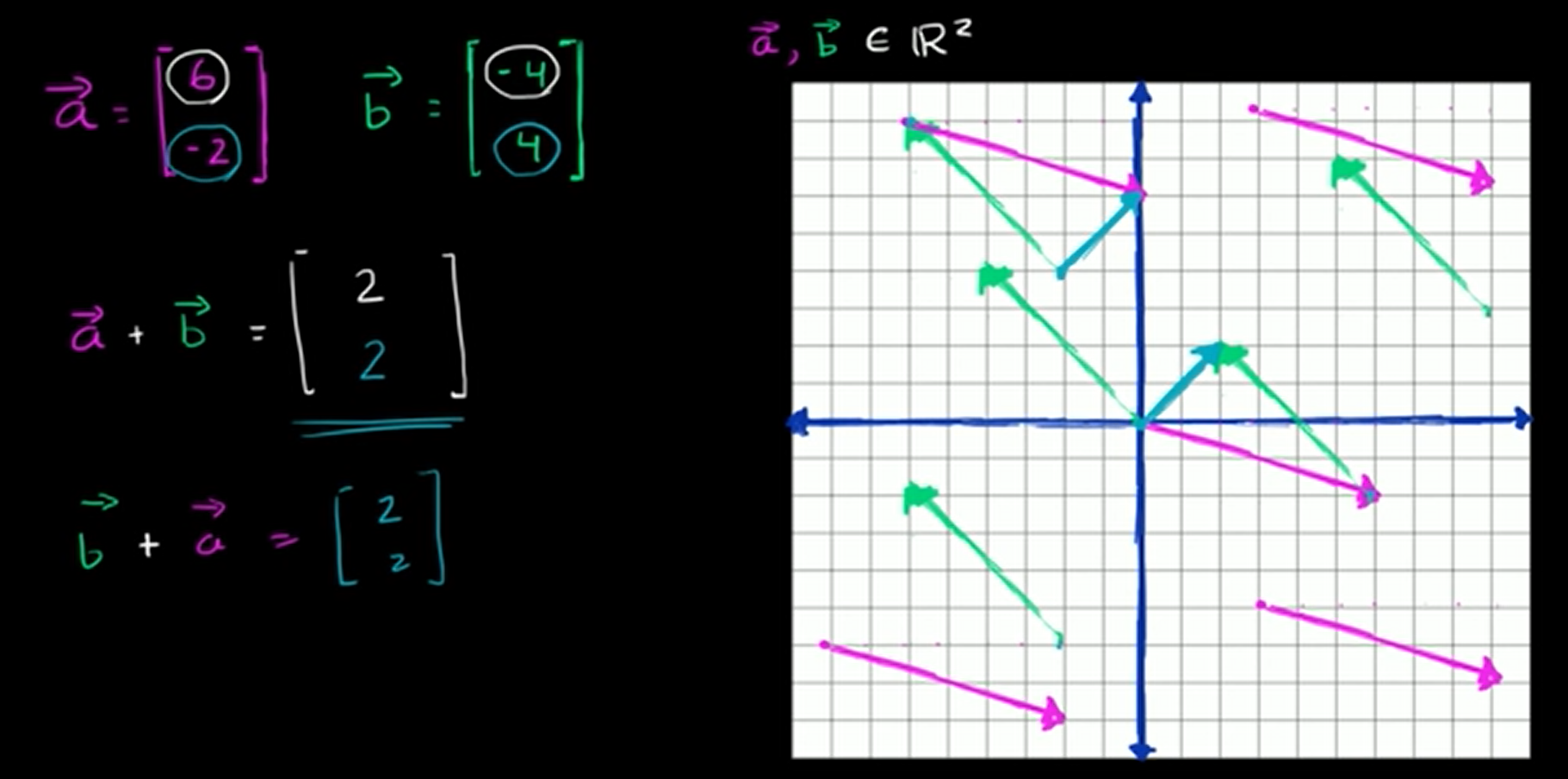
먼저, 벡터 연산 중 '더하기'다.

벡터의 합은 매우 직관적으로 할 수 있다. $\overrightarrow{A}$=(6, -2), $\overrightarrow{B}$=(-4, 4)인 경우를 예로 들어보자.

• $\overrightarrow{A}$ + $\overrightarrow{B}$ = $a_x$ + $b_x$ = (2, 2)
• $\overrightarrow{B}$ + $\overrightarrow{A}$ = $a_y$ + $b_y$ = (2, 2)

-> 즉, 순서에 상관없이 벡터 연산은 element-wise하게 이루어진다.

시작점이 꼭 origin (0, 0)일 필요는 없다.

어디에 있든지 같은 x축과 y축으로 동일하게 움직인다면 모두 같은 벡터이다.

그래프를 보자.

$\overrightarrow{A}$ + $\overrightarrow{B}$ 벡터 합을 vector A의 tail에서 시작하게끔 그린 후, vector B의 tail을 vector A의 head에서부터 시작하게끔 그리면 vector B와 vector A+B가 만나게 된다.

Multiplying a vector by a scalar

다음은, 벡터의 상수 배에 대한 내용이다.

벡터의 스칼라 곱은 양수와 음수일 때로 나눌 수 있다.

• 양수: 스칼라만큼의 크기 변화. 방향은 변하지 않음
  - Ex. 3a = (6, 3)
  
• 음수: 스칼라만큼의 크기 변화. 방향 반대로 바뀜.
  - Ex. -2a = (-2, -1)

Vector examples

벡터의 개념을 더욱 잘 이해하기 위해 벡터 연산부터 여러 예시들을 가져와 보았다.

위에서 다룬 내용의 복습이다.

벡터는 꼭 orgin (0, 0)에서 시작하지 않고, 만약 2차원 벡터라면 any point in $R^2$에서 시작하면 된다. ($x_1$, $x_2$)에서 시작한다고 가정할 때, a = (-1, 2)를 더해보자. 즉, ($x_1$-1, $x_2$+2)가 된다.

그래프를 보자.

vetor a, vector b 모두 2차원 벡터 공간 위에서 시작점이 다르기만 한다면 무한대로 그릴 수 있다. 이 벡터들은 모두 서로 평행이다. 그러나 관습적(convention)으로는 standard position인 (0, 0)을 시작점(initial point)로 잡는다.

vector a의 starting point에서 vector b의 end point로 가는 벡터를 그렸다고 해보자. 빨간선을 보면 결국 vector a와 vector b의 합이 된다.

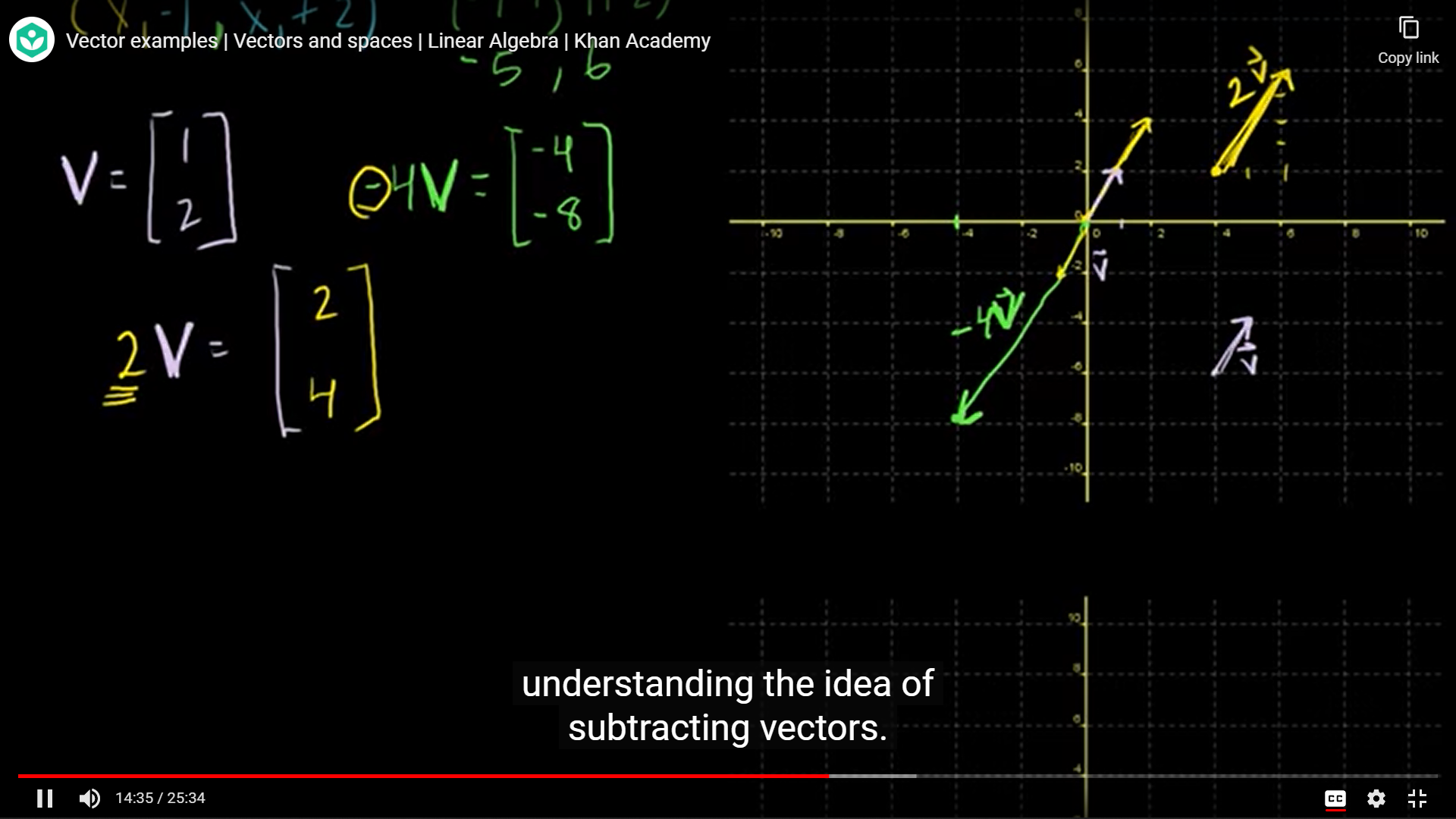
벡터를 Scale하면 어떻게 되는지 보자.

위에서 다룬 벡터 곱에 대한 내용으로, 양수값을 곱하는지 음수값을 곱하는지에 따라 방향이 달라진다는 점을 기억하면 된다.

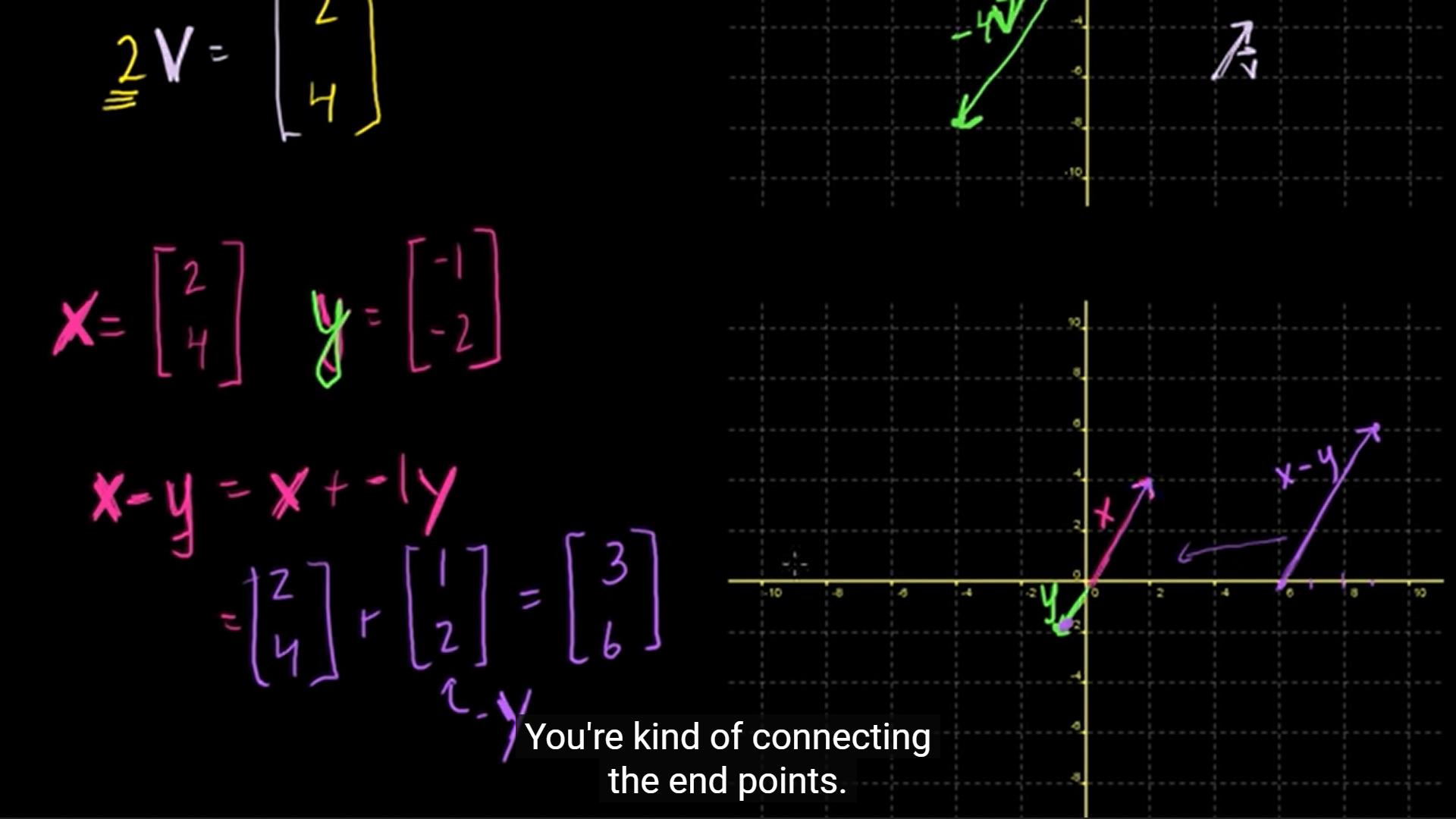
자연스럽게 벡터의 '뺄셈'에 대한 예시로 이어진다.

벡터의 차는 예시로 살펴보는 것이 한번에 이해하기 쉬울 것이다.

x = (2, 3), y = (-4, -2)일 때,
벡터의 뺄셈 x - y는 x + (-1y)와 같으므로,
-1 * y를 해준 벡터와 x와의 합으로 계산이 가능하다.

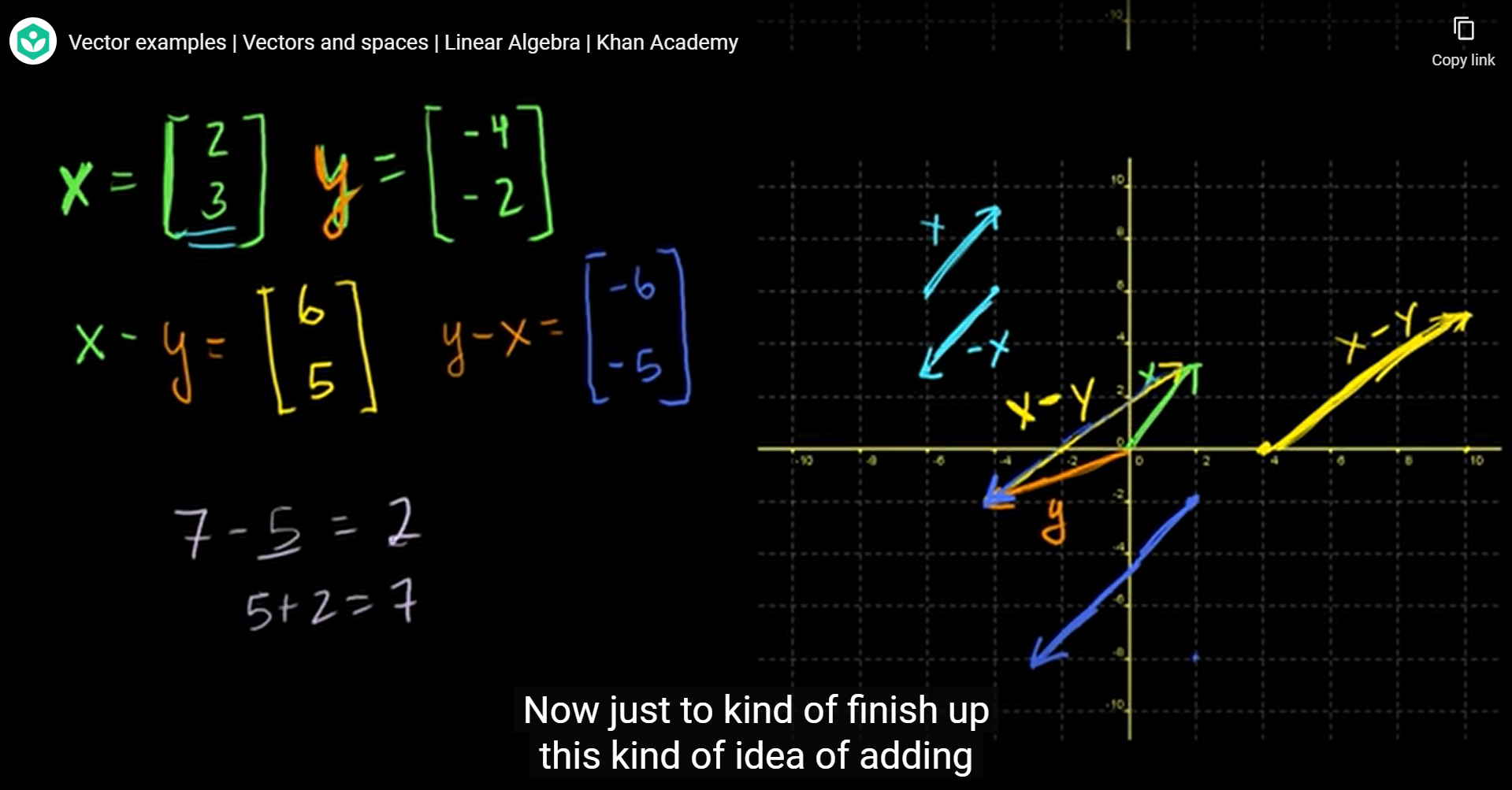벡터 사이의 차이(difference)는 결국 벡터의 차(vector x - y)가 된다.

직관적인 이해를 위해 기초적인 덧셈의 예시를 들자면,

• 7 - 5 = 2는 5 + 2 = 7이다.
• 이 식과 같은 맥락으로 벡터의 차를 이해하면 쉽다.

그래프 상으로 알 수 있는 벡터의 합과 차의 특징을 살펴보자면,

덧셈일 때는 첫번째 벡터의 tail(끝점)에서 두번째 벡터가 출발한다면
뺄셈일 때는 첫번째 벡터의 head(시작점)에서 출발한다.

일반화를 위해 4차원 벡터 $R^2$에서 연산을 해보겠다.

n 차원에서도 벡터 연산은 똑같이 적용된다.

4 * vector a - 2 * vector b의 연산을 하면 (-8, 0, 8, 2)라는 결과가 나온다. 즉, 4차원 공간을 그래프로 시각화하기에는 다소 어려움이 있지만, 이후에 다차원 공간(multi-dimensional)에서 벡터를 사용할 때 아주 유용한 개념이니 기억해두길 바란다.