이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.
링크: Khan academy

Unit vectors intro

Unit vector란?

: 단위 벡터, 길이가 1인 벡터이므로 각 차원의 수 만큼 존재한다.

Vector v를 $\overrightarrow{v}$ = (2, 3)라는 column vector로 표현할 수 있지만 $\overrightarrow{v}$ = 2$\overrightarrow{i}$ + 3$\overrightarrow{j}$와 같은 식으로도 표현이 가능하다.

• $\overrightarrow{i}$는 가로축의 unit vector
• $\overrightarrow{j}$는 세로축의 unit vector

🍁 3차원에서는 k의 개념까지도 나온다.

$\overrightarrow{b}$ = -1$\overrightarrow{i}$ + 4$\overrightarrow{j}$라고 할 때, $\overrightarrow{v}$ + $\overrightarrow{b}$는 무엇일까?

$\overrightarrow{v}$ + $\overrightarrow{b}$ = (2 + (-1))$\overrightarrow{i}$ + (3 + 4)$\overrightarrow{j}$ = $\overrightarrow{i}$ + 7$\overrightarrow{j}$이자 (1, 7) column vector로 표현할 수 있다.

Parametric representations of lines

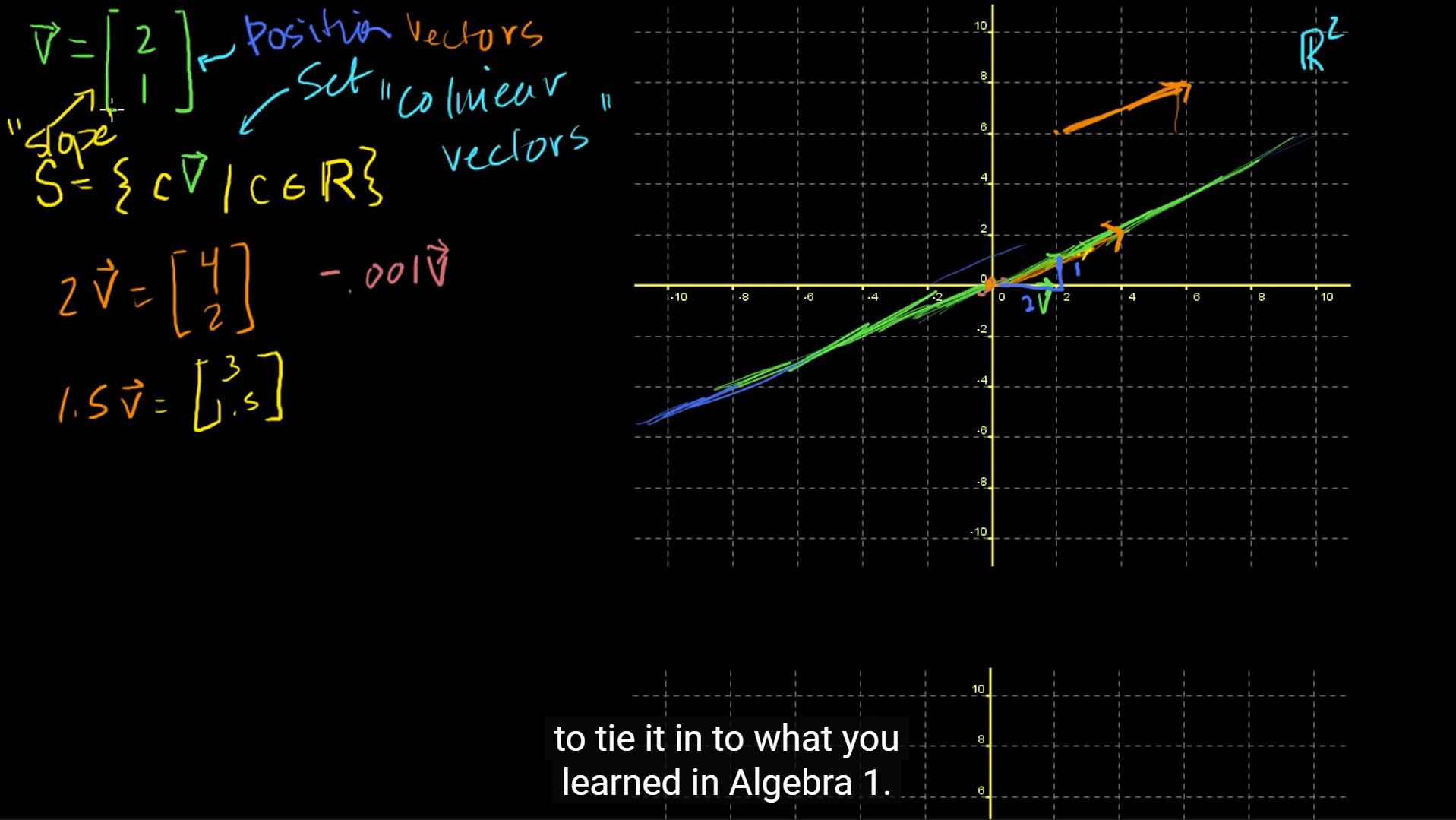$\overrightarrow{v}$=(2, 1)로 주어졌을 때, 좌표평면에 주황색 직선처럼 표현할 수 있다.
집합 S는 Vector v에 실수값(스칼라)을 곱한 집합을 나타내며, 초록색 직선과 같이 표현할 수 있다.

• Position vector: 좌표평면($R^2$) 어디에든 그릴 수 있지만 집합 S의 기준이 되는 벡터를 말한다.
• Collinear vector: Vector v에 스칼라 곱을 한 벡터. 여기서는 집합 S를 말한다.

🍁 사전적으로는 (점들이) 같은 직선에 놓여있다는 의미이다..

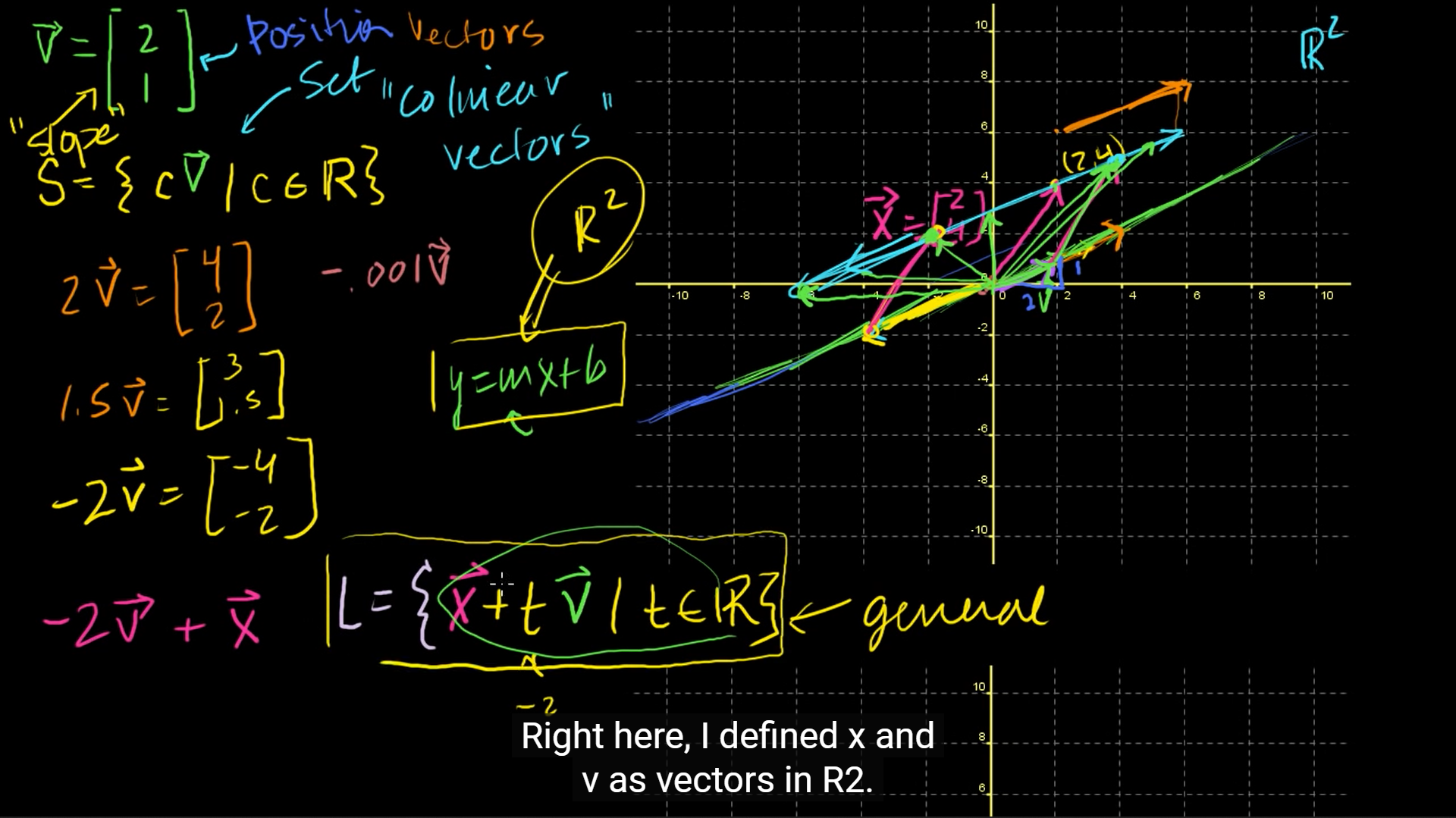$\overrightarrow{x}$ = (2, 1)일 때,
집합 L은 집합 S에 $\overrightarrow{x}$를 더한 것으로 집합 S와 평행한 기울기 $^1/_2$의 직선이 그려진다.
중학교 때 배웠던 $y = mx + b$로도 충분히 표현이 가능하지만,
L = { $\overrightarrow{x}$ + $t$$\overrightarrow{V}$ | $t \in R$ }로 표현하는 것이 더 좋다.

🍁 이런 표현식은 2차원 뿐만 아니라 더 많은 차원에서도 적용이 되는 "general"한 표현이기 때문이다.

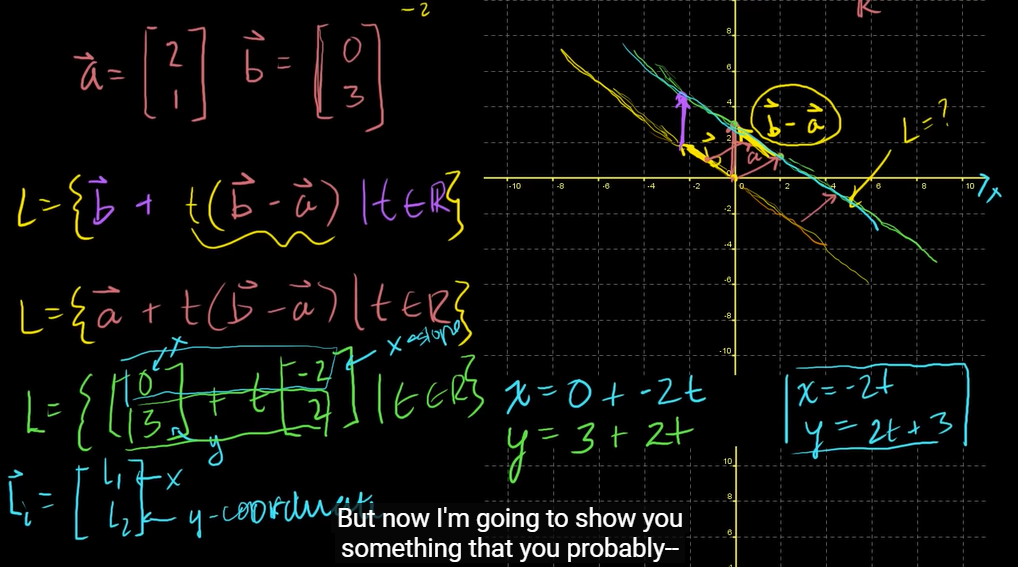$\overrightarrow{a}$와 $\overrightarrow{b}$ 지나는 직선을 L이라고 하자.
물론 중학교 때 기울기를 구했던 방식으로 해서 L 직선의 방정식을 구할 수는 있으나, 그 대신에 $\overrightarrow{b}$ - $\overrightarrow{a}$로 나타내 보고자 한다.

🍁 즉, vector a가 vector b로 가기 위해선 vector b - vector a를 하면 된다.

origin(0, 0)을 시작점으로 하는 $\overrightarrow{b}$ - $\overrightarrow{a}$의 standard form에서 좌표에 나와있는 집합 또는 직선 L로 바꿔주기 위한 식은,

• L = {$\overrightarrow{b}$ + $t($$\overrightarrow{b}$-$\overrightarrow{a}$) | $t \in R$ }
• L = {$\overrightarrow{a}$ + $t($$\overrightarrow{b}$-$\overrightarrow{a}$) | $t \in R$ }

이렇게 두가지로 표현이 가능하다.

$L_i$ = ($L_1$, $L_2$)에서 각각 $L_1$이 x-coordinate(좌표), $L_2$가 y-coordinate이면, Line의 parametric form으로 아래와 같이 표현할 수 있다.

• x = 2t
• y = 2t + 3

🍁 Line의 parametric definition을 표현하는 방법을 배워보았다.

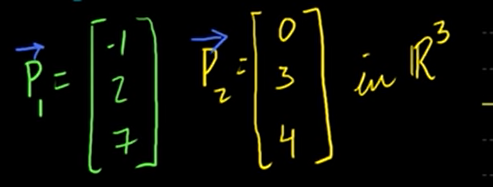3차원인 경우에 적용해보자.
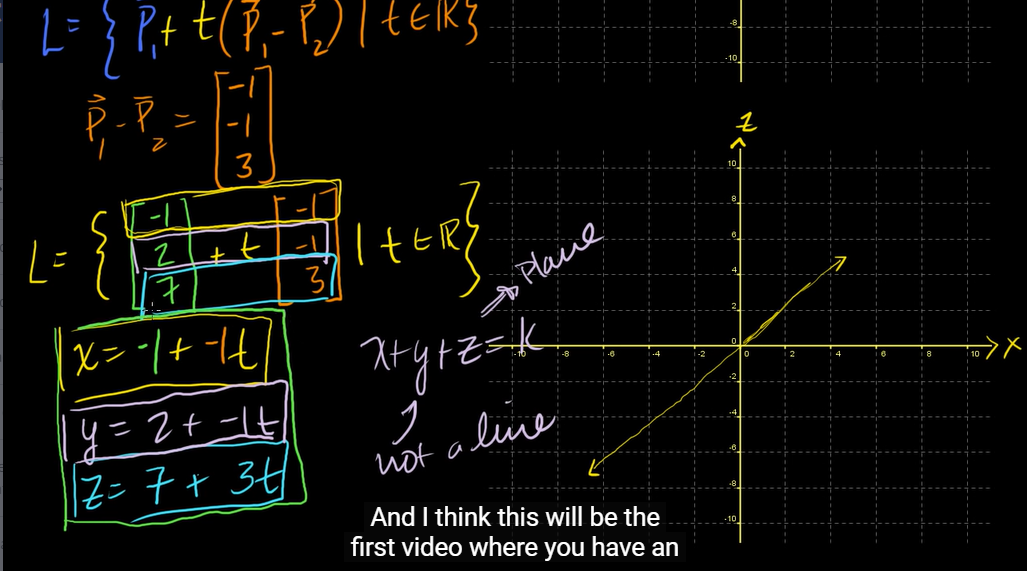3차원($R^3$)에서 Line의 parametric equation들을 아래와 같이 표현할 수 있다.
$x = -1 + -1t$
$y = 2 + -1t$
$z = 7 + 3t$

• 여기서 $t$(매개변수)는 arbitrary한 실수값이다.
• $x + y + z = k$는 직선이 아니며 plane(평면)일 뿐이다.

🍁 3차원에서 그치는 것이 아닌 50차원 100차원까지도 확장이 가능하다.

물론 시각화하기는 어렵겠지만 수학적으로 다루는 것에 있어서는 아무런 문제가 없다.