로지스틱 회귀분석: 특정 질병의 유무에 영향을 미치는 요인을 밝히는 통계 분석
-> 교란변수의 영향을 제거하고 여러 위험인자들이 관련되는 정도를 하나의 모형으로 설명 가능
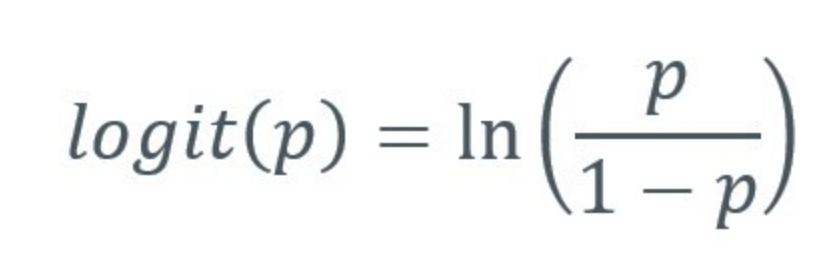Logit transformation을 통하여 < p는 각 수준에 따른 질병이 있을 확률,0<p<1 >
연속형 변수의 형태 가능
-로지스틱 회귀모형의 추정
최소제곱법 (Least Square Method)를 사용하는 선형회귀분석과는 달리 최대우도법 (Maximum Likelihood Method)를 이용해 회귀모형 추정!
모형에 필요한 변수를 결정하는 방법으로 우도비 검정 (Likelihood Ratio Test)을 이용
: 변수를 넣거나 빼면서 우도비 검정을 통해 변수들을 선택
우도법에 관한 설명 링크
https://velog.io/@hoyajhl/Biostatistics-%ED%86%B5%EA%B3%84-%EB%B6%84%EC%84%9D-likelihood%EC%9A%B0%EB%8F%84
Odds Ratio: exp(beta)-> 위험인자와 질병의 관련성을 보여줌(1보다 크면 요인에 의한 질병의 위험이 큰것으로 해석 가능)
*Odds Ratio 해석
오즈비의 공식을 통해 종속변수의 범주가 ‘1’이 감염이고 ‘0’은 정상인 이분형을 가정하면, P가 0.6이면, 오즈비는 (0.6/(1-0.6))=6/4가 되고 감염확률이 정상의 확률보다 1.5배 높다는 의미
Summary
회귀모형의 추정방법: 최대우도법 (Maximum Likelihood method)
회귀계수의 유의성: 우도비 검정 (Likelihood ratio test)
회귀모형의 평가: 분류표/ Nagelkerke의 R^2/Hosmer-Lemeshow 검정
Hosmer-Lemeshow의 Goodness of fit test 검정
-표본 수가 충분히 크다고 판단될 때 적용 가능, 아닌 경우엔 Nagelkerke의 R^2 이용
귀무 가설: 모형이 적합하다
대립 가설: 모형이 적합하지 않다
