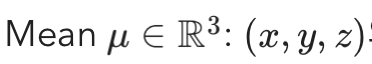0. 들어가기 전에
- input:
- 몇몇 각도에서 찍은 RGB 사진
- output
- 보고 싶은 카메라 view의 카메라 parameter만 정해주면, 그 view에서 보이는 RGB 이미지 도출 가능
- 알고리즘
- input을 이용하여, 3D 공간 상에 여러 gaussian distribution을 만듭니다.
- 각 gaussian distribution은 아래의 parameter들이 있고, 학습 과정에서 이 parameter들이 학습됩니다.
- mean
- covariance
- opacity (불투명도): 0~1
- color (색상): RGB
1. Introduction
- 3D reconstruction 분야에서 SOTA로 취급되던 NeRF보다 빠르면서도 좋은 성능
- 학습과정도 빠르고(3d 공간 상에 여러 gaussian distributions를 최적화)
- 6분
- 렌더링 과정도 빠르다. (만들어진 여러 gaussian distributions 로부터 특정 화각의 이미지로 rasterization 하는 과정)
- 100fps
- 학습과정도 빠르고(3d 공간 상에 여러 gaussian distributions를 최적화)
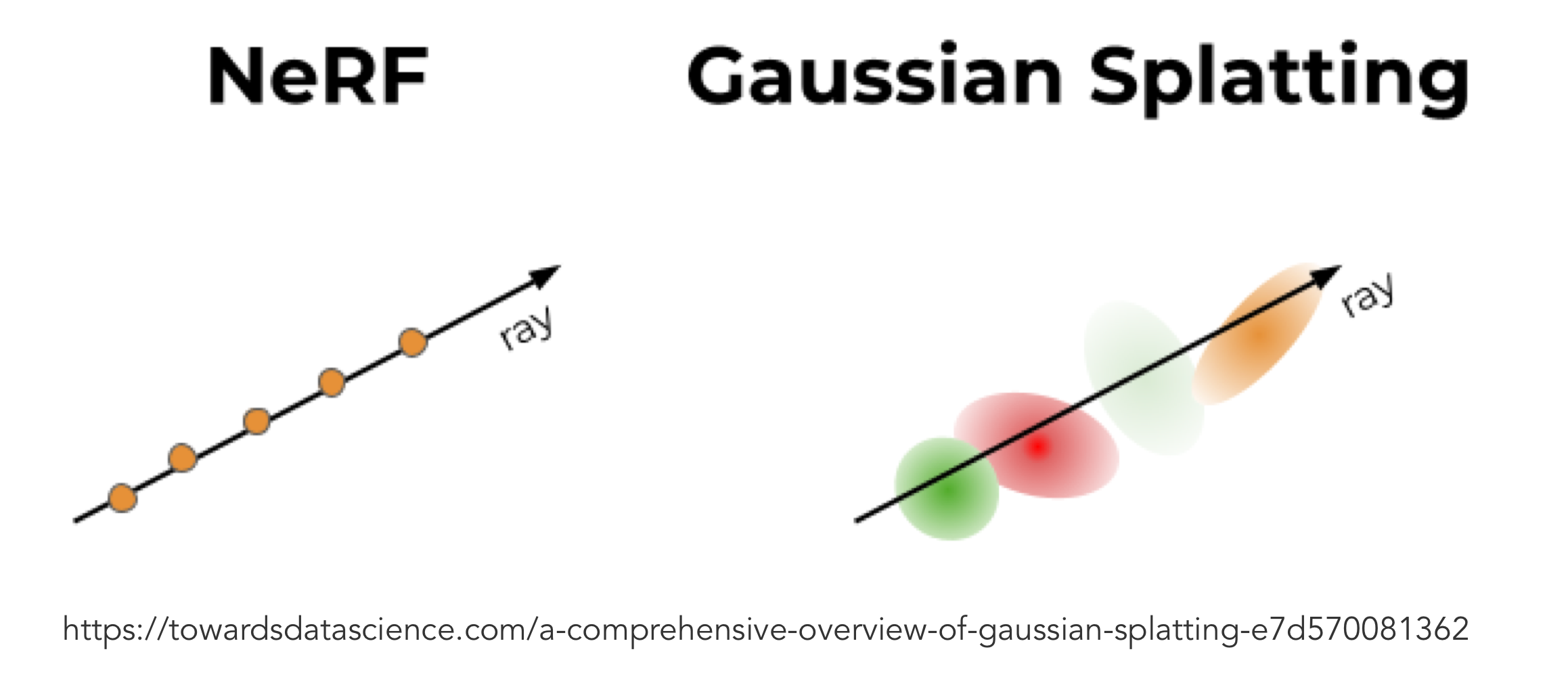
2. Nerf
- rendering 하는 법
- 이미지 각 pixel마다 각 ray를 그려서 여러 점을 샘플링하고,
- 샘플링한 각 점의 color와 volume density를 계산하고,
- ray위의 이 값들을 summation하여 이미지를 rendering 합니다.
- NeRF에서는
- input: (x,y,z) 좌표
- output: theta, phi 방향에서 봤을 때의
색과 density- density: 해당 지점에서 광선이 흡수되거나 산란되는 정도
- 밀도가 클수록, 빛 흡수와 산란 정도가 크다는 뜻
- -> 그 지점을 통과한 후, 광선의 감도가 감소
- 밀도가 클수록, 빛 흡수와 산란 정도가 크다는 뜻
- density: 해당 지점에서 광선이 흡수되거나 산란되는 정도
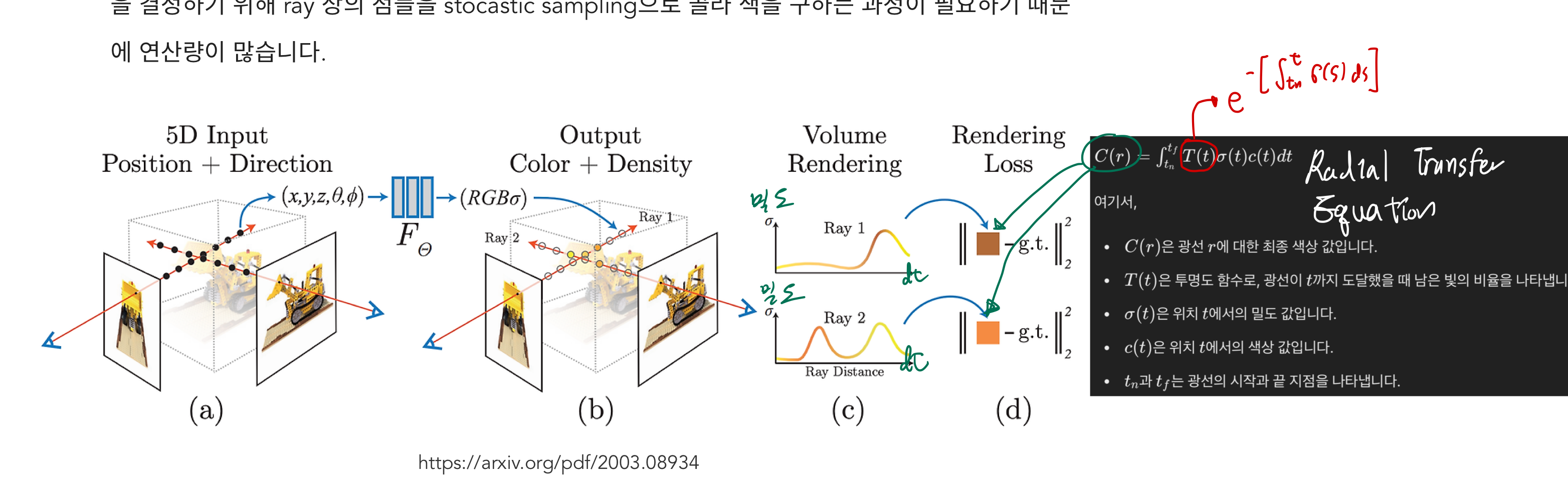
- 랜더링시 아래 이유로 연산량이 많음
- 특정 픽셀의 색을 결정하기 위해, ray 상의 점들을 stocastic sampling으로 골라 색을 구하는 과정이 필요하기 때문
- 아래 그림을 보면, 하나의 ray에 여러 pointcloud 들이 걸리고, (여기서 sampling이 필요)
- 이 샘플링된 point clouds를 기반으로 그 픽셀의 RGB 값을 정하는 로직이 필요
- 이 로직이 아래 그림의 Radial Transfer Equation
- 이 샘플링된 point clouds를 기반으로 그 픽셀의 RGB 값을 정하는 로직이 필요
3. 3D Scene Representatinos
3.1. meshes와 points를 이용하는 방법
- rasterization(3d -> 2d 이미지)에 GPU/CUDA 기반 최적화하기에 용이
- 가장 일반적으로 사용되는 방법
3.2. Gaussian Splatting 에서의 3D gaussian
- https://xoft.tistory.com/49
- 3D Gaussian으로 scene을 표현하는 방법 -> 이 논문에서 제안
- 각 guassian의
평균/분산/불투명도/(여러 각도에서 본)색상을 학습 시 최적화합니다.
mean
covariance (∑)
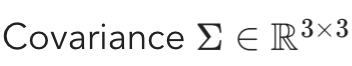
- anisotropic covariance matrix를 사용 -> Gaussian이 ellipsoid의 모양을 가질 수 있음
- TODO: 수학에 대해, 필요하면 정리 (GPT 아카이브에 저장해놨음)
- 각 방향축 에서 다른 분산 값을 가진다는 뜻
- 대각선이 아닌 행렬도 값을 가집니다.
- covariance matrix는 분산 값들이 0 이상의 정수이어야, 그 matrix가 covariance matrix의 의미를 담을 수 있습니다.
- 수학적으로는, Positive Semi Definite 해야
분산 값들이 0 이상의 정수를 가집니다.- 아래 정보는 Too Much
- Positive Semi Definite: 임의의 모든 non-zero vector v 에 대해,
vT∑v >= 0인 성질 - Positive Semi Definite 하면, ∑ 의 모든 eigenvalue 가 0 이상입니다.
- Positive Semi Definite: 임의의 모든 non-zero vector v 에 대해,
- 아래 정보는 Too Much
- 수학적으로는, Positive Semi Definite 해야
- 문제점:
- Gaussian Splatting에서 matrix (∑) 행렬의 원소 자체를 Gradient Descent로 최적화 하려다 보면,
Positive Semi Definite가 깨져버려서, 행렬이 음의 vairance를 가져버립니다.
- Gaussian Splatting에서 matrix (∑) 행렬의 원소 자체를 Gradient Descent로 최적화 하려다 보면,
- 해결책
- TODO: 이 부분 매우 중요한 trick인데, 완전히 이해는 못함. 필요하면 제대로 공부하기?
- covariance matrix를 Singular Vector Decomposition을 통해 -> eigen decomposition 합니다.
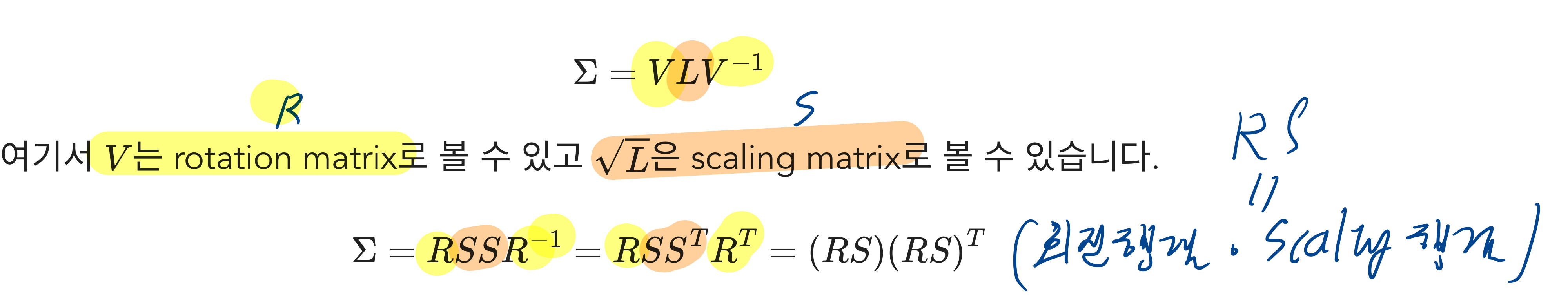
- 이렇게 표현된 covariance는 아래와 같이 해석 가능
- "unit covariance matrix를 가지는 데이터에 linear transformation 를 적용했을 때, 그 데이터의 covariance"
- 즉, rotation matrix와 scaling matrix를 위의 식대로 연산하여 구한 matrix는 covariance임이 보장됩니다.
- 그러므로, gradient descent로 rotation matrix의 quaternion (4 parameters)과 scaling matrix의 main diagonal (3 parameters)을 업데이트 함으로써 covariance matrix를 업데이트 할 수 있습니다.
R*S에 대해 Transpose값인ST*RT를 추가적으로 곱해 준 이유는, Covariance Matrix는 Symmetric한 성질을 갖기 때문에, 이러한 특성을 만들어주기 위함입니다
opacity (불투명도)
- Sigmoid가 적용되어 0(완전 투명) ~ 1(완전 불투명) 사이의 값을 가짐.
Color

- Gaussian이 하나의 RGB 값을 가지는 것이 아니라 view direction에 따라 다른 RGB 값을 가질 수 있도록
- view direction: polar angle (𝜃) + azimuthal angle (∅)
Spherical Harmonics coefficients를 이용해 표현- 어떤 물체의 색은 불변하지만 보는 방향에 따라 다르게 보이는 것을 모사
Spherical Harmonics(SH)란?- R, G, B 각각의 값을,
view direction에 따라 다르게 계산할 수 있게 한 수식 - R(𝜃, ∅) =
SH coeff R 1` * `Y_value_R_1` + ... + `SH coeff R N` * `Y_value_R_N - G(𝜃, ∅) =
SH coeff G 1` * `Y_value_G_1` + ... + `SH coeff G N` * `value_G_N - B(𝜃, ∅) =
SH coeff B 1` * `Y_value_B_1` + ... + `SH coeff B N` * `Y_value_B_N
- R, G, B 각각의 값을,
- 위 coeffients들을 최적화 하는 것이 학습 목표임
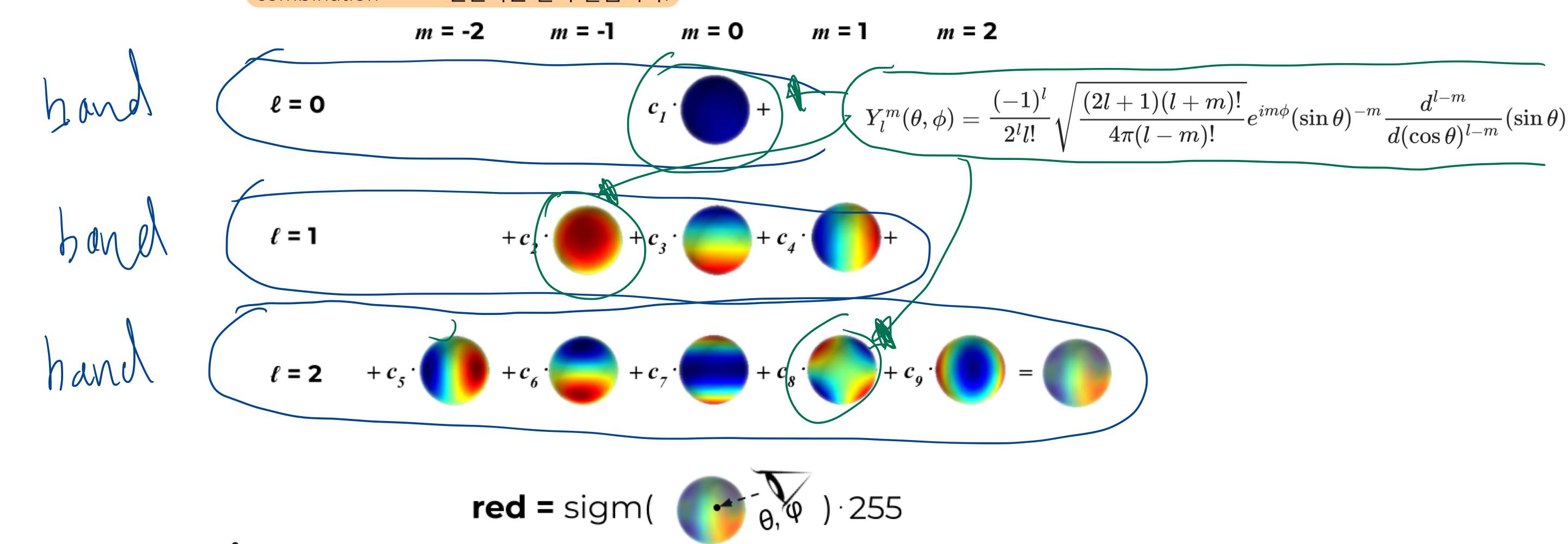

- 밴드 수 (l_max)를 정하면, SH 함수를 (l_max^2)개 쓰겠다고 하는게 확정됩니다.
4. Gaussian Splatting
-
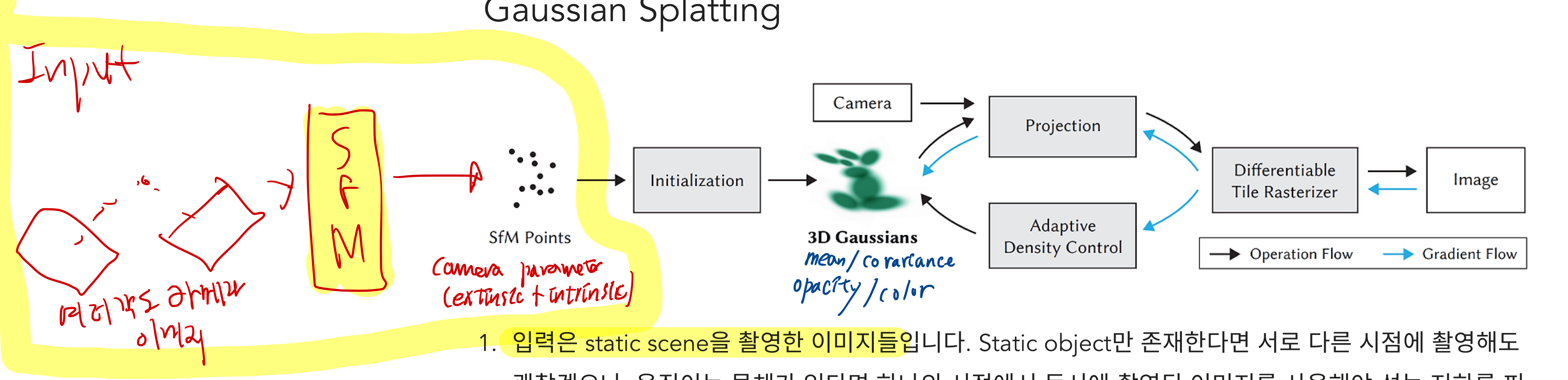
-
input
- 정적인 환경의 경우: 서로 다른 시간대에 촬영한 이미지들을 한꺼번에 input으로 넣어도 됨
- 동적인 환경의 경우: 서로 같은 시간대에 촬영한 이미지들을 한꺼번에 input으로 넣어야 함
-
TODO: SfM에 대해 정리한 글 링크 걸기 (예: COLMAP)
-
SfM으로 생성한 pointcloud 갯수만큼 -> gaussian distribution을 만들고, 각 위치를 이 distribution의 평균 값으로 초기화합니다.
-
Projection
- 3D Gaussian ->
(Camera에서 z축으로 거리가 1만큼 떨어진) Image Plane으로 Projection되어 2d gaussian 형태가 됩니다. 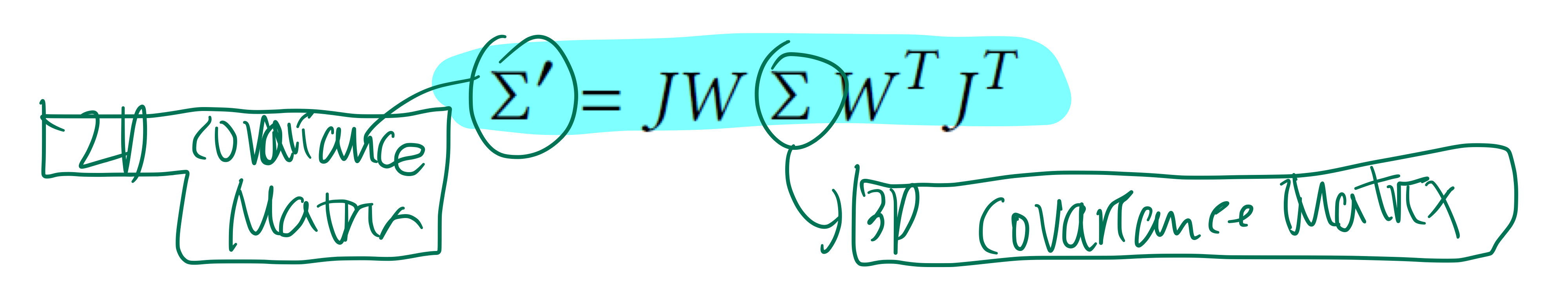
- 3D Gaussian ->
-
학습 (각 가우시안의 mean/covariance/opacity/color 의 최적화) 시키는 방법
- 특정 화각을 정해서, 3d 공간상의 여러 gaussian들을 rasterization 합니다.
Tile rasterizer을 사용했는데, 위 Image Plane 위의 2D Guassian들을 이용합니다.- https://xoft.tistory.com/52
- 알고리즘 (미분가능)
- 이미지를 14 by 14 pixels로 구성된 Tile들로 나누고
- Tile마다 Gaussian들을 depth로 정렬하고(visibility ordering),
- 앞에서부터 순차적으로 Alpha blending을 수행
- 그 과정에서 GPU sorting algorithm을 이용
알파 블렌딩- 픽셀의 투명도를 처리하는 기술
- 각 픽셀 색상과 불투명도(알파, 0~1) 값을 사용하여 최종 색상 계산
- 학습을 위해서는, 특정 화각에서 본 Ground Truth RGB 이미지가 있어야 함.
- gaussian splatting은 weight를 학습시키는게 아니므로, 새로운 scene에서 돌릴 때마다, 학습을 다시 시켜줘야 함
- 그러므로, 학습 시, gaussian splatting의 input으로 사용한 images를 Ground Truth data로 이용할 것으로 보임
- 2D projection 과정과, tile Rasterization 과정 모두 미분가능
- 정답 이미지로부터 Gaussians를 최적화 할 수 있음
- Gradient descent 이용: GPU를 최대로 활용하기 위해 -> 일부 operations에 custom CUDA kernels를 사용
- 특정 화각을 정해서, 3d 공간상의 여러 gaussian들을 rasterization 합니다.
-
-
하지만, 위 학습 과정만으로는, 최적 성능에 도달하는데에 한계가 존재하는데, 이유는 아래와 같음
- Gaussian distribution의
평균/분산/불투명도/(여러 각도에서 본)색상만 최적화 할 수 있지, - 분포의 갯수는 변경할 수 없음
- Gaussian distribution의
-
이를 극복하기 위해
- 100 학습 iterations 마다 Guassian의 수를 늘리거나 줄이는
Adaptive Density Control을 사용
- 100 학습 iterations 마다 Guassian의 수를 늘리거나 줄이는
5. Adaptive Density Control
- Optimization으로 Gaussians의 모양, 위치, 색을 바꿀 순 있지만 개수까지 바꿀 순 없습니다.
- 어떤 Gaussian이 너무 넓은 영역을 커버하거나 (over-reconstruction), 하나의 Gaussian으로는 표현하기 힘들어 보인다면 (under-reconstruction) 더 많은 개수의 Gaussian으로 표현할 필요가 있습니다.
- 100 iterations마다 Adaptive Density Control을 통해 under-reconstruction이나 over-reconstruction이 발생한 Gaussian을 둘로 쪼개게 됩니다.
- Under-/Over-reconstruction을 판단하는 좋은 기준은 view-space positional gradient가 크게 발생했는지 여부
- positional gradient
- view-space: 카메라 또는 관찰자의 시점을 기준으로 한 좌표계
- 3D 공간의 위치 변화(각 distribution의 mean 변화)에 따른
색상 변화와투명도 변화
- positional gradient
- 큰 view-space positional gradient가 발생했으면서 Gaussian의 크기가 작다면 under-reconstruction이, (clone 수행)
- 전체 volume 2배 증가
- Gaussian의 갯수 증가
- 큰 view-space positional gradient가 발생했으면서 Gaussian의 크기가 크다면 over-reconstruction (split 수행)
- 원본과 복사한 Gaussian 둘 다 1.6배 축소시킴으로써 전체 volume을 유지
- Gaussian의 갯수가 증가
- 문제점
- 카메라의 가까운 영역에 floater(떠 있는 것처럼 보이는) 이 생김. Gaussian이 무작위로 증가하는 형태로 나타남
- 두 경우 모두 똑같은 Gaussian을 복사해 positional gradient만큼 이동시키는데요,
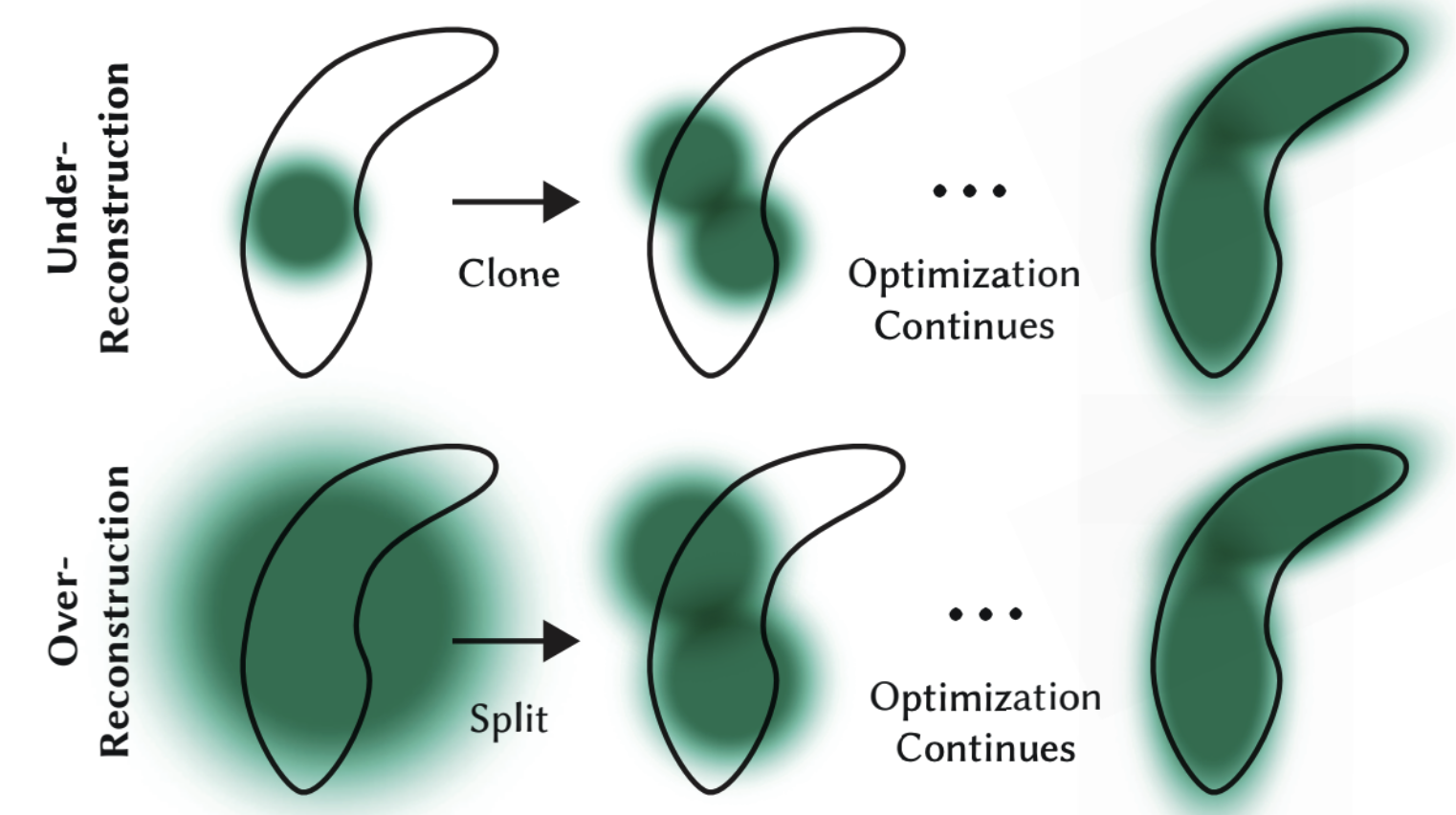
- Opacity 가 너무 작은 Gaussian은 삭제할 필요도 있습니다.
- 따라서 100 iterations마다 알파(불투명도)가 0.005보다 작은 Gaussian은 삭제해 줍니다.
- 3000 iterations마다 알파(불투명도)를 0에 가까운 값으로 초기화해 줍니다.
- 목적
- 뿌옇게 보이는 구름이 둥둥 떠다니는 것처럼 보이는 floater 현상을 줄이기 위해(위 split의 문제점),
- 3D Gaussian들이 중첩되는 경우도 발생 될 수 있는데, 주기적으로 alpha 값이 0으로 초기화 되면서 큰 크기의 Gaussian들이 중첩되는 케이스를 제거해줌
- 방식
- 0으로 초기화 한 후에는
- M,S,C,A를 Optimization하는 단계에서 100iteration동안 alpha값은 0이 아닌 값으로 바뀌게 되며,
- 100 iteration후에
Remove Gaussian연산(0.005 이하 불투명도)을 통해 원치 않는 값들이 제거
- 목적
6. Optimization
- Stochastic Gradient Descent (SGD)를 사용 -> 표준 GPU 가속 프레임워크를 이용할 수 있게 됨
- 일부 operation에 custom CUDA kernels를 적용
- Gaussian Splatting에는 neural network가 없습니다.
- 최적화의 대상은 Gaussians의 파라미터들 (mean, covariance, opacity, and color)입니다.
- 따라서 새로운 입력이 들어올 때마다 최적화 단계를 거쳐야 합니다.

- D-SSIM (Differentiable Structural Similarity Index):
- D-SSIM은 이미지의 구조적 유사성을 측정하는 SSIM(Structural Similarity Index)를 미분 가능하게 변형한 것
- SSIM은 이미지 품질 평가에서 중요한 지표로, 밝기, 대비(표준편차), 구조(공분산)를 고려하여 두 이미지 간의 유사성을 평가
- 안정적인 최적화를 위한 테크닉
- M(=mean=xyz) 파라미터에 대해 Exponential Decay Scheduling을 적용
- warm-up (초기 학습을 더 안정적으로 이루기 위해)
- input 이미지 resolution을 원본보다 4배 작게 시작한 후,
- iteration 250, iteraton 500 에서 두 배씩 키웁니다.
- 가우시안 분포의 색깔을 표시하는 SH coefficients는 view-dependent color를 표현하기 때문에 angular information의 부족에 취약
- NeRF같이 hemisphere의 거의 모든 각도에서 촬영한 이미지를 사용하면 괜찮지만
- 그렇지 않은 경우 zero-order component부터 틀려먹을 가능성이 있습니다.
- 이를 완화하기 위해 zero-order component만 최적화하는데서 시작해서, 1000 iterations마다 band를 하나씩 늘려갑니다.
- band를 1부터 학습 시작한다는 뜻임 (서서히 band 수를 늘려감)
7. Why Faster than NeRF?
- Gaussians를 공유하는 pixels에 대해서는 한 번의 2D projection만 하면 됩니다.
- 인접한 pixels일수록 같은 Gaussians를 공유할 가능성이 큽니다.
- NeRF의 경우 width x height x #sample 만큼의 MLP 연산이 필요하지만,
- Gaussian Splatting에서는 Gaussian이 그대로 사용됩니다.
- 따라서 ray sampling strategy를 고를 필요도 없습니다.
- NeRF에는 필요 없는 sorting 과정이 Gaussian Splatting에서는 필요하지만,
- frame당 한 번, GPU에서, differentiable custom CUDA kernels을 이용해 실행되기 때문에 빠름
- TODO: 이 부분 이해 안됨.
8. Limitations
- Gaussian Splatting도 NeRF와 비슷한 문제를 가지고 있습니다.
많은 뷰에서 커버하지 못한 부분의 퀄리티는 떨어지구요, floater 현상도 여전히 있습니다.- 심지어 GPU memory는 NeRF보다 몇 배는 더 필요합니다.
- 간단한 visibility 알고리즘을 사용하기 때문에 Gaussians의 순서가 갑자기 바뀌는 부분이 존재할 수 있음
- TODO: 어떤 visibility 알고리즘을 사용할까?
- Heuristic technique이 많이 사용됩니다. 실험적으로 정해진 값들이 많고, 안정적인 최적화를 위해 iterations마다 해줘야 할 일들이 있습니다.