1. 카메라의 원리
- 쉽게 이해하고 싶으면: https://www.youtube.com/watch?v=3fjLRebuxBg
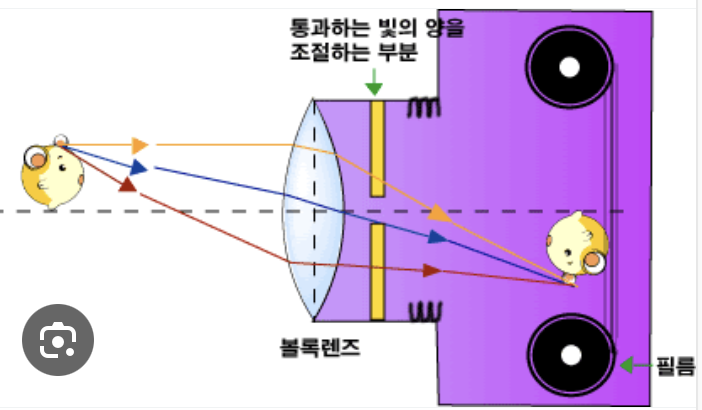
- 위 그림은 피사체에 초점을 잘 맞춰서, 피사체의 한 점이, 이미지센서(필름)의 정확히 한 점에 모이는 경우이다.
- 초점을 잘 맞춘다?: (카메라 렌즈와 이미지 센서간 거리를 잘 맞춰야 한다.)
- 카메라 앞부분을 돌리는 행위, 혹은 휴대폰 카메라의 0.5x, 1x, 1.5x 를 조정하는 것은
- 필름(이미지센서)의 위치를 조정하는 것이라고 이해하면 된다.
- 볼록렌즈
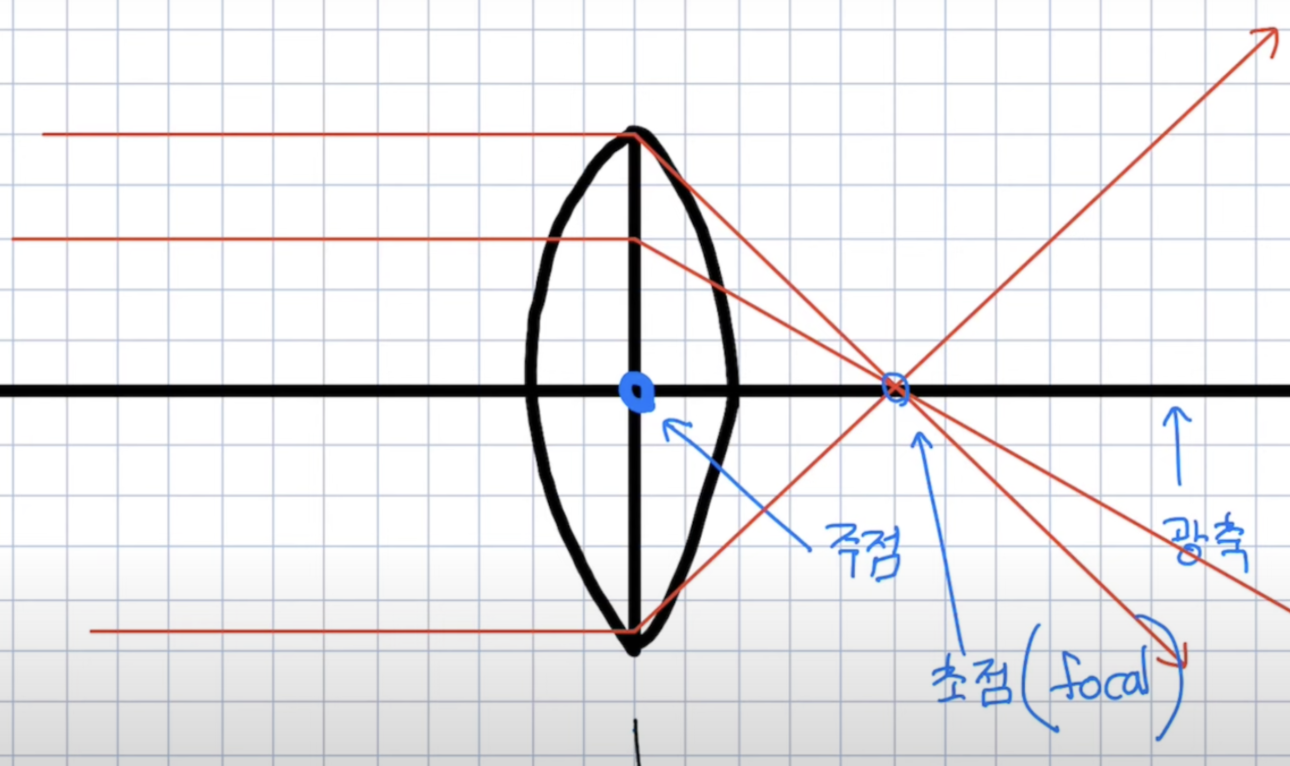
- 평행하게 빛이 들어가면, 초점으로 모이는 성질
- 주점으로 빛이 들어가면, 굴절되지 않는 성질
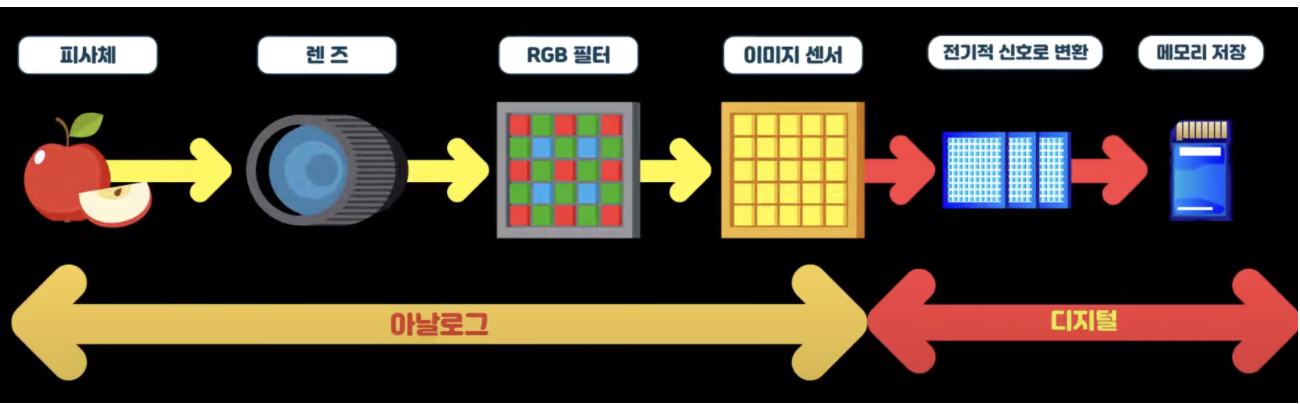
- 현대의 카메라는 디지털 방식으로, 아래와 같다.
- n만 화소: 이미지 센서에 배열된 화소의 개수가 n개이다.
2. intrinsic parameter 이란?
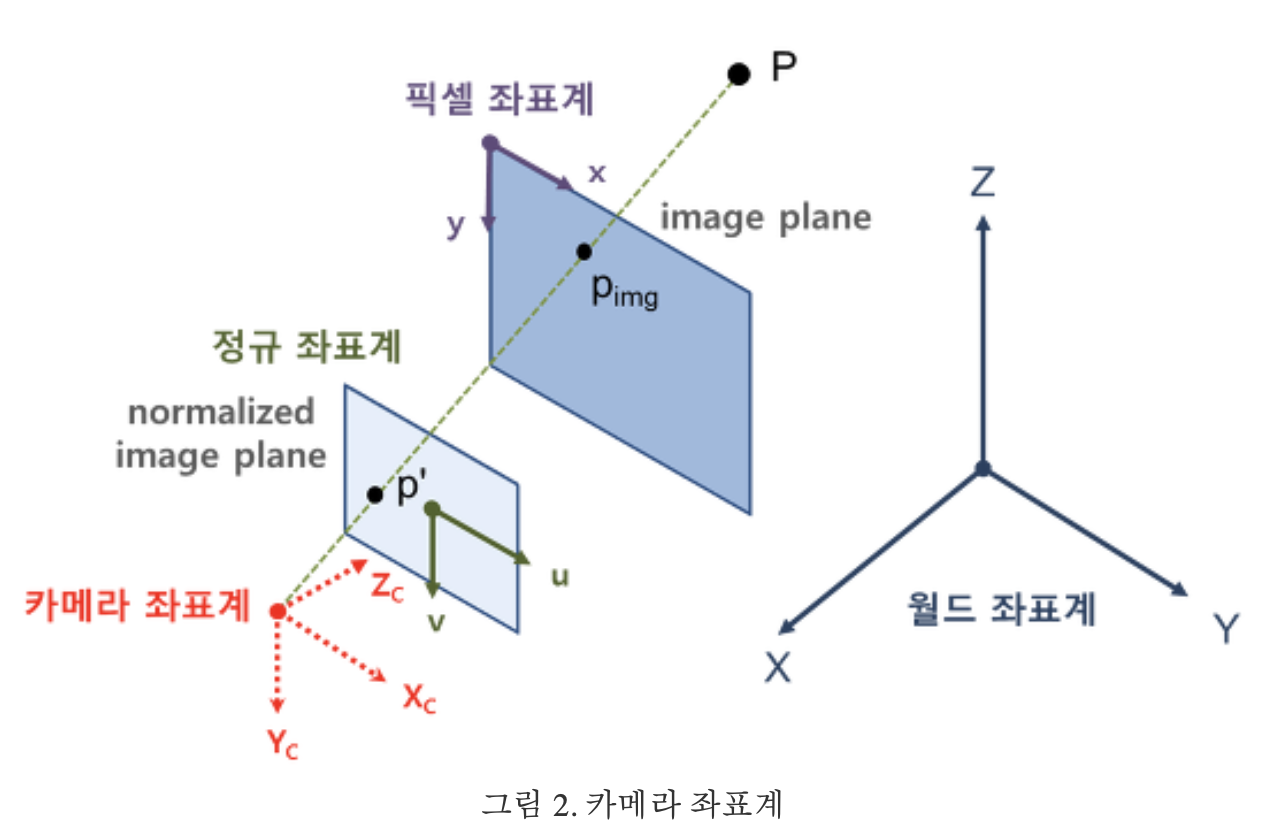
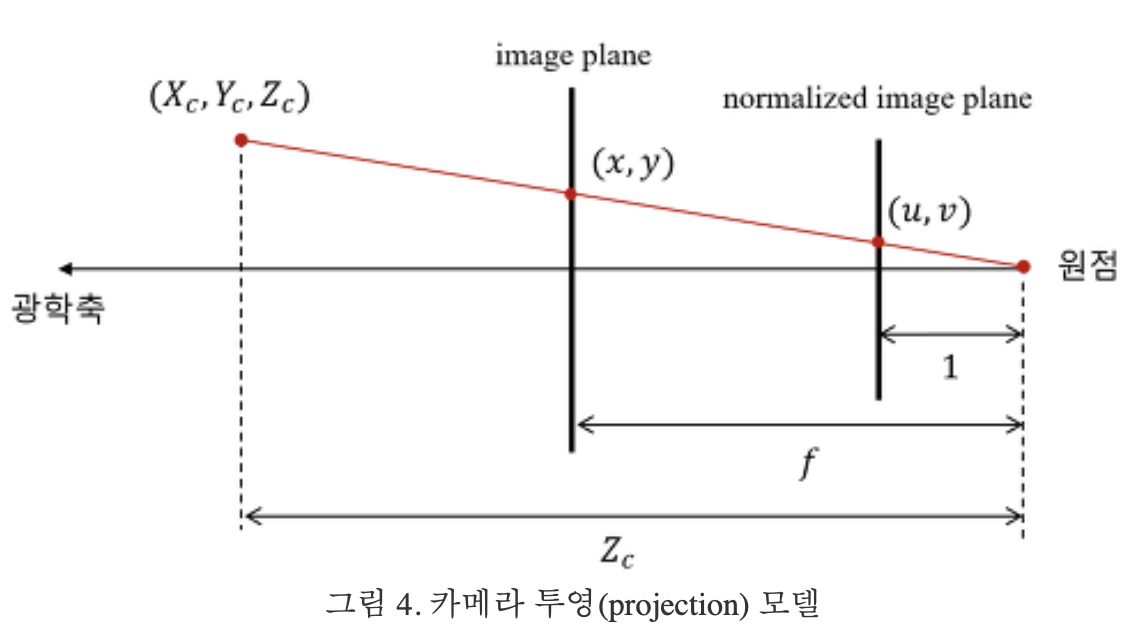
- 여기서 말하는 초점거리는,
주점과이미지센서간 거리를 의미하는 듯하다. 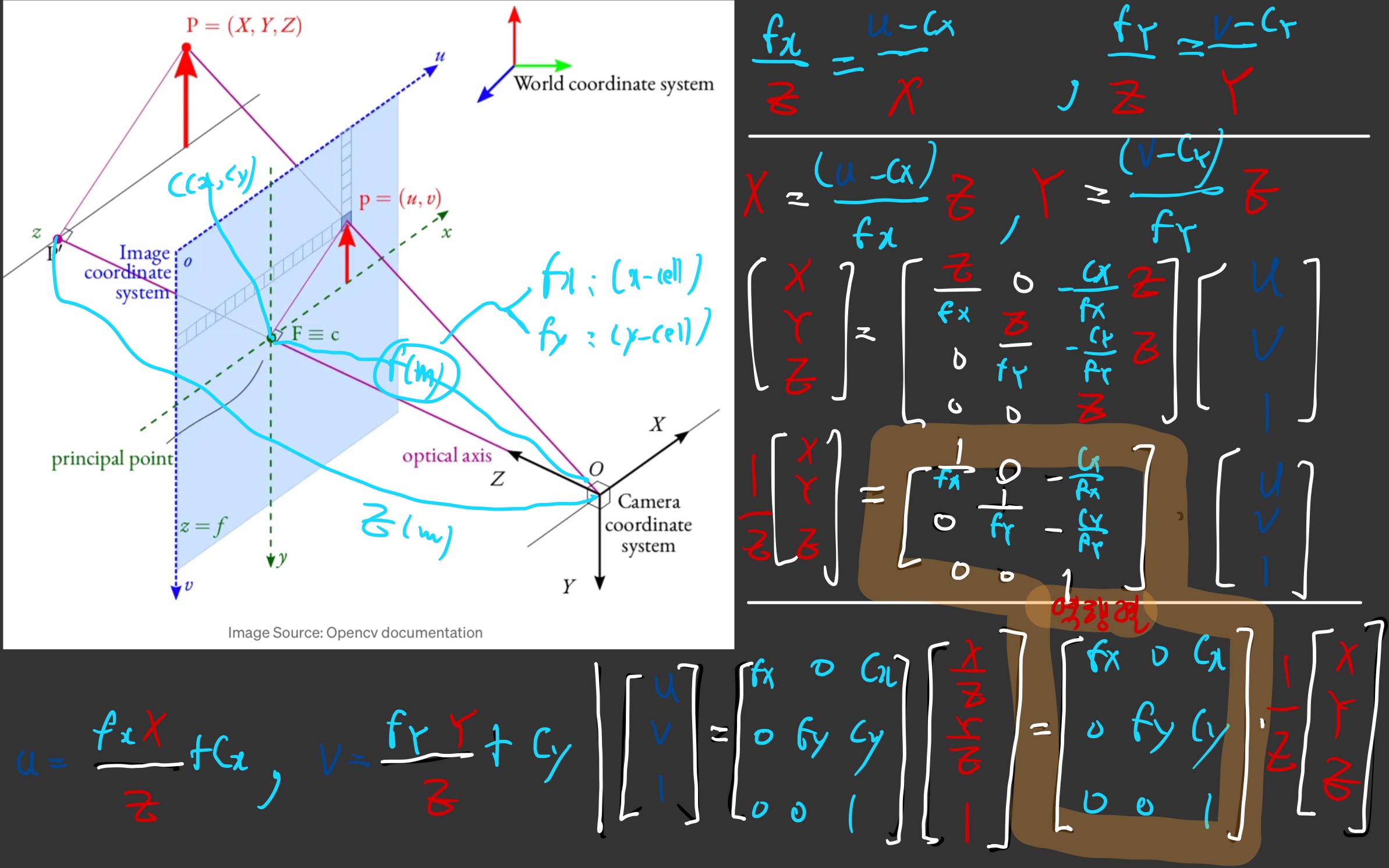
- 위 그림의 빨간색 (카메라 주점을 원점으로 하는 3D 절대좌표계의 좌표값) (X,Y,Z)를
- Z로 나누면, (X/Z, Y/Z, 1)이 되고,
- 이 값은
카메라 unit image plane에 매칭됨 카메라 unit image plane이란,카메라 주점과의 거리가 1인 image 평면을 의미
- (X/Z, Y/Z, 1) (
카메라 unit image plane)과,카메라 image plane간의 관계를 수학적으로 나타낸 것이intrinsic matrix - 다른 말로 하면, 공간의 한 점을
(빨간색) 카메라 주점을 원점으로 하는 3D 절대좌표계의 좌표값표현에서 ->image plane 좌표계로 변환하기 위한 matrix!
3. Camera Distortion?
- intrinsic parameter만 알면,
(빨간색) 카메라 주점을 원점으로 하는 3D 절대좌표계의 좌표값표현에서 ->image plane 좌표계로 변환이 될까?- 정답: 부정확하다.
- 이유:
- 위
카메라의 원리 1에서 말한 것처럼, 볼록렌즈의 문제로 인해, - 피사체의 특정한 한 점에서 나온 빛들이, 이미지 센서의 한 점으로 정확하게 모이지 않는다.
- 정확하게 모이려면, 초점을 잘 맞춰야 한다.(카메라 렌즈와 이미지 센서간 거리를 잘 맞춰야 한다.)
- 위
- 즉, 피사체의 각 부분(점)에서 방출된 빛이, 이미지 센서의 한 픽셀에 모이지 않는다. (여러 픽셀들에 투사된다.)
- 이것이 Distortion의 기본 원리이다. (비약 + 생략이 많음)
- (비약 + 생략이 많음)이러한 이유로, 단순히 intrinsic matrix(삼각비 공식)을 이용해서, 행렬 곱을 수행한다고,
(빨간색) 카메라 주점을 원점으로 하는 3D 절대좌표계의 좌표값표현에서 ->image plane 좌표계로 변환이 정확히 되지 않는다.
- distortion의 종료는 크게 2가지가 있다.
- https://velog.io/@hsbc/카메라의-왜곡
4. Extrinsic이란?
5. Camera Calibration?
5.1. 개요
- 아래 2개 값을 최소화하도록, 파라미터를 최적화하는 것.
- 촬영해서 얻은 이미지 plane (H,W,3)
- 3D XYZ 좌표계로부터, extrinsic / distortion model / intrinsic을 이용하여 구한 이미지 plane (H,W,3)
- 최적화할 파라미터? (TODO: 이 부분 공부가 제대로 안됨)
- extrinsic / distortion model / intrinsic의 모든 Parameter
- 최적화 알고리즘?
- Levenberg-Marquardt 알고리즘 같은 비선형 최소 제곱법
5.2. 준비물
-
체스보드 패턴 판 (하얀 벽에 부착하라)
-
OpenCV 라이브러리 (python)
-
조명이 일정하고 움직임이 없는 환경
- 캘리브레이션 보드를 다양한 각도와 거리에서 촬영
5.3. opencv-python 사용
5.3.1. 체스보드의 각 특징점의 3D world 좌표계(객체 지점) 설정하기
- 각 이미지에서 보드의 전체 패턴이 포함되도록 촬영해야 함
- 이들 이미지는 여러 카메라로부터 촬영되었고,
- 체스 보드는 정적으로 고정된 위치에 있었지만,
- 각 카메라 촬영 관점에서, 체스 보드는 다른 위치와 방향에 놓여 있습니다.
- 체스판의 3D XYZ 좌표를 단순화시키기 위해,
- 체스판이 XY 평면을 유지하고 있는 절대좌표계를 도입(즉, 체스판 위의 모든 점의 Z=0이 되도록 좌표계를 도입)
- 그리고 카메라는 이에 따라 움직이고 있습니다.
- 이러한 중요한 가정이 오직 X, Y값만을 계산하는 것으로 단순화시켜 줍니다.
- 이제 X,Y 값에 대해, 지점의 위치를 나타내는 (0,0), (1,0), (2,0), … 형식으로 단순하게 전달할 수 있습니다.
- 이 경우, 결과는 체스판에서의 사각형의 크기 축척으로 구해집니다.
- 그러나 만약 이 사각형의 크기를 알고 있다면(30mm라고 말할 수 있다면), mm 단위 결과로써 (0,0), (30,0), (60,0), …처럼 전달할 수 있습니다.
- TODO: 코드에 넣을 때는, 그냥 (0,0), (1,0), (2,0), … 형식으로 단순하게 전달하는 것 같음
# 체스보드 패턴 생성
# 체스보드 크기
chessboard_size = (9, 6) # column 수, row 수
# objp: (9 * 6, 3)
objp = np.zeros((np.prod(chessboard_size), 3), np.float32)
"""
- np.mgrid:
- (2, column 수, row 수): (column 수, row 수)행렬이 2개인데,
- 각각 height 좌표, width 좌표를 의미
- (2, column 수, row 수).T = (row 수, column 수, 2)
- reshape: (column 수 * row 수, 2)
- 이 뜻은,
- ( column 수, row 수) array를,
- height 순으로 읽어내려가겟다는 뜻이다. (세로 줄 하나씩 위에서 아래로 읽어가겠다는 뜻)
- objp[:, 0]: height index
- objp[:, 1]: width index
"""
objp[:, :2] = np.mgrid[0:chessboard_size[0],
0:chessboard_size[1]].T.reshape(-1, 2)5.3.2. 2D 이미지 지점에서의 checkerboard 패턴 찾기
cv2.findChessboardCorners()이용- 이 함수는 코너 지점과 패턴이 발견되었는지의 여부를 반환
- 이들 코너 지점들은 위치상 왼쪽에서 오른쪽으로, 위에서 아래로 정렬되어 있습니다.
- 일단 코너를 발견하면, cv2.cornerSubPix() 함수를 사용하여 정확도를 높일 수 있습니다.
- 또한 cv2.drawChessboardCorners() 함수를 사용해 코너 결과를 그릴 수 있습니다.
- 각 코너를 원이나 점으로 표시
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
imgpoints = []
# 이미지 로드
images = ["IMG_3323.jpg"] # 캘리브레이션 이미지 파일 리스트
for image in images:
img = cv2.imread(image)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# corners: np.array (N, 1, 2)
ret, corners = cv2.findChessboardCorners(image=gray,
patternSize=chessboard_size,
corners=None)
if ret:
objpoints.append(objp)
# corners2: cv2.typing.MatLike # cv2.mat_wrapper.Mat, NumPyArrayNumeric
# corners2: np.array (N, 1, 2)
corners2 = cv2.cornerSubPix(image=gray,
corners=corners,
winSize=(11, 11),
zeroZone=(-1, -1),
criteria=criteria)
imgpoints.append(corners2)
# 코너를 이미지에 그립니다.
cv2.drawChessboardCorners(img,
patternSize=chessboard_size,
corners=corners,
patternWasFound=ret)
# 결과 이미지를 저장합니다.
output_image_path = f"output_{image}"
cv2.imwrite(output_image_path, img)- 메서드에 대한 자세한 사용법이 궁금하면: https://velog.io/@hsbc/카메라-intrinsic-정확히-구하기
5.3.2.1. cv2.drawChessboardCorners()
- 이 함수는 다양한 환경에서 감지 강건성을 높이기 위해, 보드 주변에 넓은 흰색 공간(테두리가 두꺼울수록 좋음)이 필요
- 그렇지 않으면 테두리가 없고 배경이 어두운 경우 외부 검은 정사각형을 제대로 분할할 수 없어서 정사각형 그룹화 및 순서 지정 알고리즘이 실패합니다.
- gen_pattern.py(캘리브레이션 패턴 생성)를 사용하여 체커보드를 생성하세요.
- https://github.com/opencv/opencv/blob/4.x/doc/pattern.png
5.3.2.2. cv2.cornerSubPix
- 이 함수는 코너 주변의 이미지 그레이디언트를 계산하여 코너 위치를 미세하게 조정
- 설정된 반복 횟수 또는 정확도 기준에 도달할 때까지 정제 과정을 반복
- winSize: 코너 주변을 고려할 윈도우 크기
- zeroZone:
- 중앙 영역의 크기를 설정하여 노이즈를 제거하는 데 사용.
- 일반적으로 (-1, -1)로 설정하여 모든 영역을 고려
5.3.3. intrinsic / extrinsic / distortion parameter 구하기
- 위 과정을 통해, 우리는 체커보드 특징점의 3D 좌표계(
objpoints)를 구했고, - 각 체커보드 특징점에 매칭되는 (N개 view)의 이미지 plane에서의 각 이미지 좌표들(
imgpoints)을 구했습니다. - 이제 우리는
cv2.calibrateCamera메서드를 이용해, intrinsic / extrinsic / distortion parameter을 구할 수 있습니다. - 이론적 이해? https://velog.io/@hsbc/camera-calibration-이론
(ret, mtx, dist, rvecs, tvecs) = cv2.calibrateCamera(objpoints,
imgpoints,
imageSize=gray.shape[::-1],
cameraMatrix=None,
distCoeffs=None)
"""
ret: float
- 전체 Root Mean Square re-projection error
- 이 값은 캘리브레이션 과정의 품질을 나타내며, 낮을수록 더 정확한 캘리브레이션 결과를 의미
- 0.4043353
mtx: np.ndarray (3, 3)
- intrinsic matrix
- [[2.82941040e+03 0.00000000e+00 1.97697417e+03]
[0.00000000e+00 2.82939480e+03 1.46900315e+03]
[0.00000000e+00 0.00000000e+00 1.00000000e+00]]
dist: np.ndarray (1, 5)
- `[k1, k2, p1, p2, k3]`을 포함하며,
- 이는 각각 반경 왜곡 계수(k1, k2, k3)와 접선 왜곡 계수(p1, p2)
[[ 0.09491546 -0.22681414 0.00043416 0.00034345 0.18057507]]
rvecs: Tuple[np.ndarray]
- (np.ndarray (3, 1), ...)
- 각 패턴 뷰에 대한 회전 벡터의 튜플.
- 각 뷰에 대한 3x1 회전 벡터로, 월드 좌표계를 카메라 좌표계로 변환하는 회전을 나타냅니다.
- 이 벡터는 Rodrigues 변환을 통해 회전 행렬로 변환할 수 있습니다.
- (array([[ 0.01413114],
[ 0.01593625],
[-0.00571477]]),)
tvecs: Tuple[np.ndarray]
- 설명: 각 패턴 뷰에 대한 변환 벡터의 튜플.
- 값의 의미:
- 각 뷰에 대한 3x1 변환 벡터로, 월드 좌표계를 카메라 좌표계로 변환하는 평행 이동을 나타냄
- `(array([[-3.89025738],
[-2.26881858],
[ 7.43518093]]),)`
"""- TODO: 아래 부분 공부 필요
cv2.calibrateCamera알고리즘은 다음 단계를 수행합니다:- 초기 내부 파라미터를 계산하거나 입력 파라미터에서 읽습니다.
- 왜곡 계수는 초기에는 모두 0으로 설정
- intrinsic 파라미터가 이미 알려진 것처럼 초기 카메라 포즈(extrinsic)를 추정
- 재투영 오차, (re-projection error)
- 즉
- 관찰된 특징점
imagePoints와 - 투영된 (현재 카메라 파라미터와 포즈를 사용한) 객체 점
objectPoints간의 - 거리 제곱합을 최소화하는 글로벌 Levenberg-Marquardt 최적화 알고리즘을 실행
- 관찰된 특징점
- 자세한 내용은
projectPoints를 참조하십시오.
5.3.4. intrinsic matrix 개선하기
cv2.getOptimalNewCameraMatrix()함수를 사용하여카메라 메트릭스(intrinsic)를 개선할 수 있음- intrinsic에 distortion을 반영!
- 새롭게 구해진 intrinsic matrix는,
촬영된 이미지 plane<->undistored된 normalized image plane간 변환을 가능하게함 - 13개의 샘플 이미지 중
왜곡 현상을 제거할 하나를 사용해 이미지의 크기를 얻고,카메라 메트릭스(intrinsic)를 얻는 코드는 다음과 같습니다.
# img = cv2.imread('./data/chess/left12.jpg')
h, w = img.shape[:2]
(newcameramtx, roi) = cv2.getOptimalNewCameraMatrix(cameraMatrix=mtx,
distCoeffs=dist,
imageSize=(w, h),
alpha=1,
newImgSize=(w, h))
"""
newcameramtx: np.ndarray (3, 3)
- `출력되는 새로운 카메라 intrinsic 행렬.`
- [[2.86704074e+03 0.00000000e+00 1.97858396e+03]
[0.00000000e+00 2.86554634e+03 1.47026838e+03]
[0.00000000e+00 0.00000000e+00 1.00000000e+00]]
roi: Tuple[int]
- 선택적 출력 사각형으로, `왜곡 보정된 이미지에서 모든 유효 픽셀 영역을 둘러싼 사각형`
- (x, y, w, h)
- ROI 영역
- (14, 12, 3997, 2995)
"""5.3.4.1. cv::getOptimalNewCameraMatrix 함수
- 자유 스케일링 파라미터(alpha)를 기반으로, 최적의 새로운 카메라 내부 행렬(intrinsic)을 반환
- alpha:
- 자유 스케일링 파라미터로, 0~1 사이
- 0
- 원본 이미지의 유효한 픽셀만, 보정된 이미지로 가져오기
- 원본 이미지의 원치않는 픽셀을 최소로 갖는 보정된 이미지가 얻어지는데,
- 원본 이미지의 코너 지점의 픽셀들이 제거될 수도 있음
- 왜곡 보정된 이미지의 모든 픽셀이 유효한 pixel임
- 1
- 원본 이미지의 모든 픽셀은, 보정된 이미지에 유지됩니다.
- (
원본 이미지의 모든 픽셀이왜곡 보정된 이미지에 유지)
- 알파가 0보다 클 때, 왜곡 보정된 결과는,
- 캡처된 왜곡 이미지 밖의 "가상" 픽셀에 해당하는 일부 검은 픽셀을 가질 가능성이 있습니다.
- TODO: 공부 필요
- 반환 값
- new_camera_matrix:
출력되는 새로운 카메라 intrinsic 행렬.- np.ndarray (3, 3)
- validPixROI:
- 선택적 출력 사각형으로,
왜곡 보정된 이미지에서 모든 유효 픽셀 영역을 둘러싼 사각형 - Tuple[int]
- (x, y, w, h)
- (14, 12, 3997, 2995)
- 선택적 출력 사각형으로,
- new_camera_matrix:
5.3.5. 왜곡 제거하기
- 이제
- extrinsic matrix도 구했고,
- distortion이 반영된, 제대로 된 intrinsic matrix도 구했으니,
- 왜곡된 이미지를 펴보자!
# dst: 보정된 이미지
dst = cv2.undistort(src=img,
cameraMatrix=mtx,
distCoeffs=dist,
dst=None,
newCameraMatrix=newcameramtx)
x, y, w, h = roi
dst = dst[y:y + h, x:x + w]
cv2.imwrite('calibresult.png', dst)- 이미지의 해상도가 캘리브레이션 단계에서 사용된 해상도와 다른 경우,
fx와fy,cx와cy는 각각 스케일링되어야 하며, 왜곡 계수는 동일하게 유지됨
5.3.6. calibration 과정의 오차 정량적 계산하기
왜곡 제거: 이미지의 프로젝션- 이 왜곡 제거 시 수행된 프로젝션에 발생하는 오차가 얼마인지를 알기 위해
cv2.projectPoints()함수가 사용 - 결과적으로 얻어지는 값이 0에 가까울수록 정확한 것
# 에러 계산
tot_error = 0
for camera_idx in range(len(objpoints)):
# objpoint: 실제 세계의 3D 점 (H*W, 3)
# rvec: 각 패턴 뷰에 대한 회전 벡터의 튜플.
# tvec: 각 패턴 뷰에 대한 변환 벡터의 튜플.
# mtx: intrinsic matrix (3, 3) # optimal 은 아님
# dist: distortion coefficients (1, 5)
# object point를 이미지 point로 변환
imgpoints2, _ = cv2.projectPoints(objpoints[camera_idx], rvecs[camera_idx],
tvecs[camera_idx], mtx, dist)
# cv2.findChessboardCorners + cv2.cornerSubPix로 얻은 이밎 point와,
# 변환된 이미지 point와 거리 계산
error = cv2.norm(imgpoints[camera_idx], imgpoints2,
cv2.NORM_L2) / len(imgpoints2)
tot_error += error
print("total error: ", tot_error / len(objpoints))
cv2.destroyAllWindows()
예전에 intrinsic matrix를 구하려고 시도했었던 여러 방법을 공유드렸었지만 리마인드차 남겨봅니다.
opencv를 이용했던 방법중 아쉬웠던 부분을 적자면
cv2.cornerSubPix함수는 체커보드의 꼭짓점을 pixel 단위보다 fine한 subpixel 단위로 보정해주는 함수인데요, 시각화해보니 오히려 꼭짓점의 위치를 왜곡시켜버리는 효과가 있었습니다. 사용 후 제대로 적용되었는지 확인이 필요합니다.