[2022 ICLR] COSFORMER: Rethinking Softmax In Attention
[Paper Review] Efficient and Scalable
Paper Info.
1. Abstract
-
Transformer는 NLP, CV, and audio processing에서 great successes를 보여주고 있다.
-
core components로, softmax attention은 long-range dependencies를 효과적으로 capture하지만,
sequence length에 따라 space and time complexity가 quadratic 증가하여 scale-up에 제약이 있다.
이를 해결하기 위해 kernel methods가 자주 사용되어 softmax operator를 approximating하지만,
이 과정에서 발생하는 approximation errors로 인해,
vanilla softmax attention에 비해 crucial performance drops이 발생한다. -
본 논문에서는 COSFORMER라는 Linear Transformer를 제안한다.
이 model은 standard Transformer와 비교했을 때 comparable or better accuracy를 달성할 수 있으며,
Causal Attention과 Cross Attention 모두에서 효과적이다.
COSFORMER는 Softmax attention의 two key properties에 기반한다:- non-negativeness of the attention matrix
- a non-linear re-weighting scheme that can concentrate the distribution of the attention matrix
-
COSFORMER는 이러한 특성을 유지하면서도,
a linear operator와 cosine-based distance re-weighting mechanism을 활용한다.
1. Introduction
(문제 & 기존 연구)
- Dot-product attention with softmax normalization은 its quadratic space and time complexity로 인해 computational overhead가 크다.
To address this issue, numerous methods are proposed recently...
(기존 연구의 문제점)
- 하지만, 향상된 efficiency는 일반적으로 the attention matrix에 대해 아직 impractical assumptions을 도입하거나,
제한된 theoretical bounds 내에서만 softmax 연산을 approximation함으로써 달성된다.
따라서 their assumptions이 unsatisfied되거나 approximation errors가 accumulated될 경우, 이러한 방법들은 vanilla architecture에 비해 항상 유리하다고 볼 수 없다.
(motivation)
- Softmax operator가 efficient yet accurate 사이에서 주요한 장애물로 작용하며, 이를 효과적으로 approximation하는 것이 어렵다는 점에서,
one question naturally arise: "Can we replace the softmax operator with a linear function instead, while maintaining its key properties"
softmax attention을 살펴보기 전에, 우리는 softmax attention의 empirical performance에 영향을 미치는 two key properties를 발견했다:- elements in the attention matrix are non-negative (softmax로 인해 negative 값들이 사라지는 것을 말하는 듯)
- the non-linear re-weighting scheme acts as a stabilizer for the attention weight (attention 이후 FFN 말하는 듯)
- These findings는 기존 approaches에 대한 new insights를 제공한다.
예를 들어, Linear Transformer(Katharopoulos et al., 2020)는 exponential linear unit (ELU) activation function을 통해 property 1.을 달성했다.
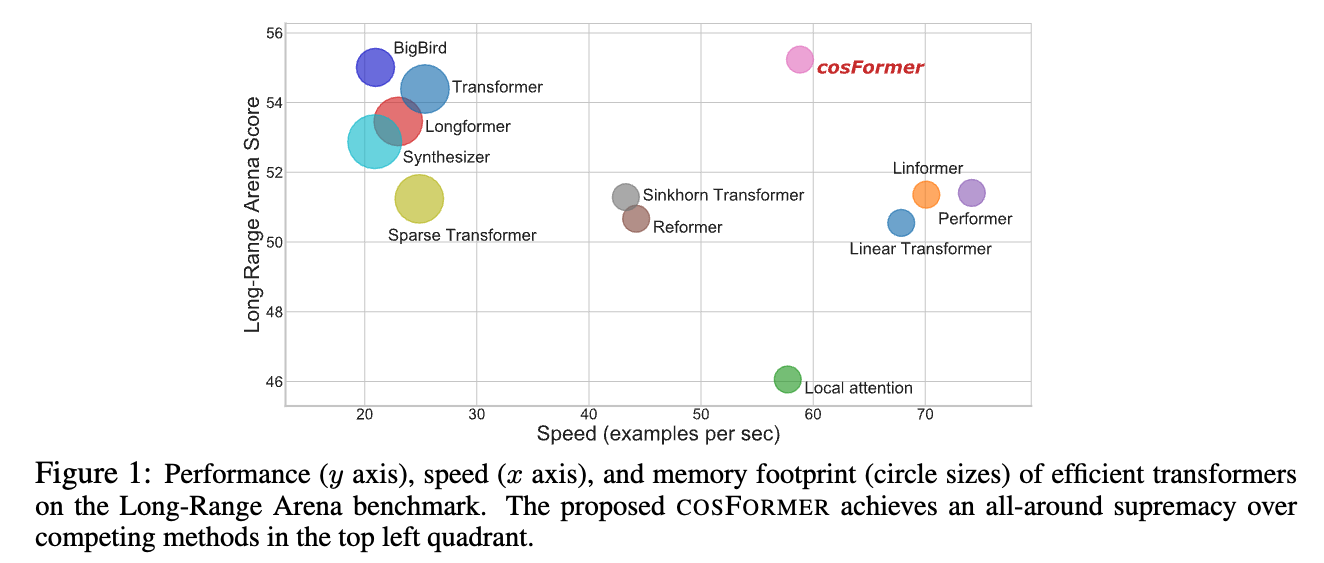
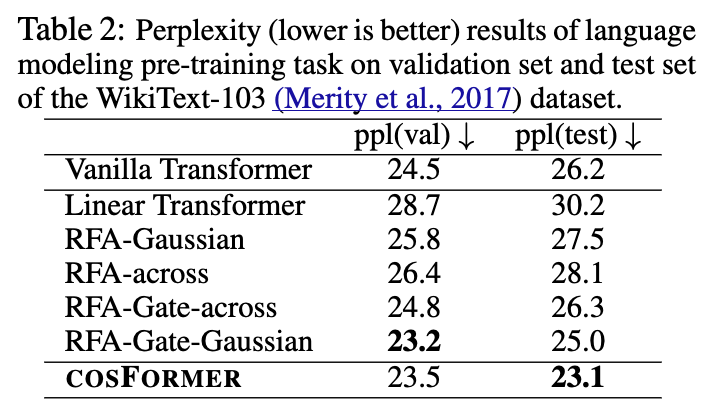
하지만 re-weight scheme은 없기 때문에, Figure 1에서처럼 Long-Rage Arena benchamrk와 the language modeling task (Table 2)에서 other efficient transformer variants보다 성능이 떨어진다.
(Ours Method)
- 본 논문에서, 우리는 앞서 언급한 두 가지 properties를 모두 만족하는 a new variant of linear transformer called COSFORMER를 제안한다.
구체적으로,- 우리는 similarity scores를 계산하기 전에 features에 ReLU activation function을 적용함으로써 non-negative property를 보장한다.
이러한 방식은 model이 negatively-correlated contextual information을 aggregating하지 않도록 유도한다. - 또한, attention weights의 stablize를 위해 cos 기반의 cos re-weighting scheme을 도입했다.
이 scheme은 NL tasks에서 중요한 local correlations을 amplify (강조)하는 데 도움을 준다.
Ptolemy's theorem 덕분에, our attention은 exactly linear form으로 decomposed될 수 있다.
(출처: https://en.wikipedia.org/wiki/Ptolemy%27s_theorem)
사각형이 원에 내접해있을 때, 아래와 같다고 한다.
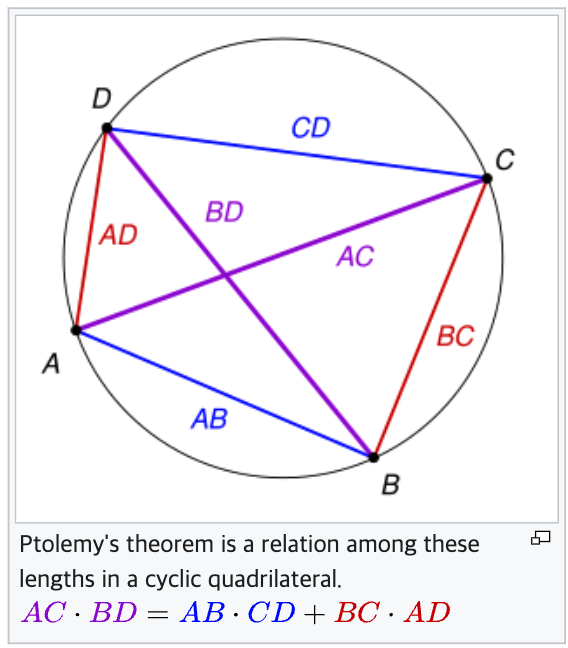
- 우리는 similarity scores를 계산하기 전에 features에 ReLU activation function을 적용함으로써 non-negative property를 보장한다.
- Our model shows much better inference speed and smaller memory footprint, while achieving on par performance with the vanilla transformer.
2. Our Method
-
이 section에서는 COSFORMER라는 우리의 linear transformer에 대한 technique details을 제공한다.
COSFORMER의 key insight는 non-decomposable non-linear softmax operation을,
decomposable non-linear re-weighting mechanism으로 대체하는 것이다. -
Our model은 causal attention과 cross attention 모두에 적용이 가능하며,
input sequence length에 대해 a linear time and space complexity를 가지므로 long-range dependency를 효과적으로 modeling하는 strong capacity를 보인다.
2.1. The General Form of Transformer
- Transformer 연산 과정에 대한 review인데, 다 아는 내용이라 짧게 쓰겠다..
짧게 요약하면,- length의 input sequence 가 있음.
를 차원으로 embedding함.
embedded 를 self-attention function 에 입력.
에 Query, Key, Value로 embedding되기 위한 learnable linear matrices 가 있음.
Q와 K의 similarity를 측정하기 위해 에 입력.
만약 라면, Eq. 2은 dot-product attention with softmax normalization이 됨.
이 경우, one row of the output 의 the space and time complexity는 이 됨.
이때, Q, K는 각각 이기 때문에 는 이 됨.
- length의 input sequence 가 있음.
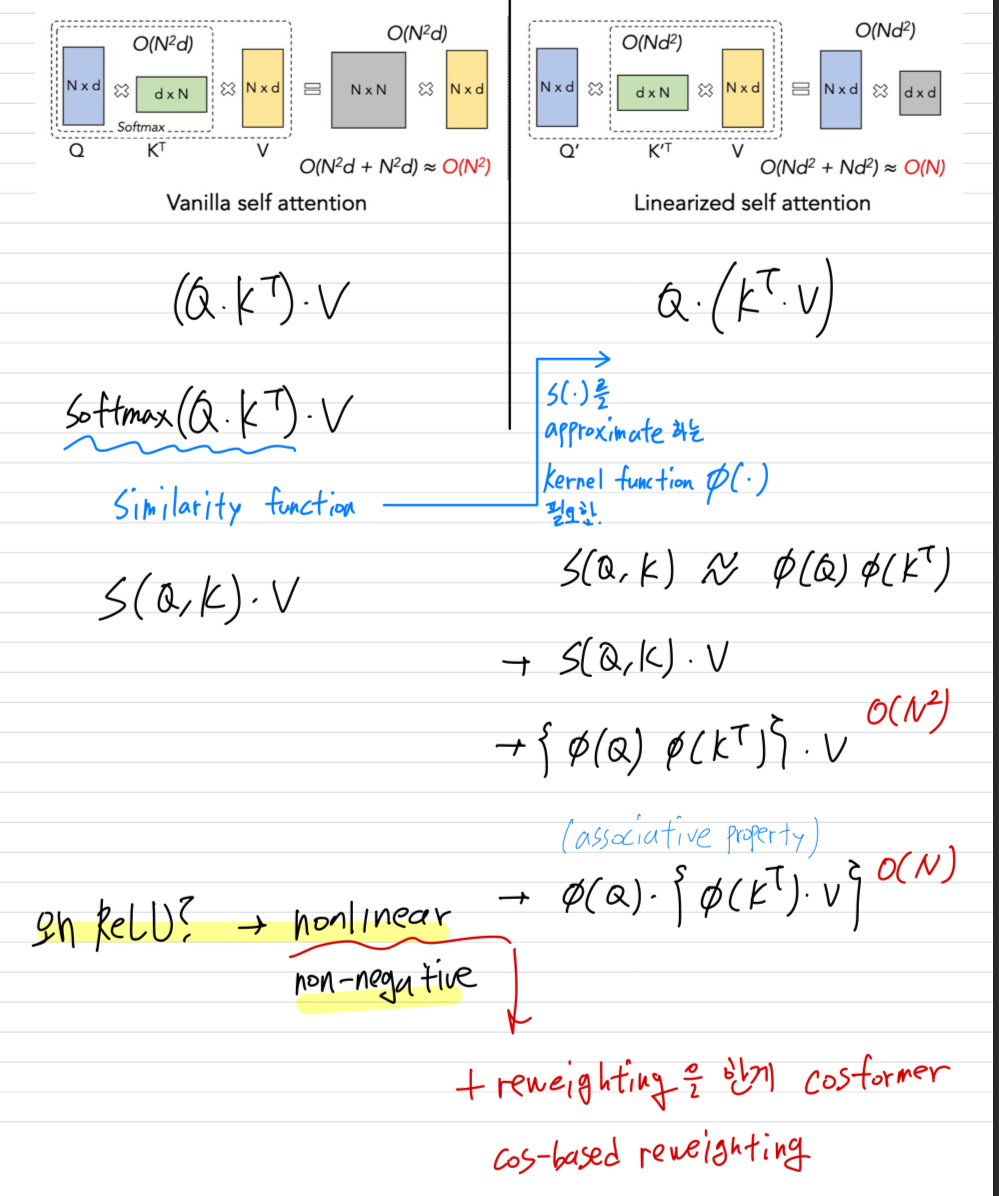
2.2. Linearization of Self-Attention
- Eq. 2에 따르면, attention matrix를 계산하기 위해 any similarity functions을 고를 수 있다.
a linear computation budget을 유지하기 위해, 하나의 solution은 아래와 같이 a decomposable similarity function을 사용하는 것이다:
 는 queries and keys를 their hidden representations으로 mapping하는 a kernel function이다. (뒤에 나오는데, nonlinear activation을 말함)
는 queries and keys를 their hidden representations으로 mapping하는 a kernel function이다. (뒤에 나오는데, nonlinear activation을 말함)
그리고나서, Eq. 2을 다음과 같은 the form of kernel functions으로 rewrite할 수 있다.
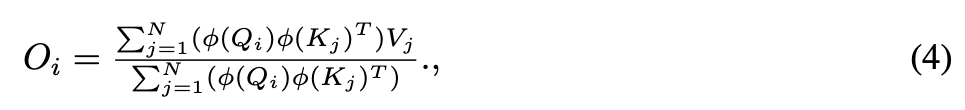 Eq. 5에서, attention matrix 을 계산하는 대신에,
Eq. 5에서, attention matrix 을 계산하는 대신에,
우리는 를 먼저 계산하고 나서 를 곱해준다.
이 trick으로, 우리는 only a computation complexity of 을 발생시킨다.
(보통 )

Previous Solutions
-
linear attentions에 대한 key는 decomposable simlarity function 을 찾는 것이다.
여러 연구들이 있었지만.... (skip) -
본 논문에서는 softmax를 대체하는 a new replacement of softax를 제안하며,
이는 다양한 task에서 softmax attention과 comparable or better performance를 달성함과 동시에,
linear space and time complexity를 갖는다는 장점이 있다.
2.3. Analysis of Softmax Attention
-
vanilla transformer architecture에서는 일 때, softmax operation이 적용되어 attention matrix 에 대해 row-wise normalization이 수행된다. (Eq. 2)
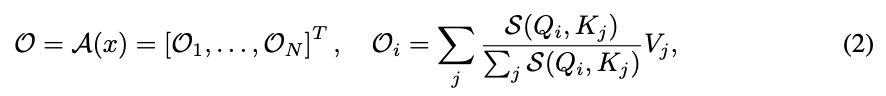 즉, input sequence의 각 element가 다른 모든 elements와 맺는 relations을 normalize함으로써, contextual information의 weighted aggregation을 계산한다.
즉, input sequence의 각 element가 다른 모든 elements와 맺는 relations을 normalize함으로써, contextual information의 weighted aggregation을 계산한다.
그러나 softmax attention이 실험적으로는 좋은 성능을 보임에도 불구하고, 그것의 핵심적이고 필수적인 특성이 무엇인지에 대해서는 the original transformer paper and follow-up works에서도 명확하게 규정되지 않았다. -
이 연구에서, 우리는 softmax operation이 performance에 중요한 역할을 하는 two key properties를 식별했다:
- it ensures all values in the attention matrix A to be non-negative
- it provides a non-linear reweighting mechanism to concentrates the distribution of attention connections and stabilizes the training.
-
위의 assumption을 validate하기 위해,
우리는 Table 1에 제시된 바와 같이 preliminary studies를 설계했다.
먼저, non-negativity의 중요성을 검증하기 위해 equation 3에서 the function 의 three instantiations (변형)을 비교한다:
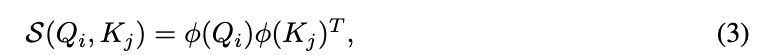
- negativity를 유지하는 identity mapping
- negativie values를 0으로 바꾸고 positive input values만 유지하는
- negative values도 보존하되 ReLU와 같은 non-linearly를 가진
-
다음으로, non linear re-weighting의 효과를 보여주기 위해,
우리는 softmax 연산 없이 만 사용하는 model과 softmax operations을 포함한 model을 비교한다.
Table 1에서 보이듯이, 가 와 보다 superior results를 보이는 것은
the benefit of retaining non-negative values를 보여준다.
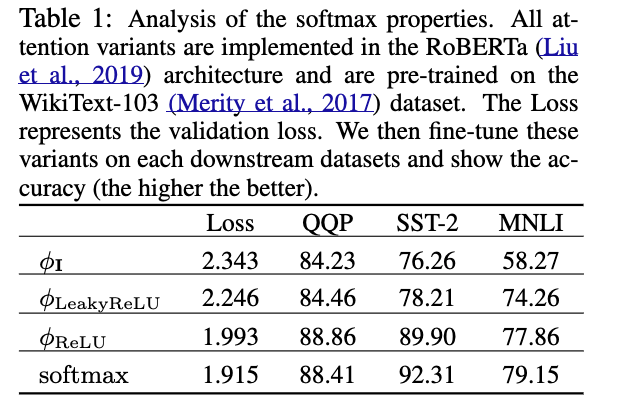
우리의 conjecture는 similarity matrices에서 positive values만 유지함으로써, model은 negative correlation을 가지는 features를 무시하게 되며,
결과적으로 irrelevant contextual information을 agregating하는 것을 효과적으로 피할 수 있다. (?)
또한 와 softmax를 비교한 결과, softmax re-weighting을 사용하는 models이 더 빠르게 converge하고,
downstream task에 better generalize되는 것을 관찰했다.
이는 softmax normalization이 correlated pairs를 증폭시켜, useful patterns을 식별하는 데 유용하기 때문일 것이다.
2.4. COSFORMER
- 위 관찰을 바탕으로, 우리는 우리의 model COSFORMER를 제안한다.
COSFORMER는 non-negativity and re-weighting mechanism을 여전히 유지하면서 softmax normalization을 완전히 없앴다.
our COSFORMER는 two main components로 구성된다:- a linear projection kernel
- a cos-Based Re-weighting mechanism
- 각 components에 대한 details을 설명하겠다.
Linear projection kernel
- Eq. 2에서 attention의 general form을 복기하고,
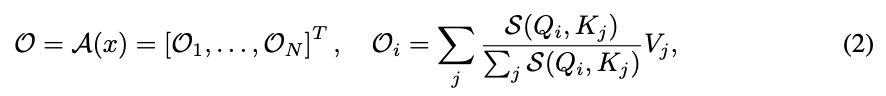
우리는 a linear similarity를 다음과 같이 정의한다:
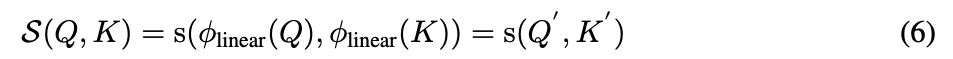 는 queries 와 keys 를 our desired representations 와 로 mapping하는 transformation function이다.
는 queries 와 keys 를 our desired representations 와 로 mapping하는 transformation function이다.
그리고 는 와 의 similarity를 측정하기 위해 linearly decomposed될 수 있는 function이다.
구체적으로, a full positive attention matrix 를 만들고 aggregating negatively-correlated information을 피하기 위해,
우리는 를 the transformation functions으로 사용했고, 효과적으로 negative values를 없앴다:

와 는 only non-negative values를 갖기 때문에,
we directly take their dot-product followed by a row-wise normalization to compute attention amtrices:
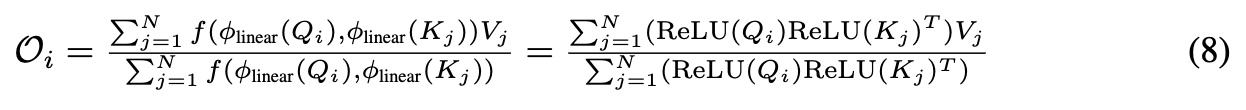 Eq. 4에 기반해서, 우리는 the order of dot-product를 rearrange하고
Eq. 4에 기반해서, 우리는 the order of dot-product를 rearrange하고
the formulation of the proposed attention in linear complexity를 얻는다: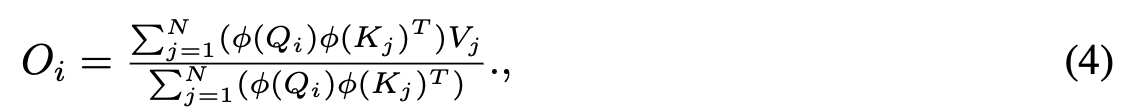
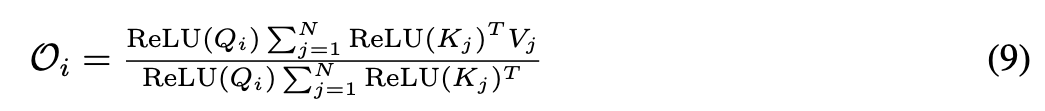
cos-Based Re-weighting Mechanism
-
softmax attention으로부터 도입되는 the non-linear re-weight mechanism은
the distribution of the attention weights에 집중할 수 있게 하고,
그렇기 때문에 training process가 stabilize하다.
우리는 또한 어떤 경우에는 far-away (멀리 떨어진) connections을 punish하여 locality를 강화한다는 것을 경험적으로 발견했다.
실제로 이러한 locality bias- 즉, 대부분의 contextual dependencies가 neighboring tokens으로부터 온다는 특성은 downstream NLP tasks에서 일반적으로 관찰된다.
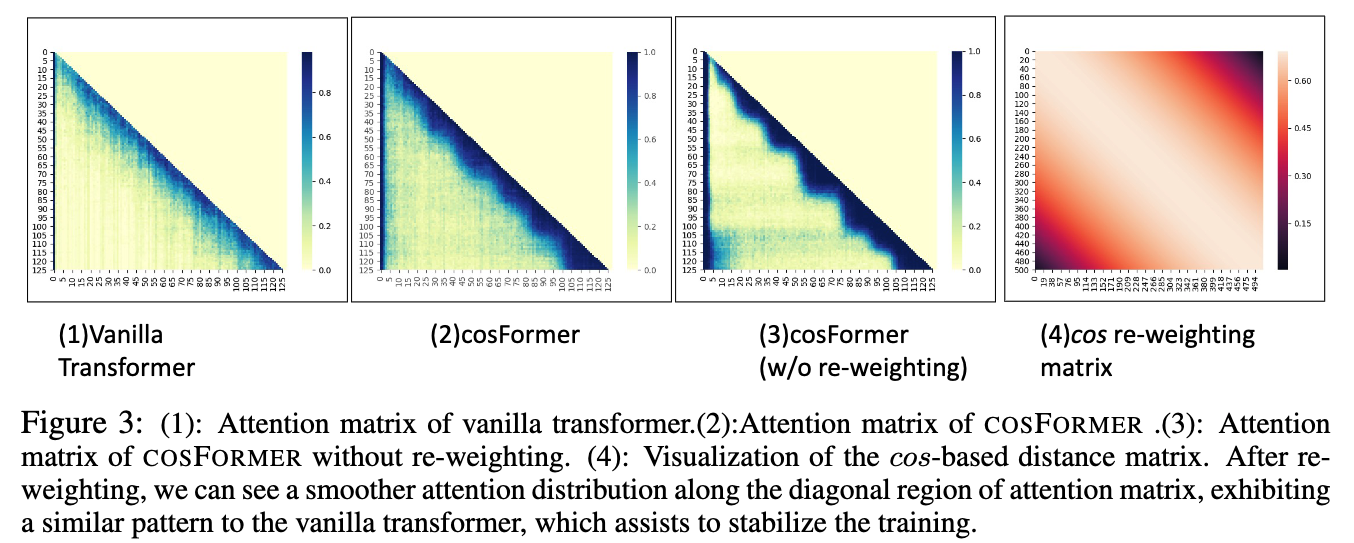
이는 Figure 3 (1)에서도 확인할 수 있다.
-
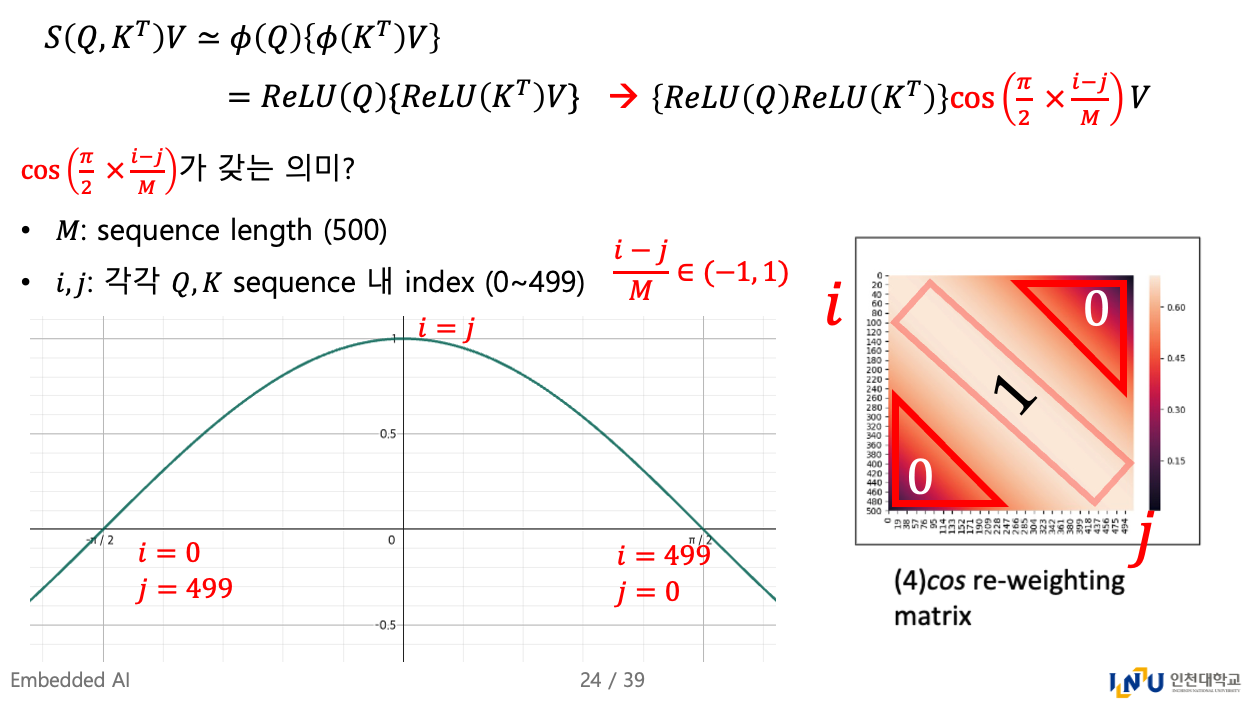
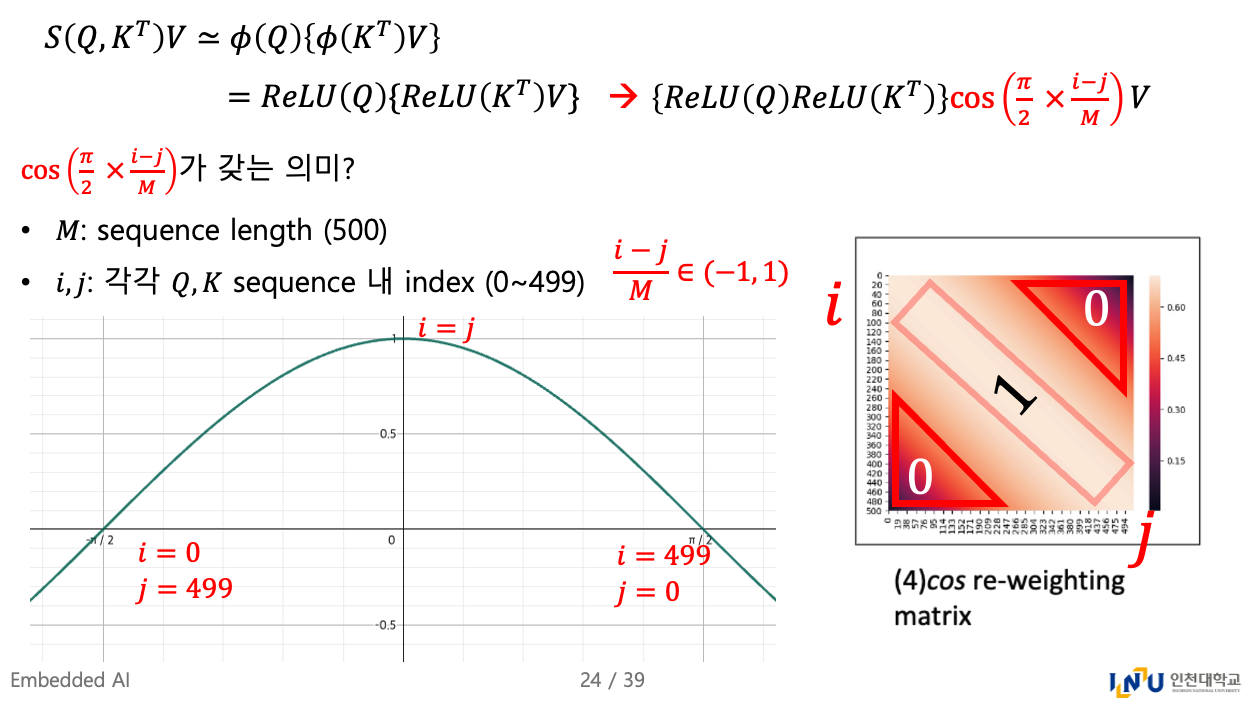
위 assumption을 바탕으로, softmax의 second property를 만족시키기 위해 필요한 것은 attention matrix에 recency bias (최근 정보 bias)를 도입할 수 있는 a decomposable re-weighting mechanism이다.
여기서 우리는 우리의 목적에 부합하는 cos-based re-weighting mechanism을 제안한다:- Ptolemy's therem에 따르면, cos weights는 two summations으로 decomposed될 수 있다.
- Figure 3 (4)에서 보이듯이, cos는 neighbouring tokens에 더 많은 weights를 부여하여 locality를 유도한다.
또한 Figure 3 (2)와 (3)의 attention matrices를 비교해보면, cosFormer는 re-weighting mechanism이 없는 경우보다 more locality를 갖는 것을 확인할 수 있다.
-
구체적으로, Eq 6를 결합함으로써, the model with cosine re-weighting은 다음과 같이 정의한다:
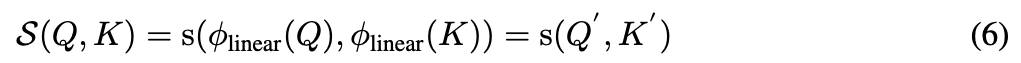
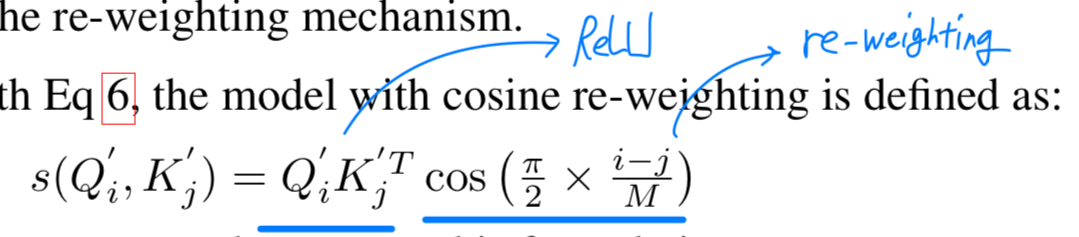 re-weighting이 갖는 의미는 뭘까...?
re-weighting이 갖는 의미는 뭘까...?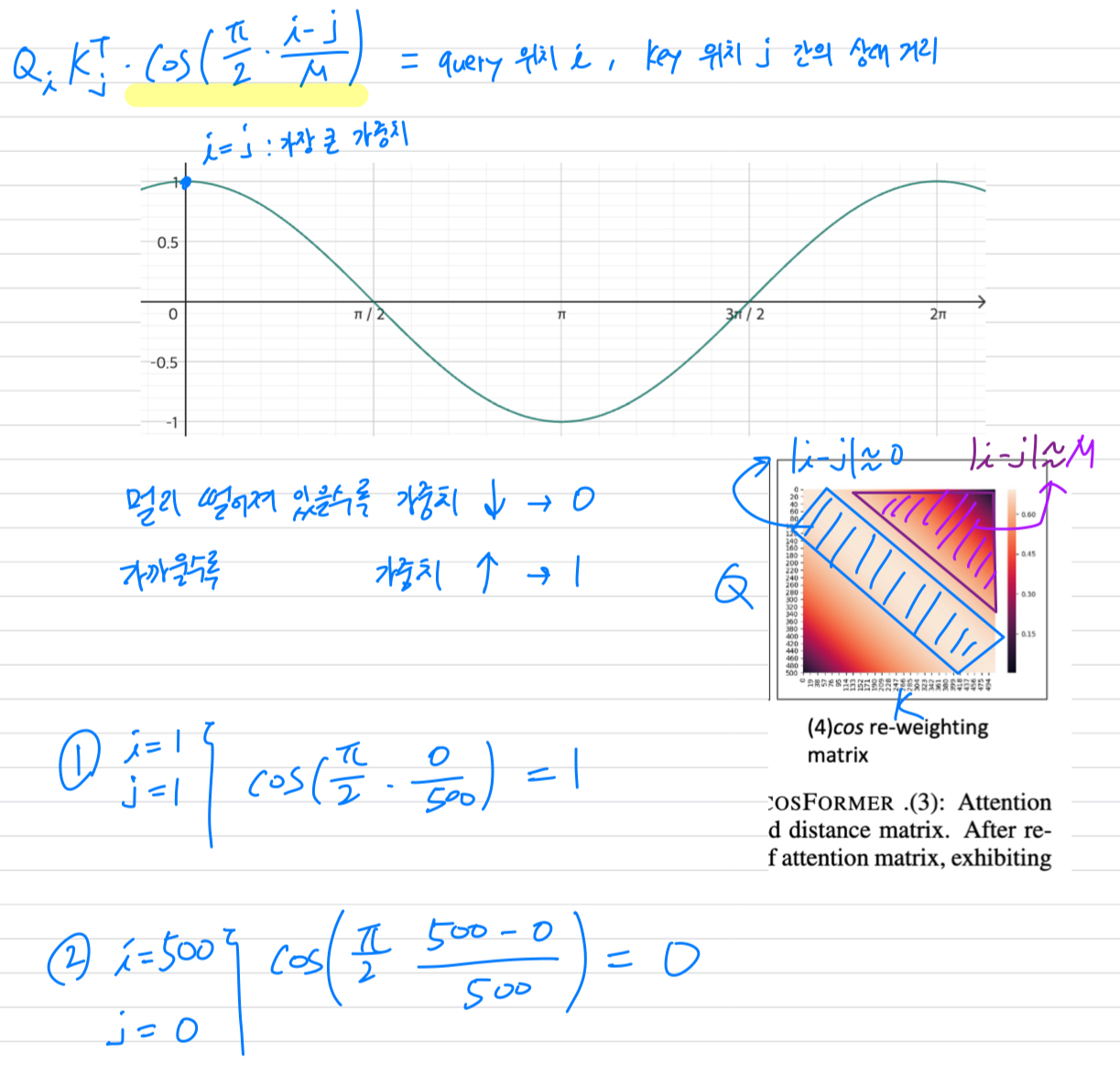
Ptolemy's theorem에 의하여, 우리는 이 formulation을 다음과 같이 decompose한다:
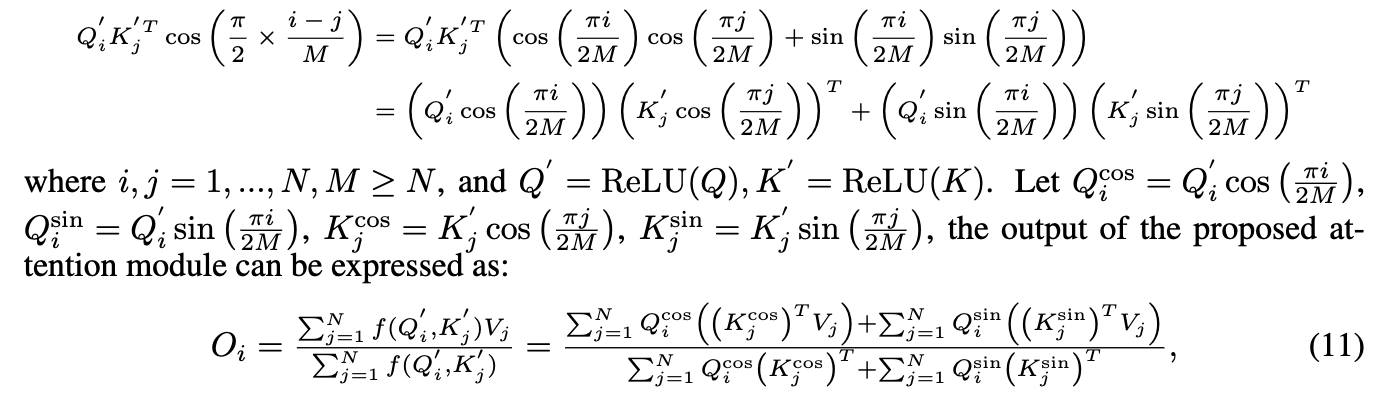
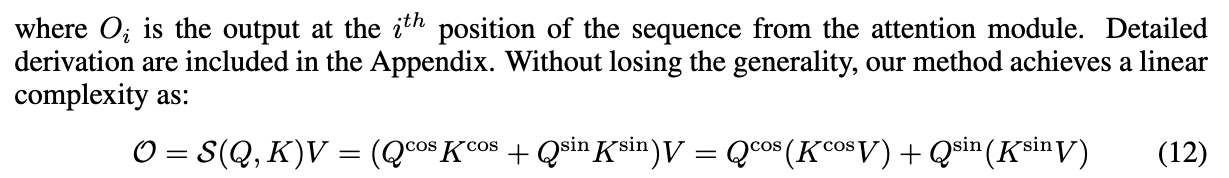
5. Conclusion

Summary
- softmax-based similarity function이 갖는 특징
- attention matrix are non-negative
- non-linear re-weighting scheme
- ReLU-based linear similarity function은 softmax-based similarity function이 갖는 특징의 대부분을 활용할 수 있음.
- attention matrix are non-negative
- non-linear, but not yet re-weighting scheme...
- CosFormer는 ReLU-based linear simlarity function의 2.에서 re-weighting scheme이 없는 것을 보완하기 위해 cos-based re-weighting mechanism을 제안함.
- attention matrix are non-negative
- non-linear, -based re-weighting scheme
그래서 cos-based nonlinear re-weighting을 어떻게 했는데?
인접한 token에는 1에 가까운 weighting, 멀리 떨어져 있는 token에는 0에 가까운 weighting.
몰랐던 것
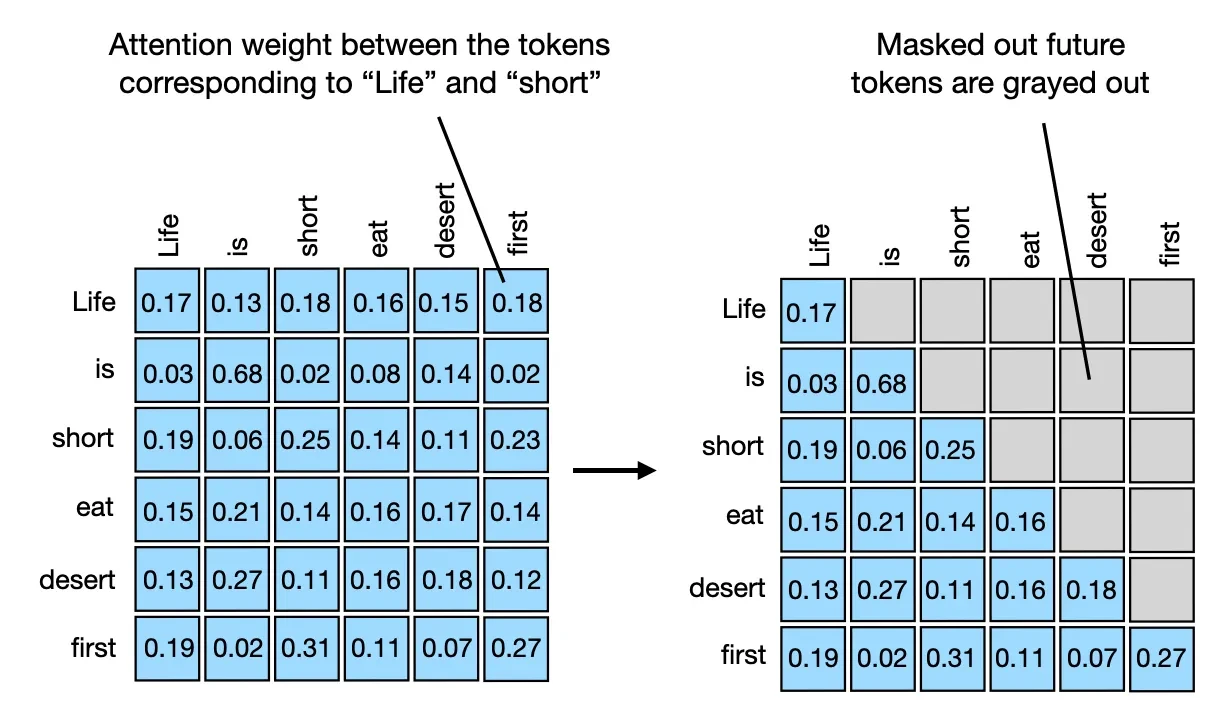
- Causal attention: 자기 자신과 이전 token들만 참조 가능
텍스트 생성 시 현재 단어는 미래 단어를 참조하면 안 되기 때문.
그래서 GPT와 같은 autoregressive 모델에서 사용.
(참고: https://www.kaggle.com/code/aisuko/causal-self-attention)