Localization
SLAM
-
SLAM: Simultaneous Localization And Mapping.
자율주행 차량을 비록한 로봇에 사용되어 미지의 주변 환경 지도를 작성하는 동시에
차량의 위치를 작성된 지도 안에서 추정하는 방법. -
절대적인 차량의 위치는 알 수 없으니까
미리주행하며 얻은 LiDAR data로 만든 3D Map과
또 다시 주행하며 얻은 LiDAR data랑
특정 부분에서 일치하는 지점을 통해
현재 내가 어디에 있는지 추정할 수 있다.
➡️ 그것을 통해서 위치를 찾음(Localization) -
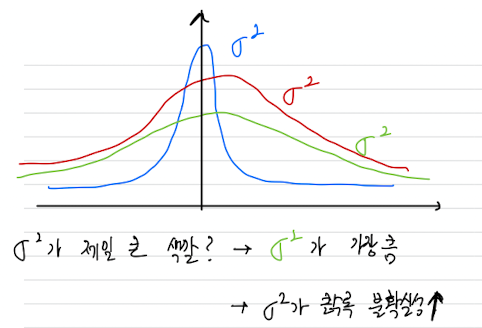
Localization을 바라보는 입장:
내가 그곳에 존재하는 것이 아니라, 그곳에 존재할 확률이 있다. 정해진 것이 아니다.
➡️ Gaussian Distribution으로 에 의해서 결정이 난다.
➡️ 따라서 Autonomous Driving은 Probablistic Robotics의 한 분야이다.
-
ex. Steering Wheel이 정확히 0에서 직진한다. 똑바로 직진할까?
No.
➡️ 도로에 한쪽에는 물, 한쪽에는 물 없는 경우
➡️ 바퀴가 편마모되어 있는 경우
➡️ 도로에 경사가 있는 경우
➡️ 탑승자가 한쪽에 몰려있는 경우
➡️ Sensor에 noise
➡️ 차의 섀시가 움직여 LiDAR 정보에 왜곡
등.. 의 이유로 똑바로 직진한다는 보장이 없음이것이 Sensor의 한계이고 현대는 HD Map based SLAM을 통해 자율 주행.
자율주행의 SLAM에서부터 시작된다.
-
-
Lidar, GPS, IMU를 통해 odometry를 계산하고 Lidar를 통한
Loop Closure를 통해 위치를 추정
(odometry : 차량 주행거리 측정)
(Loop Closure : 한 바퀴 돌고 나서 또 한바퀴 돌아 보정을 통해 개선해나감)
Odometric Localization
Dead Reckoning(DR)
Dead Reckoning:
차량이 최초 위치에서 주행하면서 heading과 speed 등의 주행정보를
센서 (IMU 등)를 통해 읽고 자신의 위치를 추측하는 것.
ex) 지하 주차장에서 GPS가 안될 때, Dead Reckoning을 통해 차량 위치 Localiazation
but. 방지턱을 넘을수록, 시간이 지날수록 오차가 누적되어 부정확해질 수 있다.
Velocity, Speed, Rotational Velocity
-
Velocity: 속도 (vector)
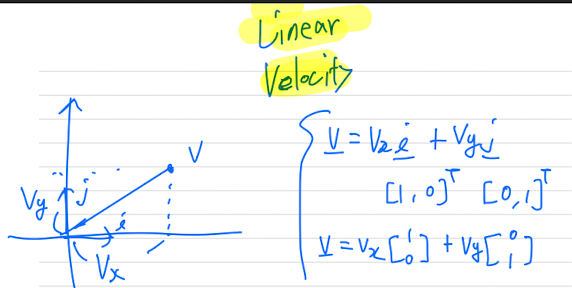
-
Speed: 속력 (scalar)
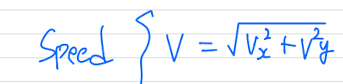
-
Rotational Velocity: 각속도 == 각속력
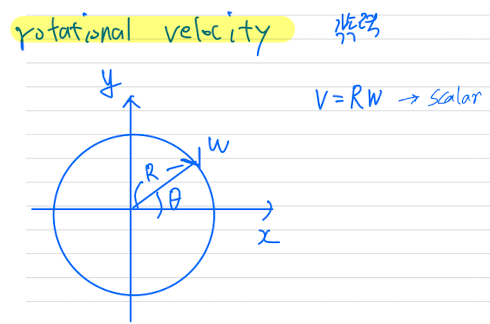
-
보통 CAN 통신은 1초에 100번 차량의 data(: velocity, : steering angle = yaw angle)가 들어옴.


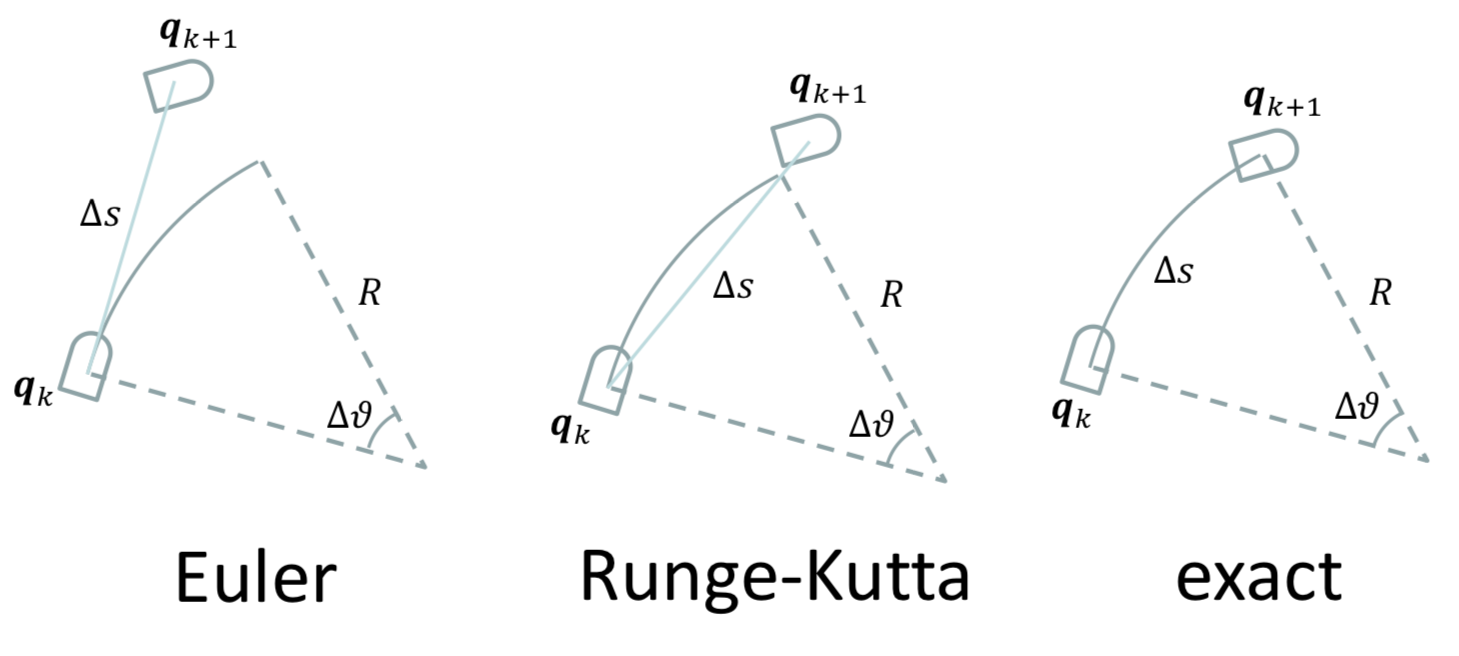
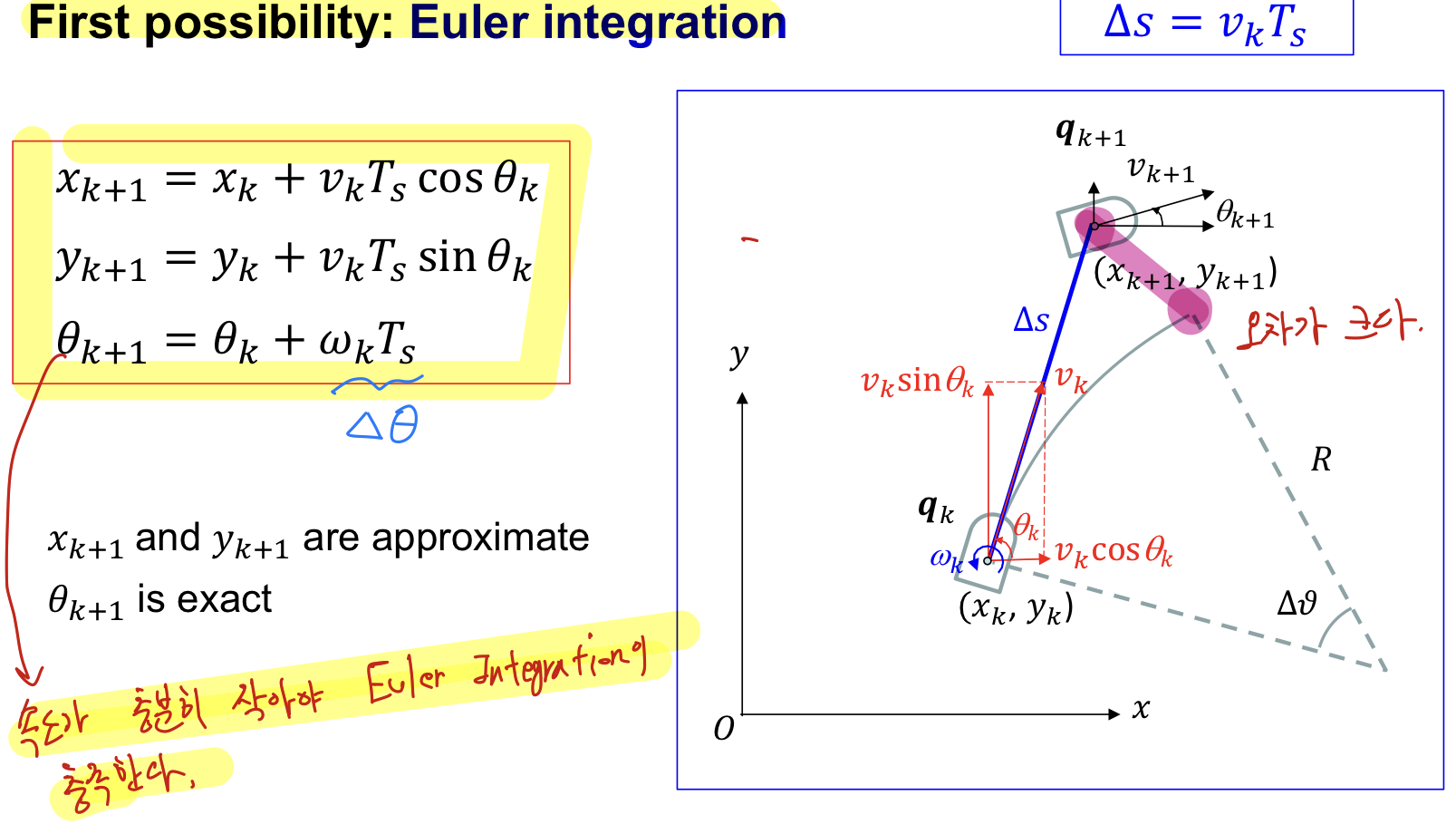
1. First Possibility : Euler Integration
Euler Integration
: Vehicle 속도가 충분히 작아야 Euler Integration이 충족한다.
속도가 느릴 때는 사용할 수 있지만, 속도가 빨라지면 오차가 커져 문제가 발생한다.
2. Second Possiblity : 2nd order methodRunge-Kutta Integraion
Runge-Kutta Integration
: Runge-Kutta가 복잡한 미분방정식을 간단히 하여
➡️
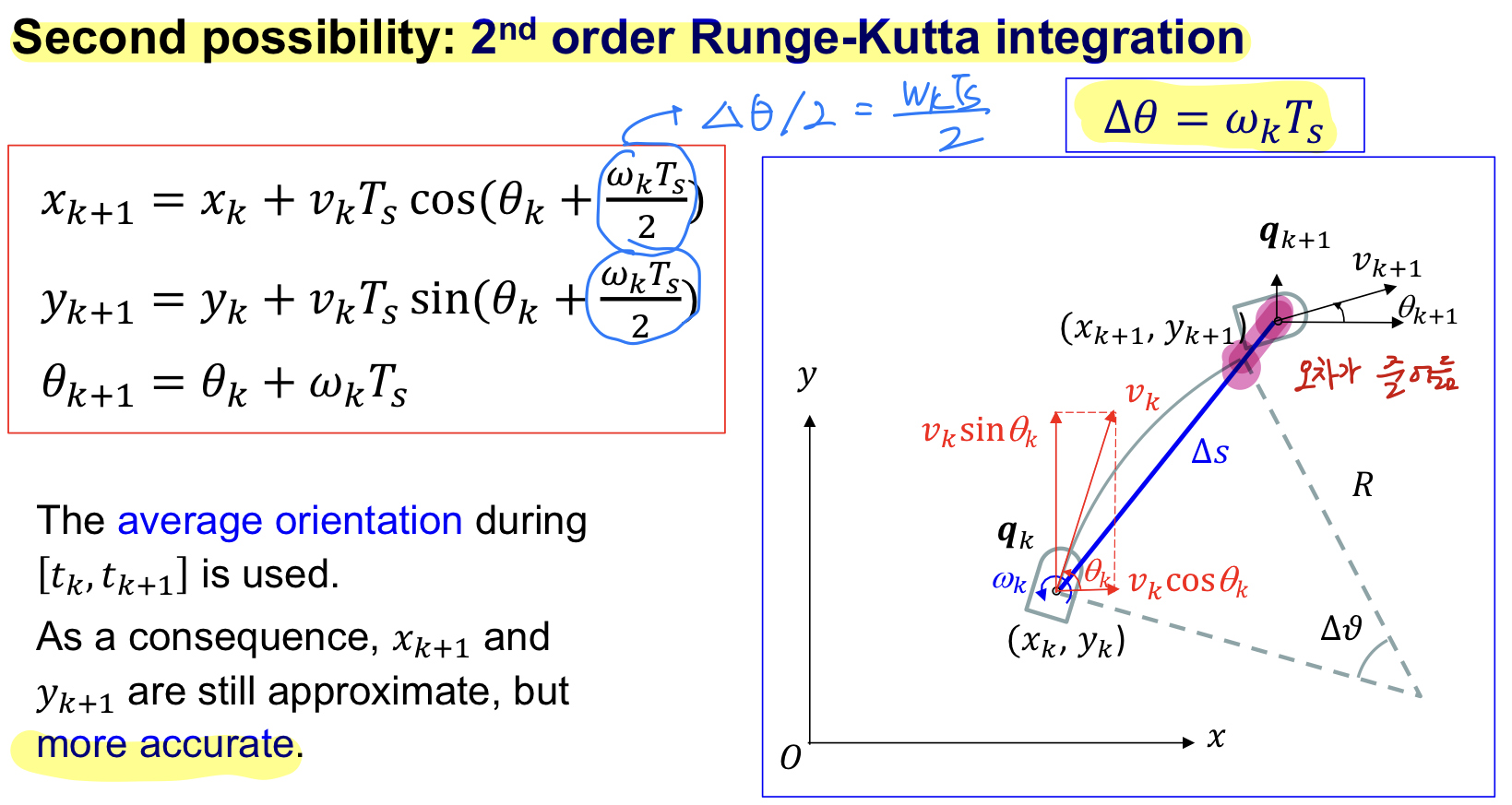
가 커지면, Euler Integraion 대신에 Runge-Kutta를 사용해야 한다.
3. Third Possibility : Exact Integration
-
Exact Integration: 오차가 가장 작다. -
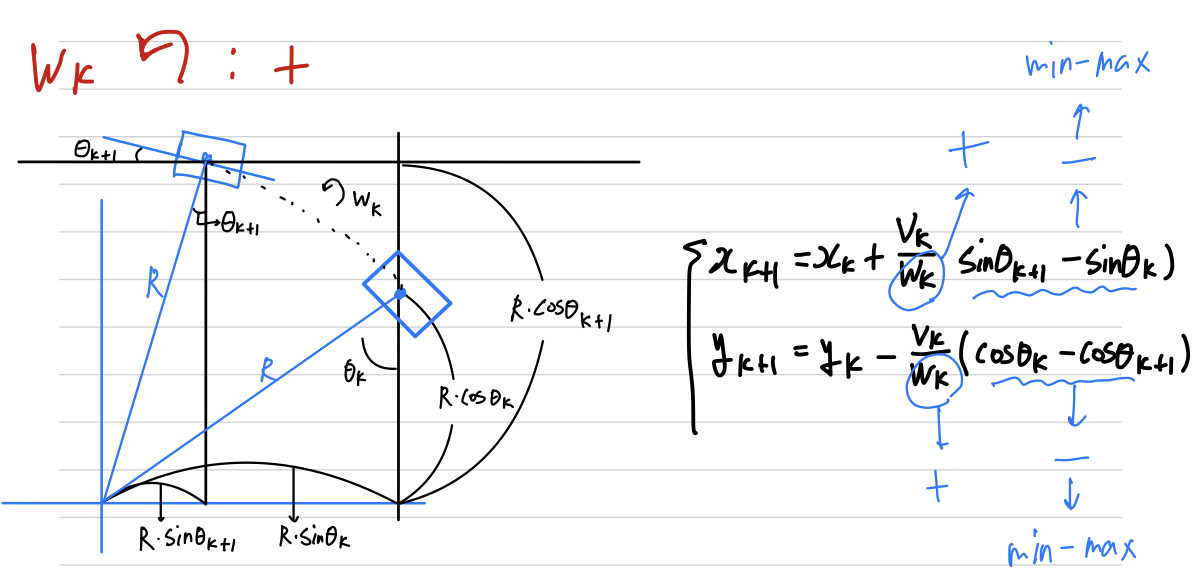
아래 상황은 좌회전하는 yaw 회전을 +로 초기 설정해놨다.
따라서 , 가 맞다.
만약 우회전하는 yaw 회전을 +로 초기 설정해놨다면,
, 이 맞다.
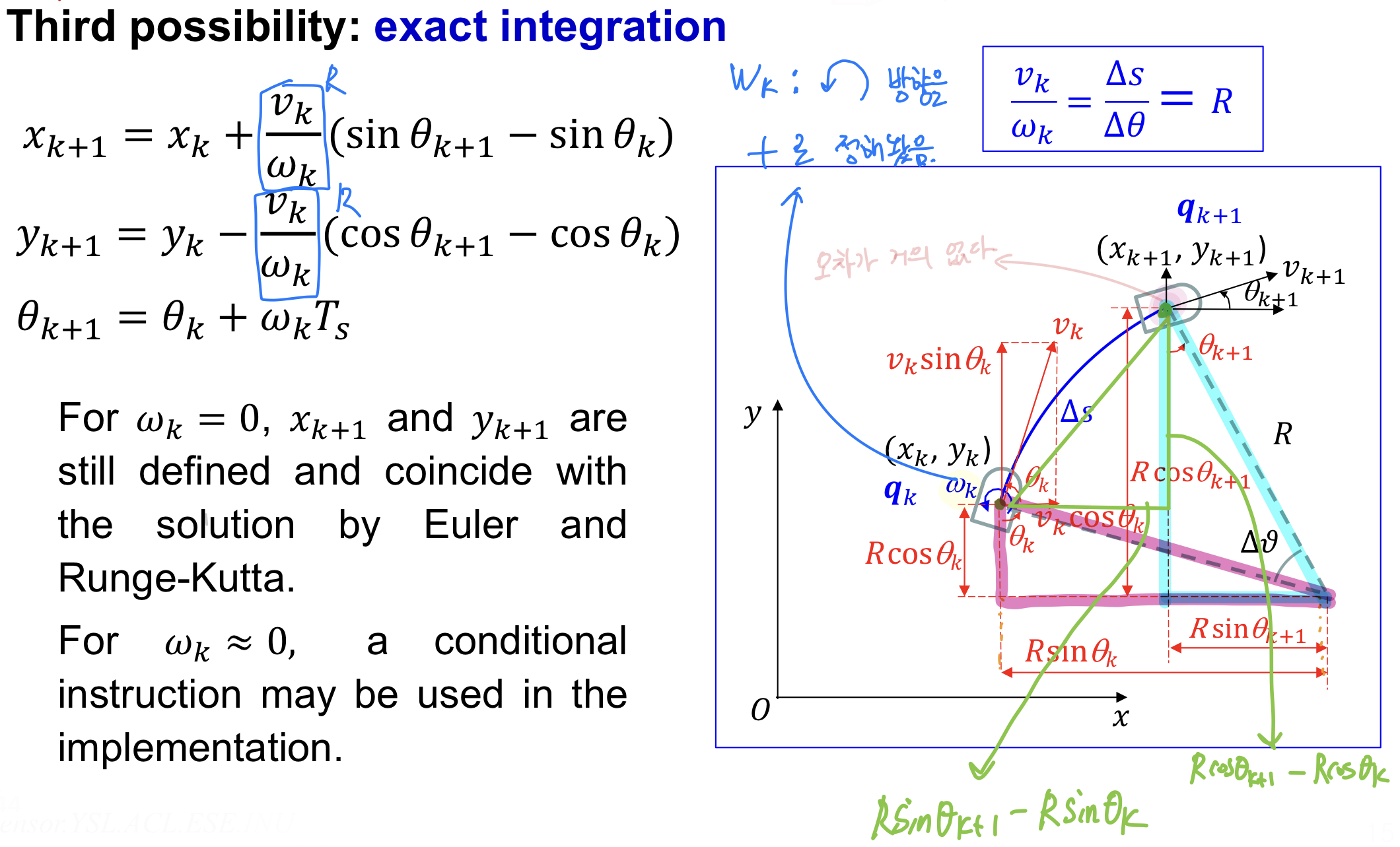
-
만약 좌회전하는 yaw회전을 +로 하였고, 차량이 좌회전을 하고 있을 때의 Exact Integration을 유도하라.
Euler vs Runge-Kutta vs Exact
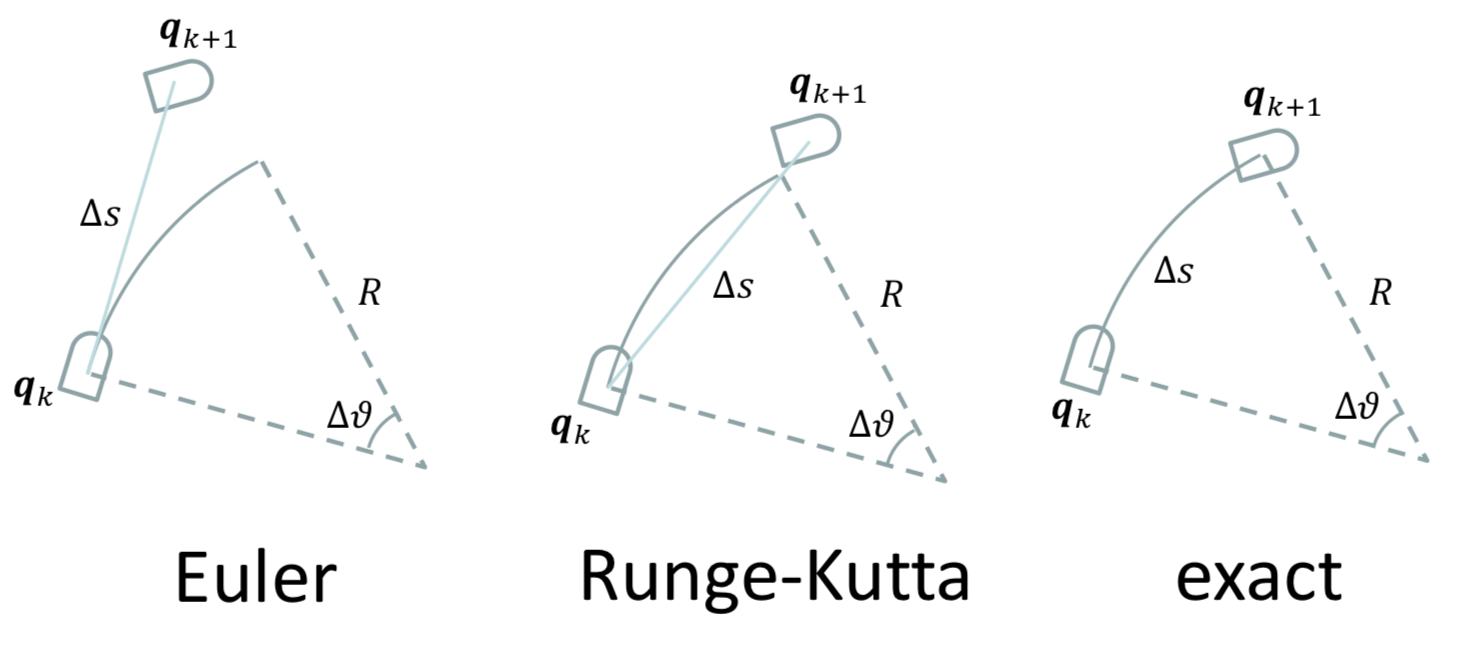
- Euler는 차량 속도가 느릴 때, 적용 가능하지만 빠를 때는 오차가 커서 문제 발생.
- 가장 정확한 것은 Exact Integration이다.
실습
-
주행하며 얻은 Lidar data와 Dead Reckoning을 통해 SLAM
: https://github.com/LeeHyungSeop/3-1_SensorAndActuator/tree/main/11weekth_DeadReckoning -
Euler, Runge-Kutta, Exact 방식마다 x, y, theta, velocity의 Error값 계산 & 시각화
https://github.com/LeeHyungSeop/3-1_SensorAndActuator/tree/main/HW_04