Paper Info.

• CVPR 2017
  

Abstract

• 우리는 image classification을 위한 간단하고, 잘 modularized된 network architecture를 제안한다.
  이 network는 동일한 topology를 가진 a set of transformations을 aggregate한 building block이 반복되어 구성된다.
  이러한 단순한 설계는 only a few(적은) hyper-parameters만 설정하면 되는 homogeneous(균일), multi-branch architecture를 만들어낸다.

• 이 strategy는 "Cardinality" (the size of the set of transformations, 변환 집합의 크기)라는 새로운 dimension을 노출하는데,
  이는 network의 depth and width 외에 중요한 요소이다.

• ImageNet-1K dataset을 통해 우리는 complexity를 유지하는 제한된 조건 하에서도 Cardinality를 증가시키면 classification accuracy가 향상된다는 것을 보여준다.
  또한, model의 capacity를 증가시킬 때 Cardinality를 확장하는 것이 depth or width를 늘리는 것보다 더 효과적임을 확인했다.

1. Introduction

• architectures를 designing하는 것은 늘어나는 hyper-parameters(width, filter sizes, strides, etc.) 개수 때문에 점점 어려워지고 있다.
  VGG-nets은 같은 모양의 building block을 쌓아 deep networks를 만든 단순한 strategy로 인해 여전히 효과적이다.
  같은 topology의 modules을 쌓은 ResNets도 위 전략을 이어받았다.

• 이 논문에서는 VGG/ResNet의 layer repeating 전략을 채택하면서,
  split-transform-merge strategy를 쉽고, 확장가능한 방식으로 활용하는 단순한 architecture를 제안한다.

• 우리 network의 module은 low-dimensional embedding에서 각각 수행되는 일련의 transformations을 처리하며,
  이들의 outputs을 summation하여 aggregate한다.
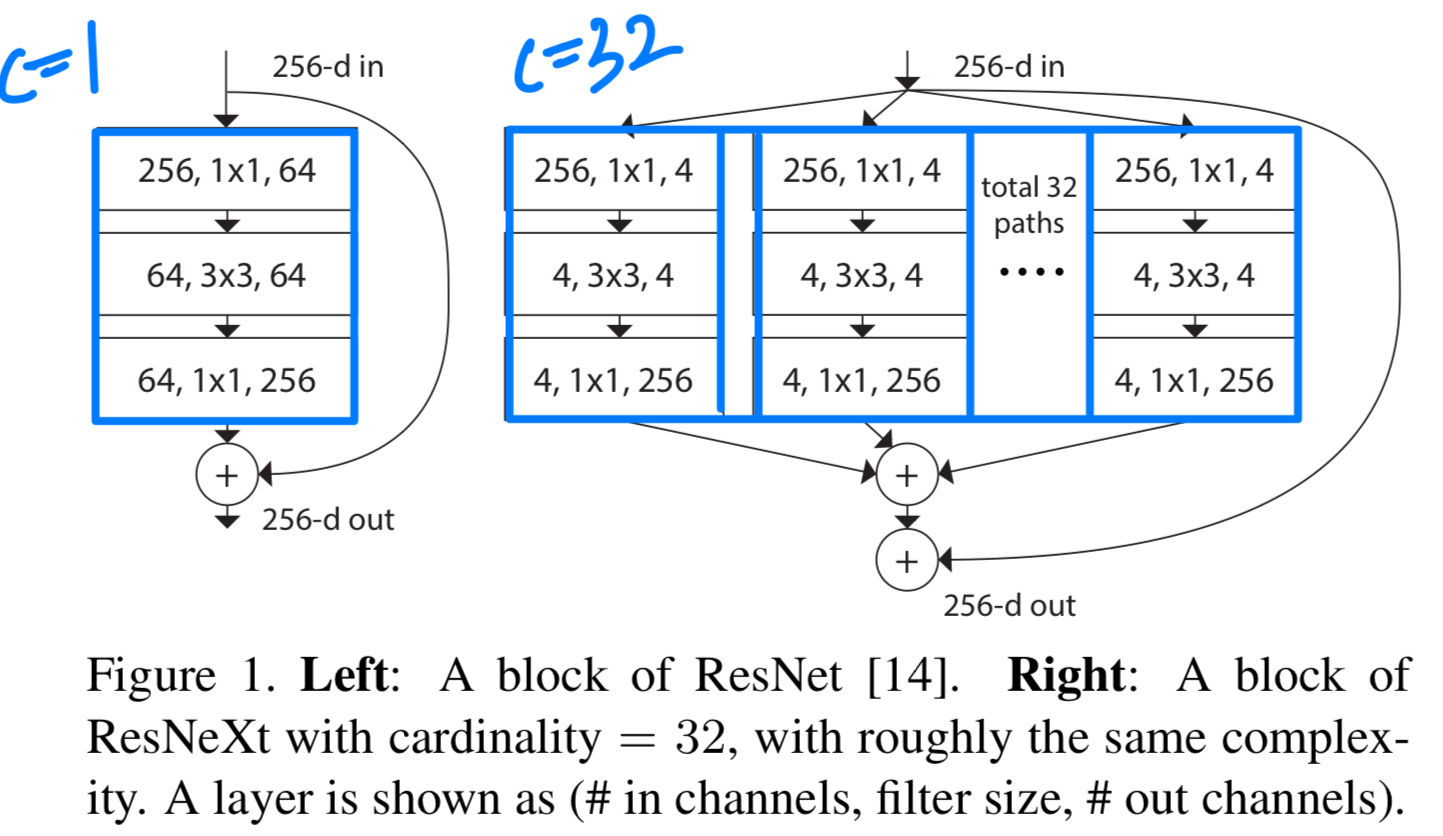
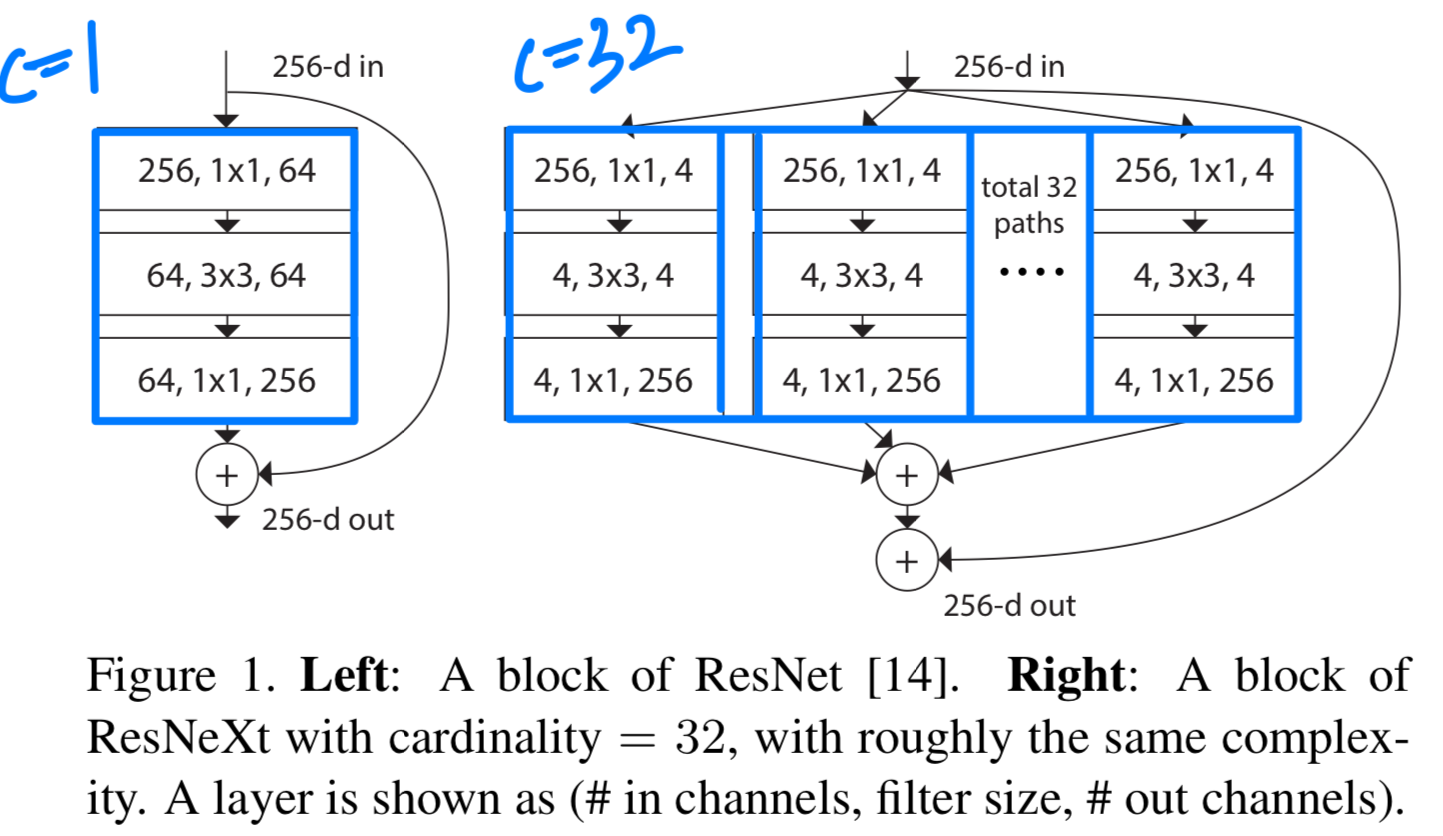
  이 아이디어를 단순하게 구현하기 위해, aggregate되는 모든 transformations은 동일한 topology를 가지도록 설계했다.
  (예, Fig.1 (right)) 이러한 설계는 특수한 설계 없이도 많은 변환을 손쉽게 확장할 수 있게 함
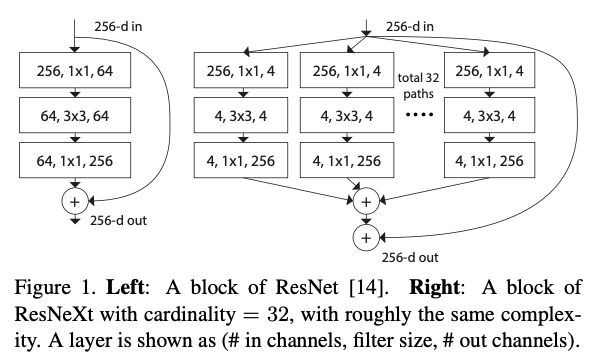  이러한 단순한 구조 하에서 우리 model은 두 가지 equivalent (동등한) 형태로 재구성될 수 있다 (Fig. 3).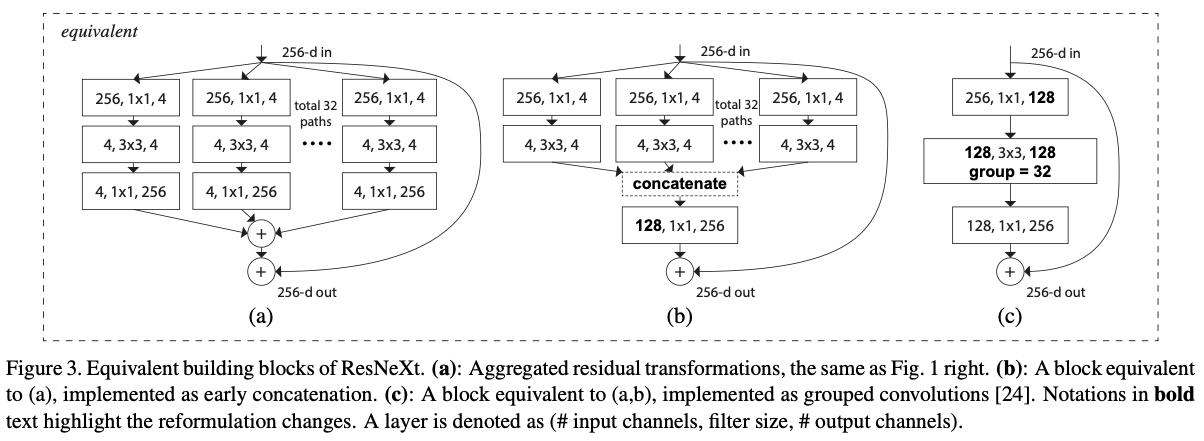Figure 3(b)에 제시된 reformulation 방식은 Inception-ResNet module [37]과 유사해 보이는데, 이는 여러 paths를 concatenate하기 때문이다.
  그러나 우리 module은 모든 path가 동일한 topology를 공유한다는 점에서 기존 Inception module과 다르며, 따라서 path의 수를 독립 변수로 간편하게 조정할 수 있다.
  더 간결한 형태로, 우리 module은 Krizhevsky et al.'s의 grouped convoluitons [24]을 통해 reformulation될 수 있다. (Figure 3(c))
  다만, grouped convolution은 본래 engineering compromise(타협)으로 개발된 방식이다.

• 우리의 방법은 cardinality, 즉 transformations 집합의 크기가
  width와 depth dimension 외에도 중요한 핵심 요소로 작용하는 구체적이고, 측정 가능한 dimension임을 보여준다.
  실험 결과에 따르면, 기존 model에서 depth and width가 점점 수익 감소(diminishing returns) 를 주기 시작할 때,
  depth and width을 확장하는 것보다 cardinality를 증가시키는 것이 정확도를 향상시키는 데 더 효과적인 방법임이 입증되었다.

  • diminishing returns란?
    수익 감소 또는 한계 효용 체감이라는 경제 용어.
    depth랑 width를 계속 늘리면 처음에는 정확도가 빠르게 향상되지만, 일정 지점을 넘어가면 성능 향상의 폭이 점점 작아지고 결국 성능 개선이 되지 않거나 오히려 악화되는 현상.

3. Method

3.1. Template

• 우리 network는 residual blocks으로 구성되어 있다.
  이 blocks들은 같은 topology를 가지고, VGG/ResNets에서 영감받은 두 가지 간단한 rules의 영향을 받았다.

  1. spatial maps의 크기가 동일한 경우, block들은 동일한 hyper-parameters (width and filter sizes)를 공유한다.
  2. spatial maps이 2배로 downsampling될 때마다, 해당 block의 width는 2배로 증가한다.
     (FLOPs 기준으로 모든 block의 computational complexity가 대략적으로 동일하게 유지되도록 보장)

• 이 두 가지 규치을 적용하면, 우리는 단순히 template module 하나만 설계하녀 되고,
  network 내의 모든 module은 이 규칙에 따라 결정할 수 있다.
  따라서 이러한 규칙은 design space를 크게 축소시켜, 몇 가지 key factors에 집중할 수 있게 해준다.

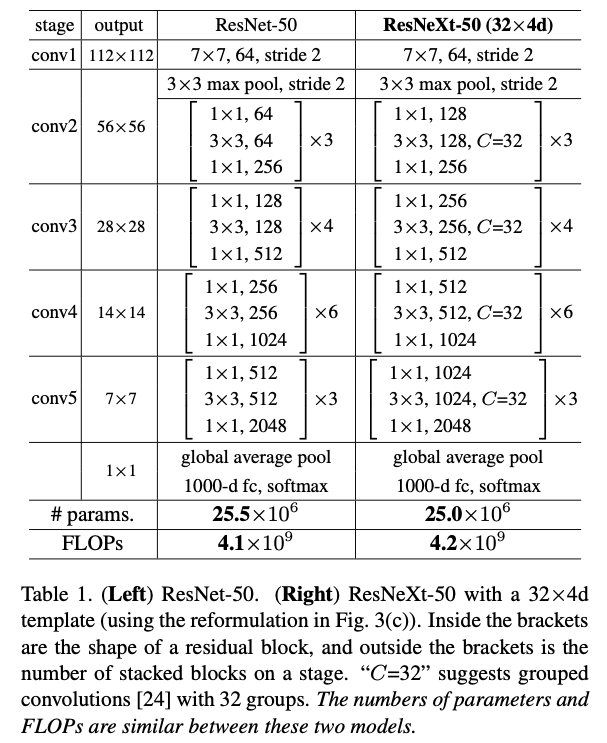
• 이 rules에 따라 구성된 networks는 Table 1에 나와 있다.
  

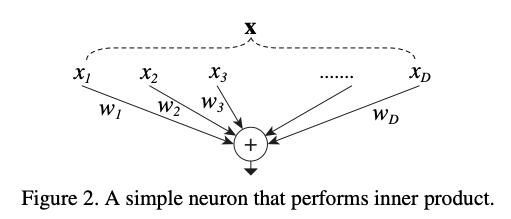
3.2. Revisiting Simple Neurons

• inner product는 일종의 aggregating transformation으로 볼 수 있다:
  위 연산을 다음과 같은 단계로 재구성할 수 있다:
  1. Splitting: vector $x$를 low-dimensional embedding으로 slice하고, 그 single-dimension subspace를 $x_i$라고 한다.
  2. Transforming: low-dimensional representation은 transformed되고, 위에서, 이는 간단히 scaled되는: $w_ix_i$
  3. Aggregating: 모든 embeddings에서 transformations은 $\sum^D_{i=1}$에 의해 aggregated된다.

3.3. Aggregation Transformations

• 위 simple neuron의 분석에 기반하여, 우리는 기초의 transformation $(w_ix_i)$을 더 일반적인 function으로 바꿀 수 있다.
  이 함수 자체도 하나의 network가 될 수 있다.
  "Network-in-Network"가 dimension of depth를 증가시키는 반면,
  우리는 우리의 접근 방식인 "Network-in-Neuron"이 new dimension으로 확장된다는 것을 보여준다.

• 공식적으로, 우리는 aggregated transformations을 다음과 같이 표현한다:
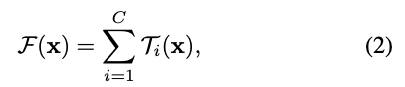  여기서 $T_i(x)$는 임의의 function이 될 수 있다.
  단순한 neuron과 유사하게, $T_i$는 $x$를 project한 후 transform한다.
  
  Eqn.(2)에서 $C$는 aggregated할 the size of the set of transformations이다.
  우리는 $C$를 cardinality라 한다.
  Eqn.(2)에서 $C$는 Eqn.(1)에서의 $D$와 비슷한 위치에 있지만, $C$는 반드시 $D$와 같을 필요가 없으며 임의의 값일 수 있다.
  width는 단순한 transformations (inner product)와 관련이 있는 반면,
  우리는 cardinality dimension이 더 복잡한 transformations의 개수를 제어한다고 주장한다.
  실험을 통해 cardinality가 중요한 dimension이며, width and depth보다 더 효과적일 수 있음을 보였다.

  • 내가 이해한 cardinality: path 하나하나가 cardinality의 한 dimension인듯
    (Cardinality가 32개 dimension을 가지면, path는 32개)

핵심 :
기존 ResNet은 cardinality 차원이 1인 하나의 single path를 가짐.
Mixture-of-Experts와 유사한 원리인듯함
하나의 convolution layer를 여러 group convolution layer로 나누어서 병렬 처리 후 마지막에 aggregate함