https://arxiv.org/abs/2303.05015

Paper Info

• Deng, Jieren, et al. "Smooth and Stepwise Self-Distillation for Object Detection." 2023 IEEE International Conference on Image Processing (ICIP). IEEE, 2023.

Abstract

• 구조화된 정보가 포함된 feature map을 distilling하는 것은 object detection task에서 결과를 개선하는 데 기여돼왔지만,
  baseline architecture의 신중한 선택과 상당한 pre-training이 필요하다.
  self-distillation은 이러한 limitation을 해결하며,
  최근 몇 가지 단순화된 architecture assumption을 만들었음에도 불구하고 object detection에서 SOTA 성능을 달성했다.

• 이 연구를 기반으로 우리는 object detection을 위한 Smooth and Stepwise Self-Distillation(SSSD)을 제안한다.
  우리의 SSSD architecture는
  object label과 feature pyramid network backbone에서 implicit(암묵적인) teacher를 형성하여
  Jenson-Shannon distance를 사용하여 label-annotated feature maps을 distill한다.
  이는 이전 작업에서 사용된 distillation loss보다 훨씬 더 smooth하다.
  또한 learning rate에 따라 적응적으로 구성된 distillation coefficient(계수)를 추가했다.

• 우리는 COCO 데이터셋에서 SSSD를 baseline model과 두 가지 SOTA object detector architecture에 대해 다양한 coefficients와 backbone 및 detector network를 변경하면서 광범위하게 benchmarking했다.
  experimental setting 대부분에서 SSSD가 higher average precision을 달성하고, a wide range of coefficients에 robust하며, 우리의 stepwise distillation procedure의 이점을 보여준다.

1. Introduction

• object detection은 knowledge distillation과 관련 작업에 대한 transfer learning의 가장 큰 수혜를 받는 분야 중 하나이다.
  그러나 이러한 기술들은 적절한 teacher model의 선택과 expensive pre-training을 요구한다.
  최근에는 pretrained teacher에 대한 의존성을 완전히 없애는 연구(예를 들어, 여러 학생 network를 함께 훈련하는 collaborative learning이나 class label을 smooth하게 처리하는 label regularization)가 진행되고 있지만,
  이러한 방법들은 주로 image classification에 초점을 맞추어 왔다.

• traditional transfer learning 및 Knowledge distillation과 달리,
  self-distillation은 동일한 backbone model 내에서 feature extraction 중에 data label로부터 knowledge를 extracting하는 것을 목표로 한다.
  이를 통해 teacher network의 expensive pre-training이 필요하지 않다.
  최근에 개발된 self distillation 방법인 LabelEnc는 object detection에서 label information을 feature map 내에 encoding하여
  내부 neural network layers에서 intermediate supervision을 제공하며,
  COCO dataset에서 이전 작업보다 약 2% 향상된 성능을 달성했다.
  LabelEnc를 기반으로 한 label-guided self-distillation, LGD는 label-과 feature map-encoding을 knolwedge로 활용하여 COCO에서 LabelEnc가 세운 benchmark를 향상시켰다.

• LabelEnc와 LGD는 SOTA를 달성하지만, 간소화된 architectural assumption을 하고 있다.
  첫째, 이들은 Mean Squared Error(MSE)만을 distillation loss로 고려하는데,
  이는 self-distillation setting에서 흔히 발생하는 noisy or imperfect(불완전한) teacher에 대해 robust하지 않다.
  둘째, knowledge distillation coefficient $\lambda$가 전체 loss나 성능에 미치는 영향을 고려하지 않는다.
  이 논문에서는 MSE의 self-distillation loss로서의 limitation과 $\lambda$에 대한 self-distillation의 sensitivity를 탐구할 것이다.
  우리는 Jensen-Shannon(JS) divergence를 결합하고, learning rate에 따라 단계적으로 조정되는 $\lambda$를 사용하는 Smooth and Stepwise Self-Distillation(SSSD)를 제안한다.
  

• 우리의 contribution을 다음과 같이 요악한다 :
  • Smooth and Stepwise Self-Distillation(SSSD) 제안 :
    우리는 stepwise self-distillation을
    smooth, bounded, and symmetric distance인 Jensen-Shannon divergence, JS와 결합한 SSSD를 제안.
    이 distance function, JS는 noise에 robust한 특징을 갖고 있다.
  • knolwedge distillation coefficient $\lambda$의 sensitivity 연구 :
    다양한 architectural assumption 하에서 self-distillation가 distillation coefficient $\lambda$에 어떻게 민감한지 연구하고,
    $\lambda$가 model 성능에 미치는 영향을 연구한다.
  • SSSD의 철저한 benchmarking :
    SSSD를 철저하게 benchmarking하고,
    대부분의 backbone 및 detector network 의 configuration에서
    이전 self-distillation approaches들보다 higher average precision을 달성함을 보여준다.

2. PROPOSED METHOD

2.1. Smooth Self-Distillation

• object detection에서 self-distillation 하는 이전 연구들을 활용하여,
  $P$ scales의 backbone feature pyramid로부터 features들이 얻어진다.

• 우리는 $K \in \{k^p \in \R^{N_p \times M_p}\}^P$를 backbone feature pyramid network로부터 얻은 feature들의 set으로 정의하며,
  여기서 $k^p$는 $p^{th}$ scale의 feature vector이며,
  각 pyramid dimension은 $N_p \times M_p$이고, $p$는 $\{1, ..., P\}$에 속한다.
  
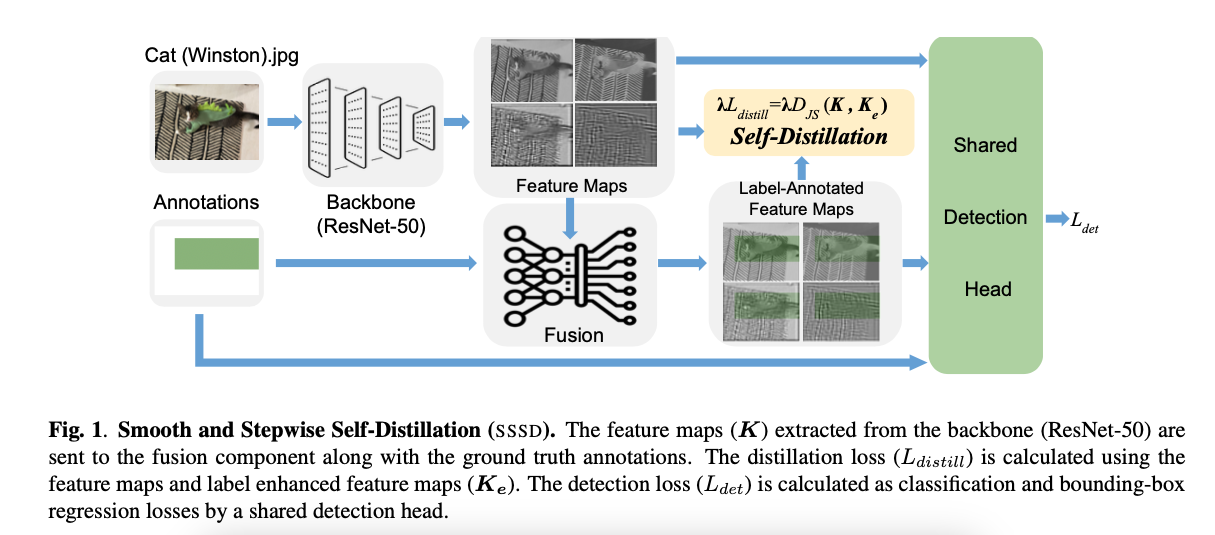
  마찬가지로,
  $K_e \in \{k_e^p \in \R^{N_p \times M_p}\}^P$를 fusion component(Fig. 1)에서 label-annotated된(label로 주석이 달린) feature map($e$)을 통해
  spatial transformer network(STN)으로부터 얻은 feature maps으로 정의한다.
  

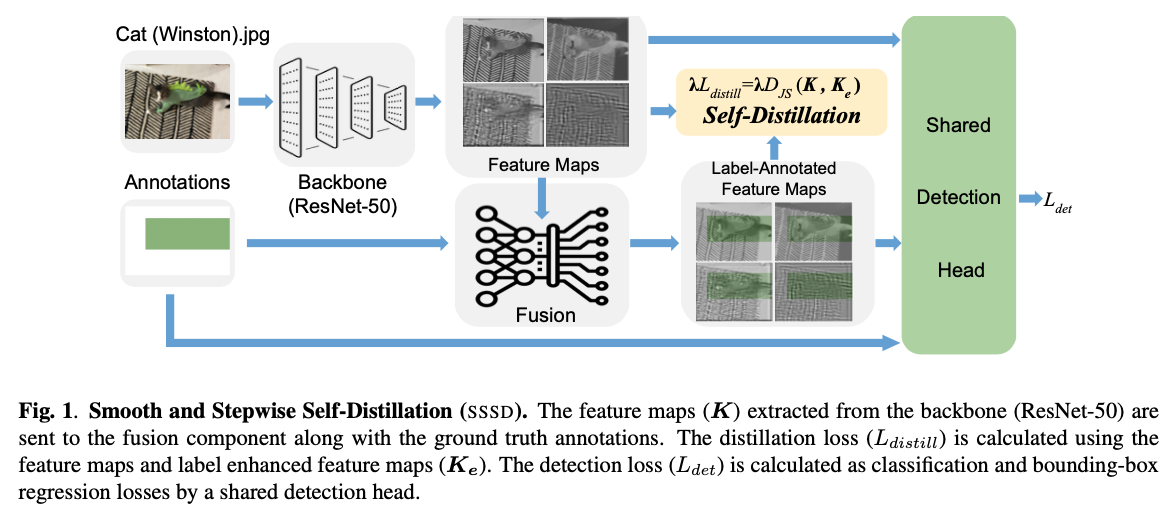
(궁금한 점 : label-annotated feature map은 뭐지?
➡️ 알아본 바에 의하면, label-annotated feature map은 image에 대한 annotation = raw feature representation를 나타냄.
그래서 backbone을 거친 feature map과 label-annotated feature map을 fusion함으로써 명시적으로 labels에 대한 정보를 알려줄 수 있어서
정확하고 effective learning에 효과적으로 사용됨.)

• object detection을 위한 존재하는 self-distillation methods는
  distillation loss를 계산하기 위해 Mean Squared Error(MSE)가 사용된다 :
  
  
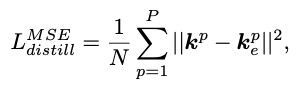
  Kullback-Leibler(KL) divergence도 또한 knowledge distillation을 위해 자주 사용되는 loss function이다.
  
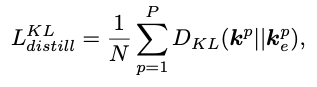
  하지만, KL divergence는 몇가지 limitations이 있다.
  probability distribution $O$와 $Q$에 대해서,
  $D_{KL}(O||Q)$는 bounded되지 않는다면 training 동안에 model divergence(발산)를 유발할 수도 있고,
  low probability를 가진 $O$와 $Q$의 regions에 대해서 민감하다;
  e.g., event $x$에 대해 $O(x) >> Q(x)$일 때 $D_{KL}(O||Q)$는 클 수 있으며,
  이는 $O(x)$가 작더라도 $Q(x)$가 0에 가까울 때 발생할 수 있다.

• 이러한 문제를 해결하기 위해,
  우리는 object detection tasks의 knowledge distillation을 위해 새로운 measure인 Jensen-Shannon(JS) divergence를 사용한다.
  KL divergence와는 달리, JS divergence는 [0, 1]로 bounded되며, symmetric하고 absolute continuity(절대 연속성)을 요구하지 않으며, label noise 및 self-distillation settings에서 흔한 imperfect teachers에도 robust함이 입증되었다.
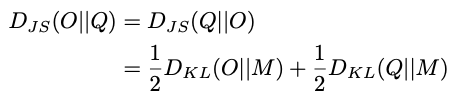
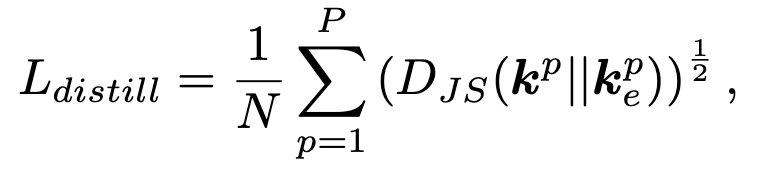
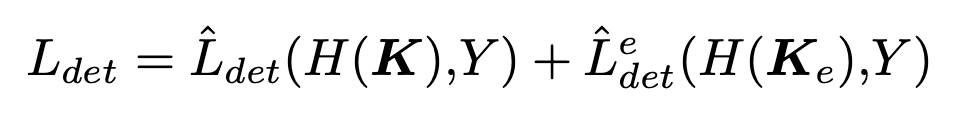
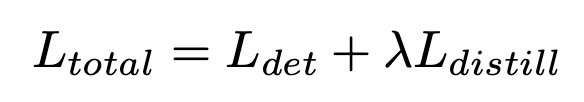  여기서 $\lambda$는 distillation loss에 대한 coefficient를 의미한다.
  $L_{distill}$의 함수 형태를 선택한 이유는 smooth loss functions이 deep neural network training and performance를 향상시킨다는 연구 결과([26, 27])에 의해 motivated되었다.
  JS distance $D_{JS}(O||Q)$는 $D_{KL}(O||Q)$과 $D_{KL}(Q||O)$ 사이의 smooth compromise(타협)으로 간주되기 때문에,
  우리는 이 knowledge distillation method를 smooth self-distillation이라고 부른다.

2.2 Stepwise Self-Distillation

우리는 단계별 자기 증류에서 λ를 λ1과 학습 반복에 따라 달라지는 λ2의 계단 함수로 재정의합니다. 학습률이 120,000번째 반복에서 감소하기 시작하므로, 우리는 λ를 다음과 같이 정의합니다:

• Learning rate scheduling은 training 중 learning rate를 조절하기 위한 중요한 mechanism으로 large scale deep learning에서 널리 사용되며,
  일반적으로 predefined schedule에 따라 learning rate reduction이 이루어진다.
  learning rate decay 중에도 model이 self-distillation로부터 계속 학습할 수 있도록,
  우리는 stepwise self-distillation을 제안하여 learning rate 감소로 인한 감소된 self-distillation loss의 영향을 보완한다.
  우리의 설정에서는 backbone model을 고정시키고 detector를 처음 20k iterations 동안 훈련한다.
  초기 $\lambda$는 경험적으로 처음 20k iterations 이후 distillation loss에 할당된다; 경험적인 $\lambda$ selection은 experimental section에서 자세히 설명됨.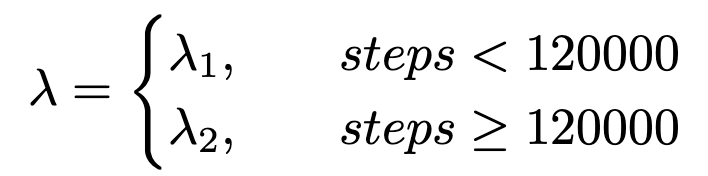

3. Experiments

3.1. Comparisons with SOTA Results

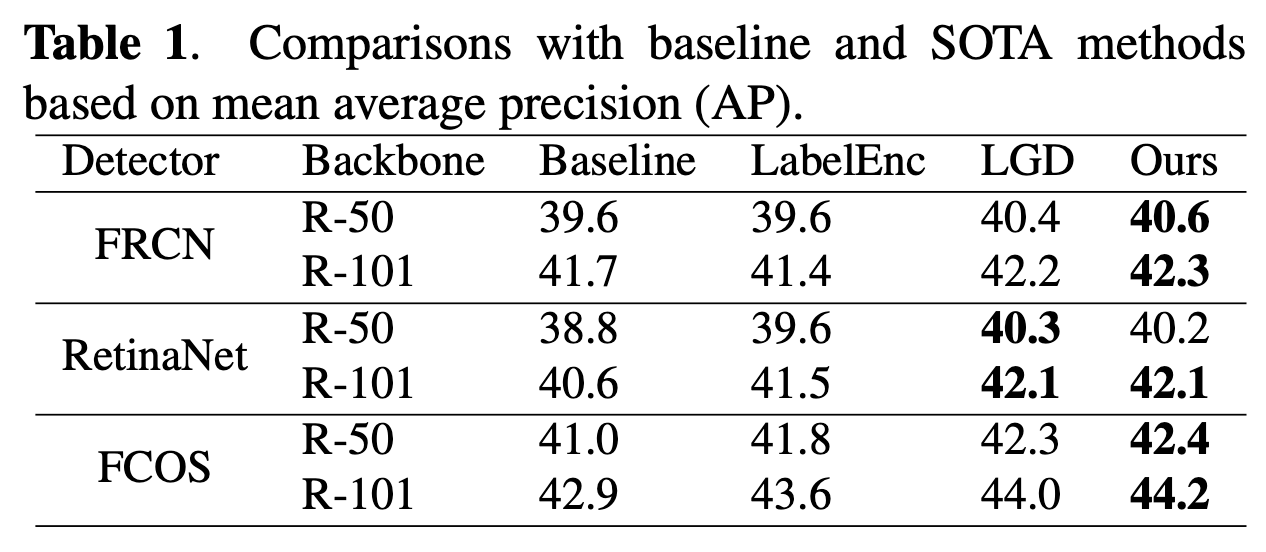
3.2. Effect of Adjusting $\lambda$

• 다음으로,
  우리는 distillation coefficient $\lambda$를 변화시키는 효과를 고려했다.
  이전 연구에서는 $\lambda = 1$을 가정했지만, 우리는 learning rate decay 동안 distillation loss가 overall loss function에 기여하는 정도를 변화시키는 것이 model training에 유익할 수 있다고 추측했다.

• 우리는 LGD와 다른 distillation loss를 사용하고 있기 때문에,
  먼저 LGD와 SSSD 간의 $\lambda$ paramter를 calibrated했다.
  먼저, FRCN detector와 R50 backbone을 사용하여 LGD에서 $\lambda=1$로 설정하여 original experiment를 재현했다; 1,000 iterations 후 penalized distillation loss가 total loss ($\lambda L_{distill}/L_{total}$)에 기여하는 평균 비율은 45%였다.
  우리는 binary search를 이용하여 1,000 반복 후 평균 $\lambda L_{distill}/L_{total} \simeq 0.45$가 되는 [1, 100] 범위 내의 $\lambda$를 계산했으며, SSSD에 대해 동등한 $\lambda$는 50이었다.
  $\lambda$를 조정하는 영향을 탐구하기 위해, 우리는 LGD의 $\lambda \in \{1, 1.5, 2\}$와 SSSD의 $\lambda \in \{50, 75, 100\}$을 고려했다.
  iteration $17 \times 10^4$에서 $\lambda L_{distill}/L_{total}$은 두 architecture에서 유사했다 (Table 3).
  흥미롭게도, 최종 $\lambda L_{distill}/L_{total}$은 $\lambda$에 관계없이 LGD와 SSSD 모두에서 약 50%에 가까웠다.

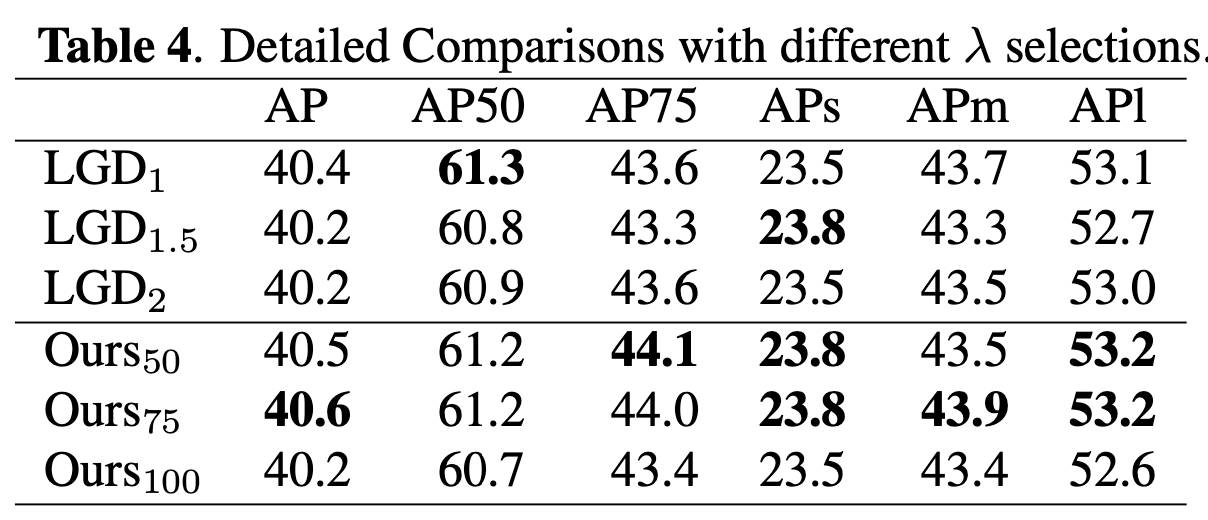
• 우리는 $\lambda L_{distill}/L_{total}$을 비교 가능한 범위로 보정한 후
  LGD와 SSSD의 성능을 비교했다(Fig. 2 및 Table 4).
  SSSD의 최고 성능 $\lambda$(75)는 AP50을 제외한 모든 AP 측정에서 최고 성능 LGD configuration($\lambda=1$)을 일관되게 능가했다.
  모든 $\lambda$를 고려할 때, SSSD는 대부분의 AP variants에서 LGD보다 우수한 성능을 보였으며,
  특히 AP75에서 최대 1.1%(44.1 대 43.6) 향상을 보였다(Table 4).
  또한, 최고 성능 SSSD는 iterations $13 \times 10^4$에서 $17 \times 10^4$까지 LGD보다 우위를 유지했다(Fig. 2).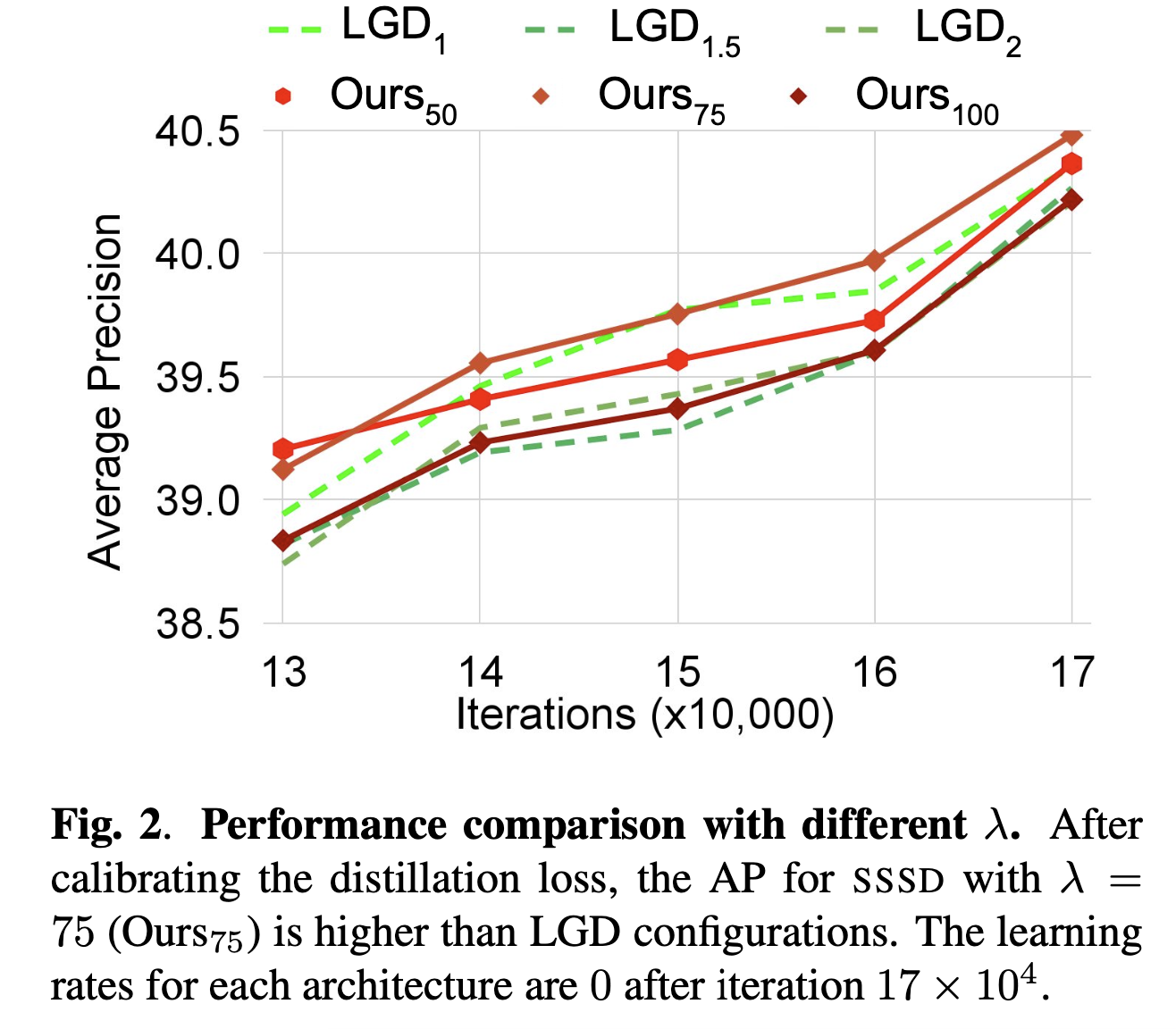

3.3. Stepwise Distillation

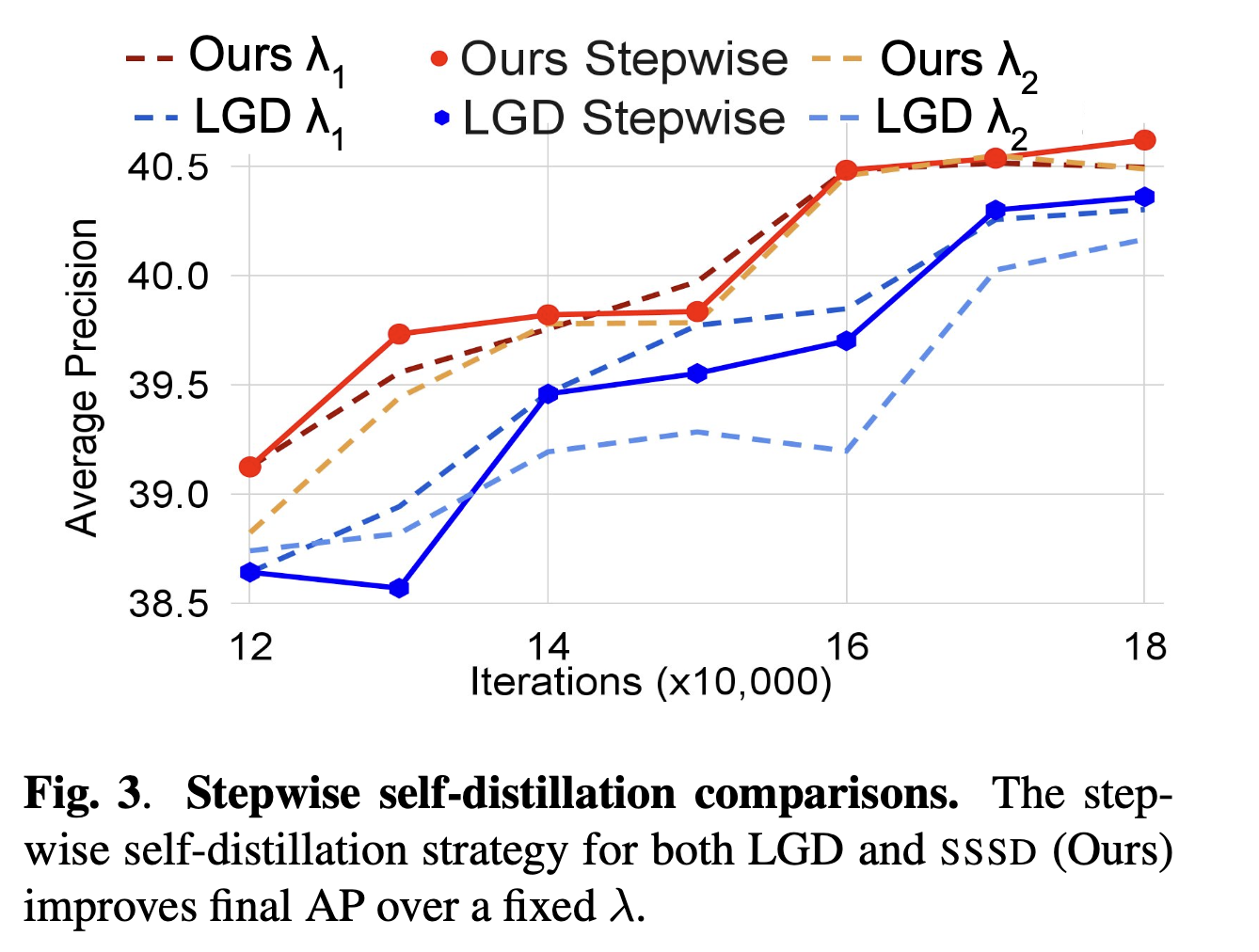
• 마침내,
  우리는 fixed architecture(FRCN-R50)에서 최종 60,000 iteration 동안 LGD와 SSSD에서 stepwise distillation의 효과를 평가했다 (Fig. 3).
  이 architecture에 대해 가장 성능이 좋은 $\lambda$(Table 4)인 LGD $\lambda_1=1$과 SSSD $\lambda_1=75$를 test했다.
  또한, 약간 증가된 값인 LGD $\lambda_2=1.5$과 SSSD $\lambda_2=80$을 test했다.

• 우리는 이러한 고정된 $\lambda$ setting을 iteration 120,000(learning rate scheduler period)에서 $\lambda_1$에서 $\lambda_2$로 전환하는 stepwise distillation와 비교했다.
  stepwise distillation은 고정된 $\lambda$ setting에 비해 LGD와 SSSD 모두에서 약 0.5%의 AP 개선을 보였다(Fig. 3).
  stepwise distillation은 추가적인 computational costs를 부과하지 않으며 architecture와 독립적이기 때문에,
  우리는 stepwise distillation이 다른 knowledge distillation applications에서도 유익할 수 있다고 믿는다.