Paper Info.

https://github.com/JiahuiYu/slimmable_networks

---

이 논문을 읽게 된 이유

• 현재(24.10.28) Object Detection의 Neck에서 width를 줄이는 연구를 하고 있는데,
  다양한 width configuration을 하나의 single network에서 조화롭게 학습시킬 수 있는 방법을 찾고 있는 중이다.

• 참고로, 이 논문의 이전 버전은 Slimmable Neural Networks 이다.

---

Abstract

• Slimmable Networks는 runtime width를 즉시 조절할 수 있는 neural networks family로,
  predefined widths set 중에서 선택하여 runtime에 accuracy-efficiency trade-offs를 optimize하도록 조정할 수 있다.

• 이 연구에서는 universally slimmable networks (US-Nets)을 학습시키기 위한 체계적인 approach를 제안하며,
  slimmable networks를 임의의 width에서도 실행 가능하게 확장하고,
  batch normalization layer가 있는 network와 없는 network 모두에 일반화하였다.

• 또한, US-Nets의 training process를 개선하고 testing accuracy를 높이기 위해 sandwich rule과 inplace distillation이라는 두 가지 improved training techniques을 제안한다.

---

1. Introduction

• slimmable networks가 최근에 소개되어 runtime시 서로 다른 widths로 switch할 수 있으며,
  이를 통해 instant and adaptive accuracy-efficiency trade-offs 조정이 가능하다.
  width는 predefined widths set에서 선택할 수 있으며, 예를 들어 $[0.25, 0.5, 0.75, 1.0]\times$와 같이 설정할 수 있다.
  여기서 $[]\times$는 모든 layer의 width가 전체 model의 0.25로 축소됨을 의미한다.

• slimmable network를 학습시키기 위해 , 각 sub-network에 대한 bn layers를 개별화하는 switchable bn이 제안되었다.
  slimmable network는 같은 width를 갖는 개별 학습된 network와 유사한 accuracy를 가짐.

• slimmable network에서 동기된 또 다른 question은 "can a single neural network run at arbitrary(임의의) width?"이다.
  이 질문은 feature aggregation의 basic form을 rethink하게 했다.
  DNNs에서 a single output neuron은 learnable coefficients로 weighted된 모든 input neurons의 aggregation이다.
  즉, $y = \Sigma^n_{i=1}w_ix_i$에서 $x$는 input neuron, $y$는 output neuron, $w$는 learnable coefficient, $n$은 input channel 개수이다.
  이 공식은 각 input channel 또는 group of channels을 output neurons에 대한 residual component로 볼 수 있다.
  따라서 wider network는 slim network보다 성능이 나쁘지 않아야 한다.
  (slim network의 accuracy는 new connections을 0으로 학습하여 언제든지 달성할 수 있다.)
  즉, single layer를 고려할 때 full aggregation과 partial aggregation 간의 residual error는 감소되며 제한된다 :
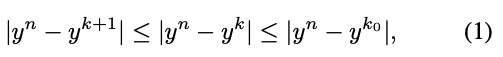  여기서 $y^k$는 처음 $k$개의 channel을 요약한 값이며,
  $y^k = \Sigma^k_{i=1}w_ix_i$, $\forall k \in [k_0, n)$, $k_0$는 constant hyper-parameter이다. (예 : $k_0 = \lceil 0.25n \rceil$)
  이 제한된 inequality(부등식)은 적절하게 학습될 경우, discrete widths set에서 실행가능한 slimmable network가 그 사이의 임의의 width에서도 실행될 수 있음을 시사한다.
  이는 width 증가에 따라 residual error가 감소하고 제한되기 때문이다.
  또한, 이 부등식은 어떠한 BN layer를 사용하더라도 개념적으로 모든 DNN에 적용될 수 있다.
  하지만 [25]에서 제안된 것처럼, BN은 training and testing 간의 inconsistency로 인해 특별한 처리가 필요하다.

• 이 연구에서는 wide range의 임의의 width에서 실행될 수 있는 universally slimmable networks(US-Nets)을 제안한다.
  US-Nets을 training하는 데 세 가지 주요 challenges가 있다.

  1. BN이 포함된 neural networks를 어떻게 처리할 것인가?
     BN은 DL에서 가장 중요한 구성 요소 중 하나이다.
     학습 시, 현재 mini-batch의 mean and variance를 사용하여 feature를 normalize하고, inference 시에는 학습 중에 누적된 moving averaged statistics을 사용한다.
     이 inconsistency는 slimmable networks 학습 실패로 이어진다.
     이후 switchable bn이 도입되었는데, 이 방식은 두 가지 이유로 US-Nets 학습에 실용적이지 않다.
     첫째, 학습 중 모든 sub-networks의 BN 통계를 독립적으로 누적하는 것은 계산 비용이 많이 들고 비효율적이다.
     둘째, 각 iteration에서 sampling된 일부 sub-networks만 update하는 경우, 이 BN 통계가 충분히 누적되지 않아 정확도가 크게 떨어진다.
     이를 해결하기 위해, BN 통계를 학습 후 모든 width에 대해 계산하는 간단한 수정안을 채택했다.
     US-Nets의 weights는 학습 후 고정되므로, 모든 BN 통계를 cluster server에서 병렬로 계산할 수 있다.
     더 중요한 점은, 임의로 sampling된 소수의 학습 image(예 : 1 mini-batch 1024 images)만으로도 이미 정확한 추정이 가능하다는 것이다.
     따라서 BN post-statistics를 매우 빠르게 계산할 수 있다.
     일반화를 위해 BN의 공식 수정이나 새로운 normalization을 제안하지 않았다.
  2. US-Nets을 효율적으로 학습시키려면 어떻게 해야 할까?
     다음으로, Equation 1에 제한된 부등식에서 영감을 받아 US-Nets을 위한 개선된 training algorithm을 제안한다.
     US-Net을 학습하기 위한 자연스러운 방법은 서로 다른 width에서 sampling된 loss를 누적하거나 평균화하는 것이다.
     예를 들어, 각 training iteration에서 $[0.25, 1.0]\times$ 범위에서 $n$개의 width를 무작위로 sampling한다.
     한 걸음 더 나아가, US-Net에서 모든 width의 성능이 가장 작은 폭(예: 0.25×)과 가장 큰 폭(예: 1.0×)의 성능에 의해 제한된다는 점을 주목해야 한다.
     즉, 성능의 lower bound와 uppder bound를 최적화하는 것이 모든 width의 model을 암묵적으로 최적화할 수 있다.
     따라서 $n$개의 width를 무작위로 sampling하는 대신, 각 iteration에서 가장 작은 width, 가장 큰 width, 그리고 $(n-2)$개의 무작위로 sampling된 width에서 model을 학습했다.
     이 규칙을 sandwich rule이라고 부르며 US-Nets을 학습하여 더 좋은 convergence behavior와 overall peformance를 보였다.
  3. individual networks를 학습하는 것과 비교했을 때, US-Nets에서 전체 성능을 향상시키기 위해 무엇을 더 탐구할 수 있을까?
     또한, 한 번의 training iteration에서 a single US-Net 내부에서 full-network에서 sub-network로 knowledge를 전달하는 inplace-distillation을 제안한다.
     이 아이디어는 large model이 먼저 학습되고, 학습된 지식을 soft target prediction으로 small model에 전달하는 two-step knowledge distillation에서 영감을 받았다.
     US-Nets에서는 sandwich rule을 사용하여 model을 가장 큰 width, 가장 작은 width 및 randomly sampled widths된 다른 width로 학습된다.
     이 학습 방식은 inplace knowledge distillation을 자연스럽게 지원한다.
     우리는 가장 큰 width에서의 model prediction을 다른 width에 대한 학습 label로 직접 사용할 수 있고, 가장 큰 width에 대해서는 ground truth를 사용한다.
     이는 추가적인 computation and memory cost 없이 학습 시 inplace로 구현할 수 있다.
     중요한 것은, 제안된 inplace distillation은 일반적이며 image classification뿐만 아니라 image super-resolution and deep reinforcement learning에서도 잘 작동한다는 것이다.

• 제안된 방법을 사용하여 universally slimmable network를 대표적인 과제와 networks(bn 포함 및 미포함, residual network 및 non-residual network 모두)에 적용해 학습했다.
  그 결과, 학습된 US-Nets가 개별적으로 학습된 Model과 유사하거나 더 나은 성능을 보임을 확인했다.
  sandwich rule과 inplace distillation에 대한 광범위한 ablation studies를 통해 제안된 방법의 효과를 입증했다.
  우리의 contributions은 다음과 같다 :

  1. a single neural network를 임의의 width에서 실행 가능하도록 학습할 수 있는 a simple and general approach를 처음으로 제안함.
  2. US-Nets의 학습 과정을 개선하고 test accuracy를 향상시키기 위한 두 가지 개선된 학습 기법을 제안했다.
  3. image classification, image super-resolution 및 reinforcement learning에 대한 실험 및 abaltion study를 제시
  4. US-Nets에 대해 (1) width lower bound $k_0$, (2) width divisor $d$, (3) #sampled widths per training iteration $n$, (4) BN post-statistics을 위한 subset size $s$에 대해 집중적으로 연구.
  5. 모든 layer에 동일하게 적용되는 global width ratio 대신, 각 layer가 자체의 width ratio를 조정할 수 있는 nonuniform US-Nets을 학습하는 데에도 본 방법이 적용 가능함을 보임.
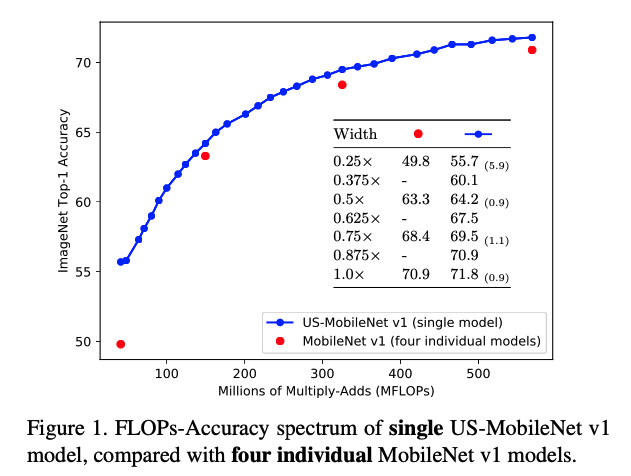
  6. 우리의 발견은 FLOPs-Accuracy spectrum(Fig 1)과 #channels에 대한 one-shot architecture search를 포함한 여러 관련 분야로의 가능성을 확장함.
     

---

2. Related Work

Slimmable Network

• [25]는 runtime 시 다양한 widths에서 실행 가능한 a single neural network를 학습하는 초기 approach를 제안했다.
  이 방법은 instant and adaptive accuracy-efficiency trade-offs를 가능하게 하며, width는 predefined widths set에서 선택할 수 있다.
  slimmable network 학습의 주요 장애물은 channel 수가 다를 때 다른 feature의 mean and variance가 발생한다는 것이다.
  이러한 차이는 서로 다른 sub networks 간의 불일치를 초래하여, shared BN layers의 통계가 부정확해진다.
  이를 해결하기 위해 slimmable network 내의 각 sub-networks에 독립적인 BN을 적용하는 Switchable BN이 제안되었다.

---

3. Universally Slimmable Networks

3.1. Rethinking Feature Aggregation

• DNNs은 각 layer가 neuron으로 구성된 layer로 이루어져 있다.
  DL의 기본 요소인 neuron은 모든 input neuron의 weighted sum을 수행하여 값을 계산하고, layer를 거쳐 최종 prediction을 만든다.
  예는 Figure 2.에 나와 있다.
  출력 neuron $y$는 다음과 같이 계산된다 :
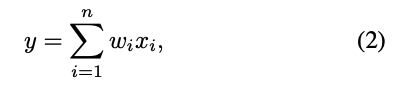  여기서 $n$은 input neuron(또는 CNNs의 channels)의 수, $x = \{x_1, x_2, …, x_n\}$는 input neuron, $w = \{w_1, w_2, …, w_n\}$은 learnable coefficient, $y$는 single output neuron이다.
  이 과정은 feature aggregation으로도 알려져 있다.
  각 input neuron은 특정 feature를 감지하고, output neuron은 learnable transformations을 통해 모든 input feature를 aggregate한다.
  network의 channel 수는 보통 수동으로 선택된 hyperparameter(예 : 128, 256, ..., 2048)이다.
  이는 deep models의 accuracy와 efficiency에 중요한 역할을 하며, 일반적으로 더 wider network는 더 높은 accuracy를 제공하지만 runtime efficiency가 떨어진다.
  flexibility를 제공하기 위해, 많은 architecture engineering 연구는 서로 다른 width multipliers를 사용하여 제안된 network를 각각 학습한다.
  여기서 width multipliers는 network의 각 layer를 uniformly하게 줄이는 global hyper-parameter이다.

• 우리는 임의의 width에서 직접 실행시킬 수 있는 a single network를 학습시키는 것을 목표로 한다.
  Figure 2에 보이듯이, feature aggregation은 channel-wise residual learning의 관점에서 명시적으로 해석될 수 있으며,
  각 input channel 또는 channel group을 output neuron의 residual componenet로 간주할 수 있다.
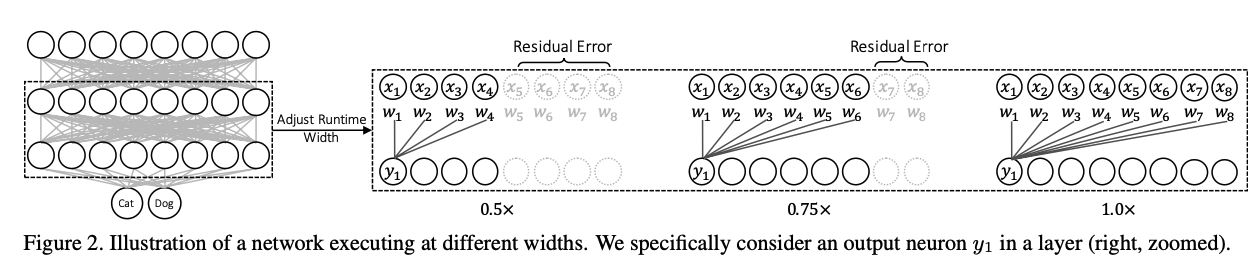  따라서 wider network는 그보다 slim network보다 성능이 나빠지지 않는다.
  다시 말해, fully aggregated feature $y_n$과 partially aggregated feature $y_k$ 간의 residual error $\delta$는 감소하고 경계가 생긴다 :
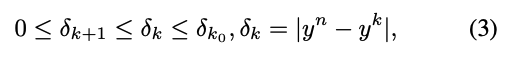  여기서 $y_k$는 첫 $k$개의 channel을 요약한 값 $y^k = \sum_{i=1}^k w_i x_i$이며,
  $\forall k \in [k_0, n)$ 이고 $k_0$ 는 constant hyper-parameter이다. (예: $k_0 = \lceil 0.25n \rceil$).
  Equation 3의 bounded inequality(경계 부등식)은 몇 가지 단서를 제공한다 :

  1. 특정 width set에서 실행할 수 있는 slim network는 학습이 적절히 이루어졌다면 그 사이의 모든 width에서 실행될 수 있다.
     즉, a single neural network는 $k$가 $k_0$에서 $n$까지의 넓은 범위에서 어떤 width에서도 실행될 수 있다.
     이는 각 feature의 residual error가 $\delta_{k_0}$로 정해져 있고 width $k$가 증가할수록 감소하기 때문이다.
  2. 개념적으로 이 bounded inequality는 어떤 normalization layer(예 : bn and weight normalization)을 사용하든 모든 deep neural network에 적용된다.
     따라서 다음 section에서는 임의의 width에서 실행 가능한 single neural network를 학습하는 방법을 주로 탐구한다.
     이러한 network를 universally slimmable networks, 간단히 US-Nets라고 부른다.

3.2. Post-Statistics of Batch Normalization

• 하지만, [25]에서 제시된 것 처럼, BN은 training 과 testing 사이의 inconsistency로 인해 특별한 처리를 해줘야 한다.
  training 동안, 각 layer의 features들은 현재 mini-batch feature values $x_B$의 mean and variance로 normalized된다 :
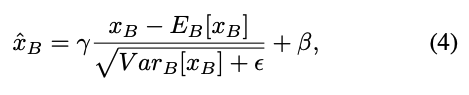  $\epsilon$은 zero-division을 피하기 위한 a small value (e.g. $10^{-5}$)이고,
  $\gamma$와 $\beta$는 각각 learnable scale and bias이다.
  그리고나서 feature mean and variance 값은 moving averages로서 global statistic로 update된다 :
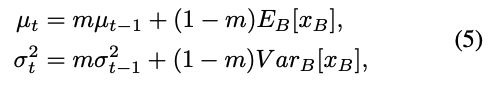  $m$은 momentum (e.g. $0.9$), $t$는 the index of training iteration이다.
  우리는 network가 총 $T$ iteration 동안 학습된다고 가정하며, $\mu = \mu_T, \sigma^2 = \sigma^2_T$로 표시한다.
  inference 중에는 다음과 같은 global statistics가 사용된다 :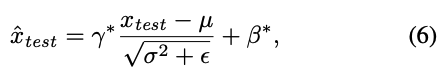 $\gamma^*$와 $\beta^*$는 optimized된 scale and bias이다.
  training 이후에는, Equation 6은 a simple linear transformation으로 재정의된다는 것을 명심해라 :
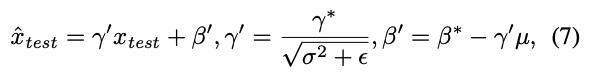  그리고 일반적으로 $\gamma{\prime}$와 $\beta{\prime}$는 이전의 conv layer에 fused될 수 있다.

• slimmable networks에서는, 서로 다른 channel 수를 축적하면서도 서로 다른 feature mean and variance가 발생하여 공유된 BN의 통계가 부정확해진다.
  [25]에서는 각 sub-networks에 대해 BN의 $\gamma, \beta, \mu, \sigma^2$를 개별적으로 사용하도록 하는 switchable BN을 도입했다.
  학습 후에는 $\gamma, \beta$ parameter가 합쳐질 수 있지만(Eq 7), 공유된 $\gamma, \beta$를 사용하는 slimmable network도 유사한 성능을 보인다.
  그러나 universally slimmable network에서는 switchable BN이 실용적이지 않다.
  그 이유는 두 가지이다.

  1. US-Net의 모든 sub-networks의 독립적인 BN 통계를 학습 중에 축적하는 것은 계산량이 많고 비효율적이다.
  2. 매 iteration에서 일부 sampled sub-networks만 update할 경우, BN 통계가 충분히 축적되지 않아 부정확해지며, 이는 실험에서 accuracy가 크게 떨어지는 결과를 초래한다.
     
     이를 해결하기 위해, 문제를 적절히 해결할 수 있는 간단한 수정으로 BN을 조정했다.
     이 수정은 학습 후 모든 width의 BN 통계를 계산하는 것이다.
     US-Net의 learnable parameter가 고정되면, 모든 BN 통계를 cluster server에서 parallel로 계산할 수 있다.
     학습 중에는 training sample을 통해 BN 통계를 계산할 수 있으며, 이는 Equation 5의 moving averages 또는 아래와 같은 정확한 average로 계산된다:
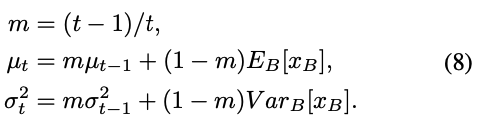     실험 결과, exact averages가 moving averages보다 약간 더 나은 성능을 보였다.

• 실제로, 모든 training samples에 대해 BN 통계를 축적할 필요는 없으며, 무작위로 sampled된 subset(e.g. 1$k$ images)만으로도 정확한 esimation을 제공한다.
  이 option을 통해 BN의 post-statistics 계산을 매우 빠르게 수행할 수 있다(default는 모든 training sample에 대해 계산)
  실험에서는 sample sizes별 정확도를 비교할 예정임.
  또한, 연구나 개발 과정에서 model의 학습 중 validation accuracy를 추적하는 것이 중요하다.
  BN의 post-statistics는 학습 중 validation accuracy 추적을 지원하지 않지만, US-Net을 학습할 때 간단한 engineering trick을 사용할 수 있다.
  학습 중 largest and smallest width에서 BN statistics을 추적하는 방법이다.

---

4. Improved Training Techniques

• 이 section에서는 US-net의 training algorithm을 from bottom to top까지 설명한다.
  먼저 sandwich rule과 inplace distillation 방식의 동기와 세부 사항을 소개한 후, US-Nets 학습을 위한 overall algorithm을 제시한다.

4.1. The Sandwich Rule

• US-Net을 학습하기 위한 자연스러운 solution은 서로 다른 sub-networks에서 sampling한 loss를 누적하거나 평균화하는 것이다.
  예를 들어, 각 training iteration에서 $[0.25, 1.0]\times$ 범위에서 $n$개의 width를 무작위로 sampling하고,
  누적된 loss로부터 back-propagated된 gradients를 적용할 수 있다.
  한 단계 더 나아가, Eq 3의 bounded inequality를 통해 US-Net의 모든 width에서 성능이 최소 width 0.25x와 최대 width 1.0x에서 model의 성능에 의해 제한됨을 알 수 있다.
  즉, 성능의 하한과 상한을 최적화하면 US-Net의 모든 sub-networks를 암묵적으로 최적화할 수 있다.
  따라서 각 iteration에서 model을 최소 width, 최대 width, $(n-2)$개의 무작위 width로 학습하는 sandwich rule을 제안하며, 이를 통해 더 나은 convergence behavior와 overall performance를 실험에서 확인하였음.

• sandwich rule은 두 가지 추가적인 이점을 제공한다.

  1. secion 3.2에서 언급한 것처럼, 최소 width와 최대 width를 학습함으로써 학습 중 model의 validation accuracy를 명확하게 추적할 수 있으며, 이는 또한 US-Net의 성능 하한과 상한을 나타낸다.
  2. 최대 width를 학습하는 것은 다음 학습 기법인 inplace distillation을 위해서도 중요하고 필수적이다.

4.2. Inplace Disillation

• Inplace distillation의 핵심 아이디어는 각 iteration마다 동일 network 내에서 전체 network에서 sub-network로 knowledge를 전달하는 것이다.
  이는 먼저 큰 model을 학습한 후 학습된 knowledge를 예측된 class soft probability를 사용하여 작은 model로 전이하는 two-step knowledge distilling에서 영감을 받았다.
  US-Net에서는 sandwich rule에 따라 각 iteration마다 최대 width, 최소 width 및 무작위로 sampling한 width로 model을 학습한다.
  주목할 점은 이 학습 방식이 inplace distillation을 자연스럽게 지원한다는 것이다.
  최대 width에서 model이 예측한 label들을 다른 width의 학습 label로 직접 사용하며, 최대 width에서는 ground truth를 사용한다.

• 구체적으로, 최대 width에서 예측된 label tensor의 gradient를 멈추는 것이 중요하다.
  이는 sub-network의 loss가 전체 network의 computation graph를 통해 back-propagate되지 않음을 의미한다.
  또한, BN을 사용할 경우 예측된 label은 training mode에서 직접 계산되며, 이는 inference mode의 추가 forward cost를 절감해준다.
  우리는 sub-networks의 training label로 ground truth label과 predicted label을 함께 사용하는 방식을 시도해봤으며,
  두 loss의 일정한 balance 또는 감소하는 balance를 사용하는 경우를 test했으나 결과는 오히려 좋지 않았다.

4.3. Training Universally Slimmable Networks

• sandwich rule과 inplace distillation을 적용하여, US-Net을 학습하는 전체 algorithm이 algorithm 1에 제시되어 있다.
  간단히 하기 위해, BN의 post-statistics을 계산하는 식(Eq 8)은 포함하지 않았다.
  다음의 사항들을 주목해야 한다:
  (1) 이 algorithm은 다양한 작업과 network에 일반적으로 적용 가능하다.
  (2) GPU memory cost은 individual networks를 학습할 때와 동일하므로 동일한 batch size를 사용할 수 있다.
  (3) 모든 실험에서 동일한 hyper-parameters가 적용되었다.
  (4) 구현이 비교적 간단하며, Algorithm 1에서 PyTorch-Style pseudo code로 예시를 제공한다.
  

---

요약

최대 width network를 inference : y'
randomly sampled network들과 최소 width network를 inference : loss()

optimizer.zero_grad()

	y_max = model.forward(max_width)
	loss_max = criterion(y_max, y)
	loss_max.backward()
	y_max = y_max.detach()
	
	y_randomly_sampled_1 = model.forward(randomly_sampled_1)
	loss_1 = distill(y_randomly_sampled_1, y_max)
	loss_1.backward()
	
	y_randomly_sampled_2 = model.forward(randomly_sampled_2)
	loss_2 = distill(y_randomly_sampled_2, y_max)
	loss_2.backward()
	
	y_min = model.forward(min_width)
	loss_min = criterion(y_min, y)
	loss_min.backward()

optimizer.step()

training end -----------------------------------------------------------

bn_calibration_init() # calculating post-statistics of batch normalizations