Paper Info

JMLR 2022

---

Abstract

• DL에서, model은 일반적으로 모든 inputs에 same parameters를 사용한다.
  하지만 MoEs models은 이를 따르지 않고 각 example에 대해 different parameters를 선택한다.
  그 결과, outrageous number of(매우 많은) params을 가진 sparsely-activated model이 탄생했지만, a constant computational cost(비용은 일정하게 유지된다).
  하지만 MoE의 몇 가지 주목할 만한 성공에도 불구하고, complexity, communication costs, and training instability로 인해 widespread adoption되지는 못했다.

• 이 문제를 해결하기 위해 Switch Transformer를 도입했다.
  우리는 MoE routing algorithm을 단순화하고 communication and computational costs를 줄이면서 직관적으로 개선된 models을 설계했다.
  our proposed training technique은 instabilities를 완화하며,
  large sparse models을 처음으로 lower precision (bfloat16) formats으로 train할 수 있음을 보여준다.

• T5-Base와 T5-Large를 기반으로 한 model을 설계하여 동일한 computational resources로 pre-training speed를 최대 7x까지 향상시켰다.
  이러한 improvements는 multilingual(다국어) settings으로도 확장되어 101개 언어에서 mT5-Base version 대비 성능 향상을 측정했다.

• 마지막으로, 우리는 trillion parameter models을 가진 language models을
  "Colossal Clean Crawled Corpus"에서 pre-training하며
  현재 language models의 scale을 확장했다.
  또한 T5-XXL model 대비 4x speedup을 달성했다.

---

1. Introduction

• Large scale training은 flexible and powerful neural language models로 가는 effective path로 입증되어왔다.
  model scale의 성공에 영감을 얻었지만 더 greater computational efficiency를 추구하기 위해,
  우리는 sparsely-activated expert model: the Switch Transformer를 제안한다.
  이 model의 sparsity는 each incoming example에 대해 a subset of the nueral network weights만 activating함으로써 발생한다.

• sparse training은 research and engineering에서 active area이지만, ML libraries and HW accelerators가 여전히 dense matrix multiplications에 적합하게 설계되어 있다.
  efficient sparse algorithm을 위해, 우리는 MoE paradigm을 시작점으로 삼아 training instabilities와 computational benefits을 제공하는 단순화된 model을 설계했다.
  MoE model은 notable successes in machine translation을 보여줬지만, complexity, communication costs, and training instabilities로 인해 널리 적용되지는 못했다.

• 우리는 이러한 문제를 해결했을 뿐만 아니라, translation을 넘어서, NLP에서도 these class of algorithms이 유용하다는 것을 발견했다.
  이 연구는 주로 model의 scale(확장성)에 초점을 맞췄지만, Switch Transformer architecture가 supercomputers뿐만 아니라 only a few computational cores에서도 유용하다는 것을 보여준다.
  또한 우리의 sparse models은 small dense versions로 distilled될 수 있으며, sparse model의 quality gain의 30%를 유지할 수 있다.

• Our contributions are the following:

  • The Switch Transformer architecture는 MoEs를 simplifies and improves했다.
  • stronly tuend T5 model과 비교하여 7x pre-training speedups하면서도 token당 동일한 FLOPs 사용.
    또한, limited computational resources에서도 성능 개선.
  • Successful distillation of sparse pre-trained and specialized fine-tuned models into small dense models.
    model size를 최대 99% 줄이면서도 quality gains의 30%를 유지.
  • Improved pre-training and fine-tuning techniques:
    1. bfloat16과 같이 lower precision으로도 training할 수 있는 selective precision training
    2. 더 많은 experts수로 확장할 수 있는 an initialization scheme
    3. sparse model fine-tuning and multi-task training을 향상시킬 수 있는 increased expert regularization
  • multilingual(다국어) data에서 pre-training benefits 측정.
    91% 언어에서 mT5 baseline 대비 4x+ speedups
  • data, model, and expert-paralleism을 효율적으로 결합하여 최대 a trillion params를 가진 model 생성.
    stronly tuned T5-XXL baseline 대비 pre-trainiend speed를 4x 향상.
    

---

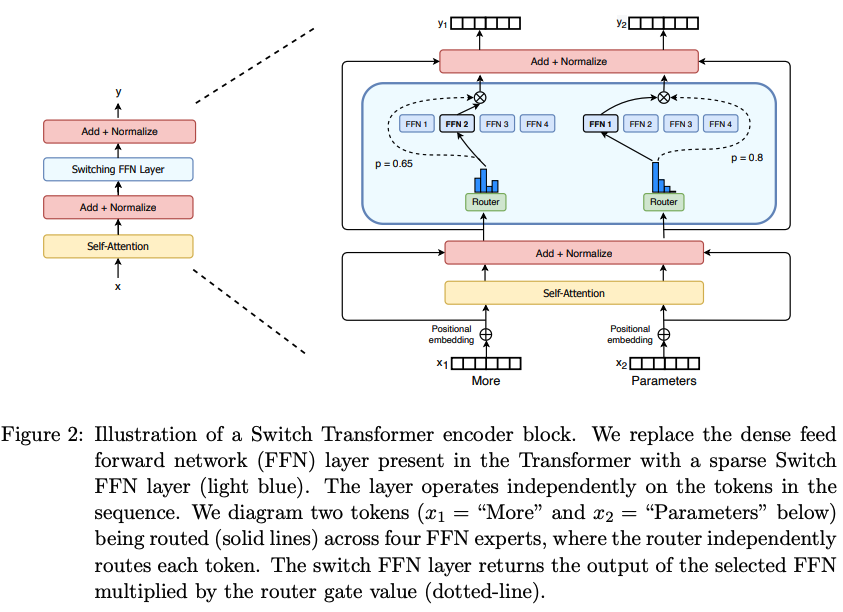
2. Switch Transformer

• Switch Transformer의 design principle(원칙)은 Transformer model의 #params를 maximize하면서도
  a simple and computationally efficinet way를 추구하는 것이다.
  model scale의 이점은 Kaplan et al. (2020)에서 철저히 연구되었으며,
  model size, data set size and computational budget 사이에 uncovered power-law scaling(멱법칙? 위키백과: 은 한 수가 다른 수의 거듭제곱으로 표현되는 두 수의 함수적 관계를 의미. 예를 들어, 특정 인구수를 가지는 도시들의 숫자는 인구수의 거듭제곱에 반비례하여 나타남) 관계가 있음을 밝혀냈다.
  특히, 이 연구는 상대적으로 small amount of data로 large models을 training하는 것이 계산적으로 optimal approach라고 주장한다.

• 이 결과를 바탕으로, 우리는 네번째 axis를 조사한다:
  example당 FLOPs를 constant(일정하게) 유지하면서 #params를 증가시키는 것이다.
  우리의 가설은, total computation과 독립적으로 #params 자체가 확장가능한 또 다른 중요한 axis라는 것이다.
  이를 위해 우리는 GPUs와 TPUs와 같은 dense matrix multiplications에 최적화된 HW를 효율적으로 사용할 수 있는 a sparsely activated model을 설계했다.
  이번 연구에서는 TPU architectures에 초점을 맞췄지만, 이 class의 models은 GPU clusters에서도 유사하게 학습할 수 있습니다.
  distributed training setup에서 우리의 sparsely activated layers는 unique(고유한) weights를 서로 다른 devices에 분할한다.
  따라서 model의 weights 수는 devices 수와 함께 증가하지만, 각 device에서 memory와 computational footprint는 manageable 수준으로 유지된다.

2.1 Simplifying Sparse Routing

Mixture of Expert Routing.

• Shazeer et al. (2017)은
  token representation $x$을 입력으로 받아,
  해당 layer에 있는 $N$개의 experts 집합 $\{E_i(x)\}^N_{i=1}$ 중에서 best top-$k$ experts를 결정하여 routing하는
  natural language MoE layer를 제안했다.

• router variable $W_r$는 logits $h(x) = W_r x$ 를 생성하며,
  이는 해당 layer의 $N$개의 experts에 대해 softmax distribution으로 normalized된다.
  특정 expert $i$의 gate-value는 다음과 같이 주어진다:
  token $x$의 routing을 위해 top-$k$ gate values가 선택된다.
  만약 $T$가 선택된 top-$k$ indices 집합이라면, layer의 output computation은
  각 expert의 token에 대한 계산을 gate value로 linearly weighted를 적용한 combination으로 표현된다:
  

Switch Routing: Rethinking Mixture-of-Experts.

• Shazeer et al. (2017)은 $k > 1$ experts로 routing하는 것이 routing functions에 non-trivial한 gradient를 제공하는 데 필수적이라고 conjectured(추측)했다.
  (적어도 두 개 이상의 experts에 routing해야 한다)
  저자들은 적어도 두 expert를 비교하지 않으면 routing 학습이 제대로 작동하지 않을 것이라고 intuited(직관)했다.

• 이러한 ideas와 달리, 우리는 only a single expert로만 routing하는 a simplifed strategy를 사용한다.
  우리는 이 simplification이 model quality를 유지하면서 routing computation을 줄이고 성능을 향상시킬 수 있음을 보였다.
  이 $k=1$ routing strategy는 이후 Switch layer로 언급된다.
  MoE와 Switch Routing 모두에서, Equation 2의 gate value $p_i(x)$는 router의 differentiability를 허용한다는 점에 유의해라.

• Switch layer의 benefits은 세 가지로 요약된다:

  1. token을 a single expert에게만 routing하기 때문에 router computation이 줄어든다
  2. 각 expert의 batch size (expert capacity)가 최소 절반으로 감소할 수 있다.
     이는 각 token이 single expert로만 routing되기 때문이다.
  3. routing implementation이 단순화되고 communication costs가 감소된다.

2.2 Efficient Sparse Routing

• 우리는 Mesh-TensorFlow(MTF)를 사용했다.
  MTF는 physical set of cores를 logical mesh of processors로 추상화하여
  efficient distributed data and model parallel architectures를 지원한다.
  우리는 statically declared sizes를 선언해야 하는 TPU를 염두에 두고 model을 설계했다.

• 아래는 our distributed Switch Transformer에 대해 설명할 것이다.

Distributed Switch Implementation

• 우리의 tensor shapes은 모두 compilation time에 정적으로 결정되지만,
  training 및 inference 시 routing decisions으로 인해 연산은 dynamic하게 이루어진다.
  이 때문에 중요한 기술적 고려사항 중 하나는 expert capacity를 설정하는 방법이다.
  expert capacity, 즉 expert가 처리하는 #tokens는 batch 내 #tokens을 #experts로 evenly(균등하게) 나눈 다음,
  이를 capacity factor로 확장하여 설정한다.
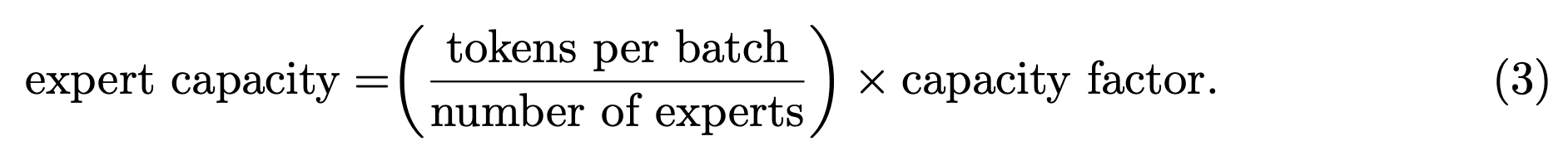  capacity factor가 1.0보다 크면, token이 experts 간에 완벽하게 균등하지 않게 분배되는 상황을 대비하기 위한 추가의 buffer가 생성된다.
  하지만 너무 많은 Tokens이 한 expert에게 routing되는 경우(이후 dropped tokens이라고 부름),
  해당 tokens은 연산이 생략되고 residual connection을 통해 다음 layer로 직접 전달된다.

• 그러나 expert capacity를 증가시키는 데도 drawbacks이 있다.
  capacity가 너무 크면 computation and memory가 낭비되기 때문이다.
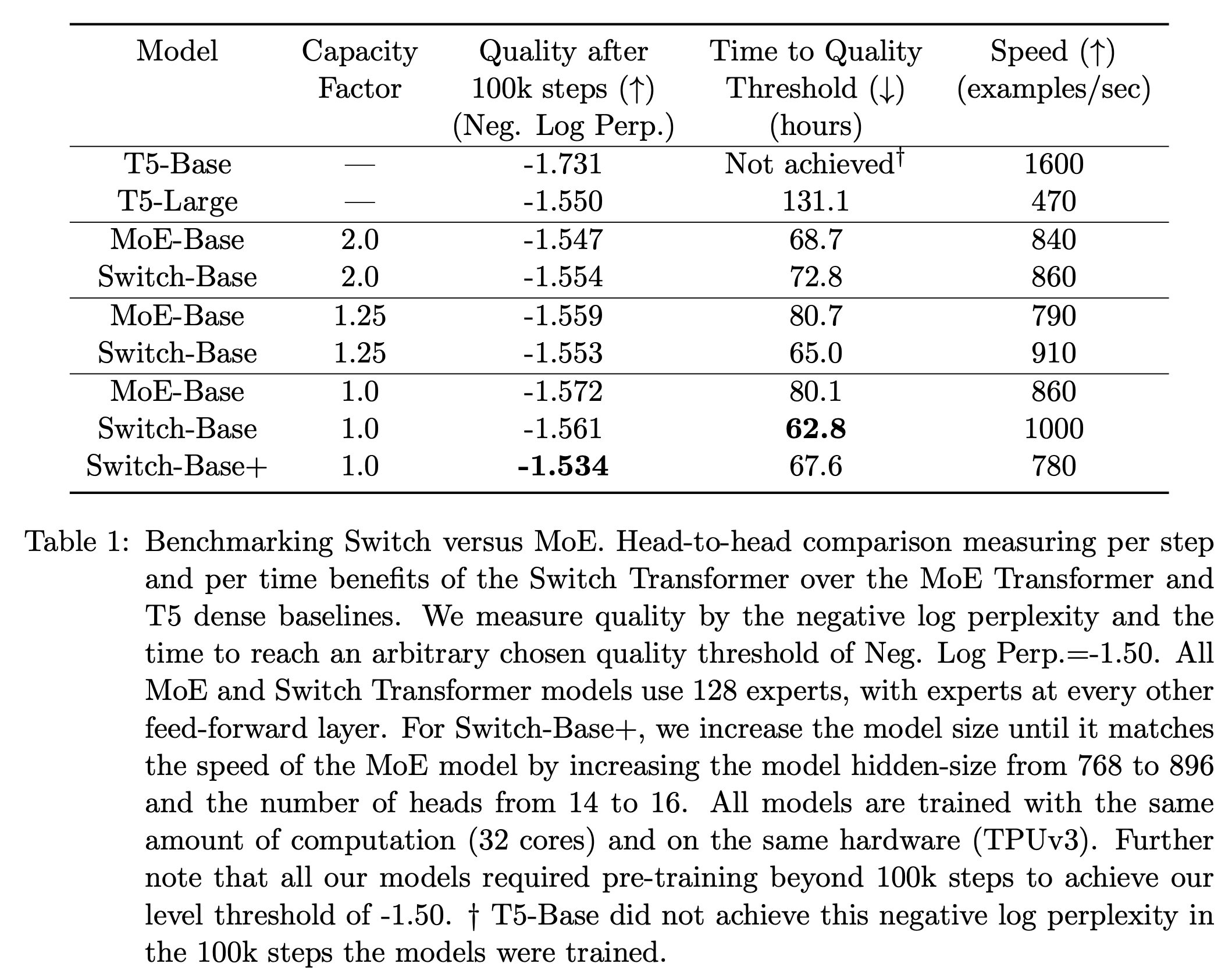
  이 trade-off는 Figure 3에서 설명된다.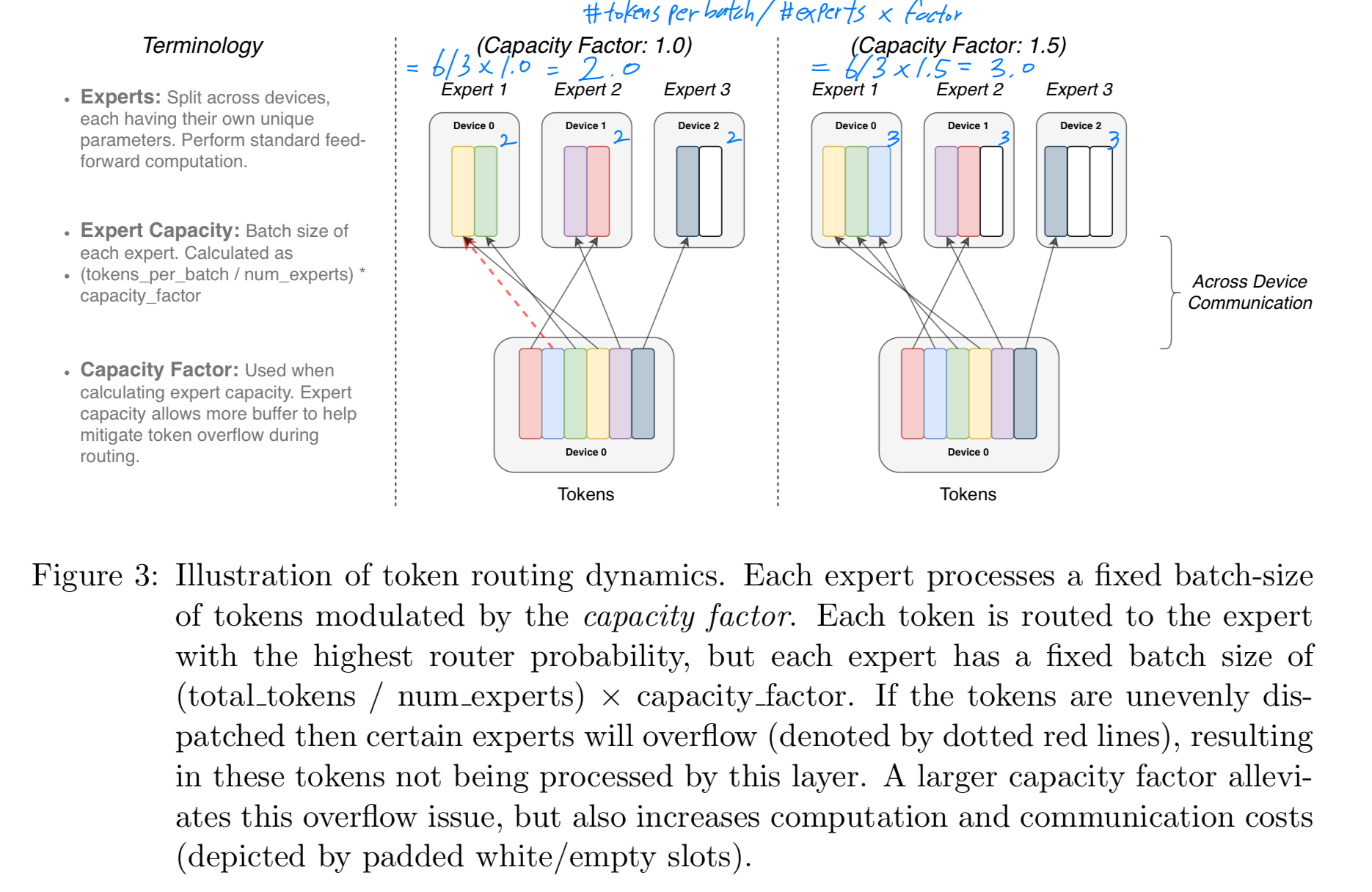실험적으로 우리는 dropped tokens의 비율을 낮게 유지하는 것이 sparse expert models의 확장성에 중요하다는 것을 발견했다.
  (token들이 expert에 균등하게 routing되는 것이 expert models의 확장성에 중요하다)
  실험 전반에 걸쳐 dropped token의 수는 expert 수에 의존하지 않는 것으로 나타났다.(일반적으로 < 1%)
  충분히 높은 coefficient(계수)를 가진 auxiliary load balancing loss를 사용하면 Load balancing이 잘 이루어졌다.
  이러한 design decisions이 model quality and speed에 미치는 영향은 Table 1에서 다룬다.
  

A Differentiable Load Balancing Loss

• experts들 사이에 balanced loss를 encourage하기 위해 우리는 an auxiliary loss를 추가했다.
  Shazeer et al. (2018); Lepikhin et al. (2020)에서 처럼,
  Switch Transformers Shazeer et al. (2017)의 original design을 단순화했다.
  original design에는 Load-balancing loss와 importance-weighting loss가 별도로 존재했지만, Switch Transformers에서는 이를 단순화했다.

• 각 Switch layer에 대해서, 이 auxiliary loss는 학습 시 전체 model loss에 추가된다.
  $i=1$ to $N$까지 indexing된 $N$개의 experts와 $T$개 tokens을 갖는 a batch $B$가 주어졌을 때,
  auxiliary loss는 vectors $f$와 $P$ 사이의 scaled dot-product로 계산된다.
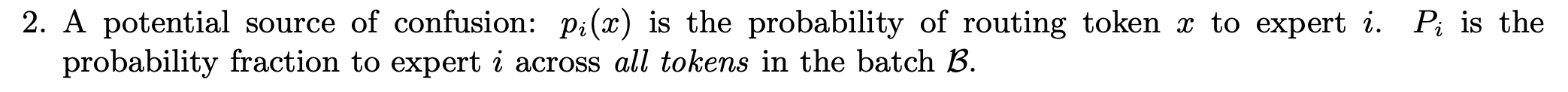  $f_i$는 expert $i$에 할당된 tokens의 비율을 나타내며,
  $P_i$는 batch $B$ 내 모든 tokens에 대한 expert $i$에 할당된 router probability의 비율을 나타낸다.
  token batch를 $N$개의 experts에 균등하게 routing하기 위해, 두 vector($f$, $P$) 모두 값이 $1/N$이 되기를 기대한다.
  Eq 4의 auxiliary loss는 uniform distribution에서 minimized되므로 uniform routing을 유도한다.
  이 objective는 $P$-vector가 differentiable하므로 differentiated하지만, $f$-vector는 differentiable하지 않다.
  final loss는 expert 수 $N$으로 곱하여, expert 수가 변하더라도 loss가 일정하게 유지되도록 한다.
  이는 uniform routing에서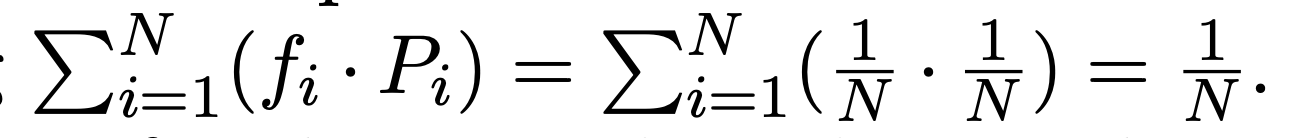을 만족하기 때문이다.
  마지막으로 hyperparameter $\alpha$는 이러한 auxiliary losses를 위한 multiplicative coefficient이다.
  본 연구에서는 $\alpha=10^{-2}$을 사용했으며, 이는 load balancing을 충분히 보장하면서 primary cross-entropy objective를 방해하지 않을 정도로 작았다.

2.3 Putting It All Together: The Switch Transformer

• Switch Transformer의 첫 test는 "Colossal Clean Crawled Corpus"에서 pre-training을 시작으로 진행되었다.
  pre-training objective는 masked language modeling task를 사용하여, missing tokens을 predict하도록 했다.