1. 차원 축소
1-1. 차원의 저주 (Curse of Dimensionality)
차원의 저주란 데이터의 차원이 증가할수록 공간의 부피가 기하급수적으로 커져서, 기존에 효과적이던 알고리즘이나 분석 방법들이 성능이 급격히 떨어지는 현상을 말한다.
고차원에서는 데이터가 희소하게 분포되며, 거리 기반 알고리즘(예: KNN, 클러스터링 등)은 모든 점 사이의 거리가 비슷해지는 문제를 겪게 되고, 학습에 필요한 데이터 양도 급격히 증가한다.
따라서 차원이 너무 높아지면 오히려 예측 정확도나 일반화 성능이 나빠질 수 있어서 이를 해결하기 위해 차원 축소 기법(PCA, t-SNE 등)이 자주 사용된다.
이렇게 낮은 차원에서는 멀리 떨어져 있던 것이, 고차원에서는 가까이 위치하게 된다.
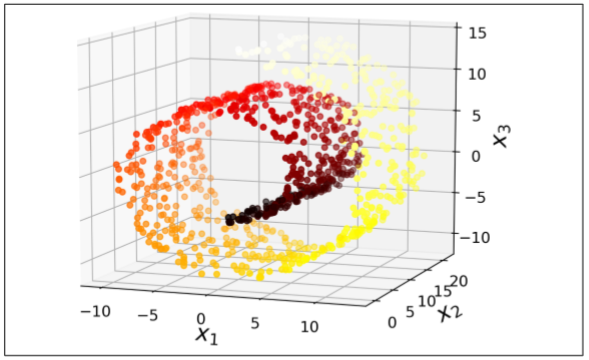
위에는 고차원에서 롤케이크처럼 둘둘 말려서 낮은 차원에서는 멀리 떨어져 있던 것이 가까워지는 모습이다.
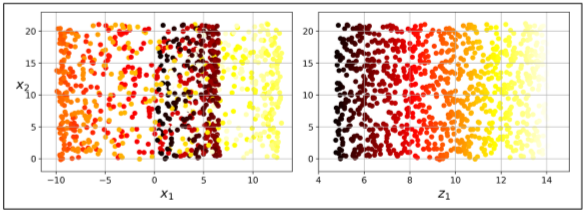
1-2. 차원 축소 (Dimensionality Reduction)
차원 축소는 고차원 데이터를 더 낮은 차원의 공간으로 변환하여 데이터의 핵심 구조나 패턴을 유지하면서 불필요한 정보나 노이즈를 제거하는 과정이다.
주로 데이터의 시각화, 계산 효율성 향상, 과적합 방지 등을 목적으로 사용된다.
대표적인 기법 : PCA(주성분 분석), t-SNE, UMAP 등
차원 축소는 수백 개의 변수로 구성된 복잡한 데이터를 2차원이나 3차원으로 압축해도 주요 정보를 유지할 수 있도록 도와주며, 특히 데이터 간의 유사성이나 군집 구조를 직관적으로 파악하는 데 유용하다.
2. PCA
PCA(주성분 분석, Principal Component Analysis)는 고차원 데이터를 보다 낮은 차원으로 변환하면서도, 데이터의 분산(정보)을 최대한 보존하는 차원 축소 기법이다.
PCA는 원본 데이터에서 상관관계를 분석해 가장 큰 분산을 가지는 방향(주성분)을 찾고, 이 방향을 기준으로 데이터를 재투영하여 주요 특성만 남긴다.
이를 통해 노이즈를 줄이고 계산 효율을 높이며, 시각화나 전처리에 유용하게 활용된다.
PCA는 선형 변환 기법이며, 각 주성분은 서로 직교(orthogonal)한다.
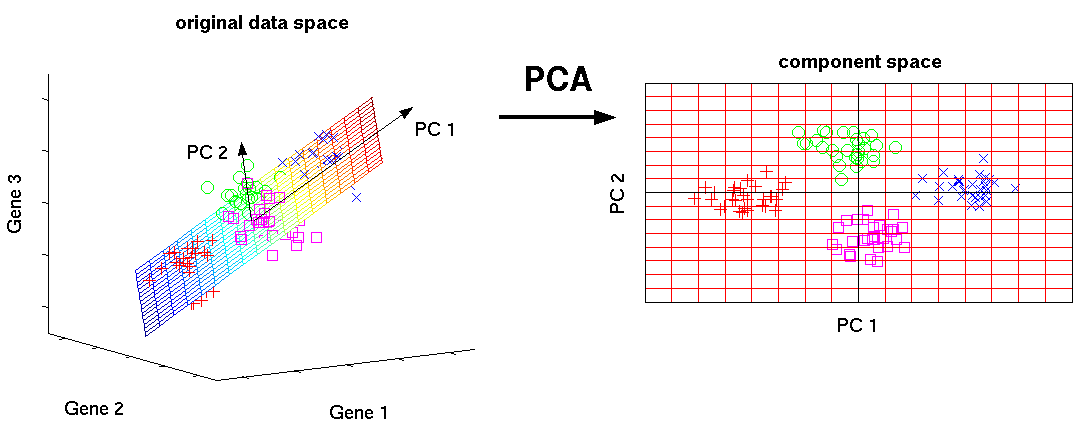
PCA의 단점
- 데이터 구조가 비선형(곡선 형태, 매니폴드 구조)이면 중요한 패턴을 잃어버릴 수 있음
- 변수마다 단위나 범위가 다르면, 분산이 큰 변수 쪽으로 주성분이 치우치게 됨(PCA 사용하려면 반드시 표준화가 필요함)
- PCA는 분산이 큰 방향을 중요하게 생각하기 때문에 노이즈가 크면 잘못된 축을 잡을 수 있음
3. 매니폴드 가정(Manifold Hypothesis)
매니폴드 가정(Manifold Assumption)은 고차원 데이터가 실제로는 훨씬 더 낮은 차원의 매끄러운 곡면(매니폴드) 위에 놓여 있다고 보는 가정이다.
데이터는 전체 고차원 공간을 가득 채우는 것이 아니라, 저차원 구조를 따라 분포한다는 의미이다.
이 가정은 차원 축소 기법(PCA, t-SNE, Isomap 등)이나 딥러닝에서의 표현 학습에서 핵심적인 이론적 기반이 되며, 복잡해 보이는 데이터도 저차원에서의 규칙성과 구조를 통해 더 잘 이해하고 처리할 수 있다는 통찰을 제공한다.
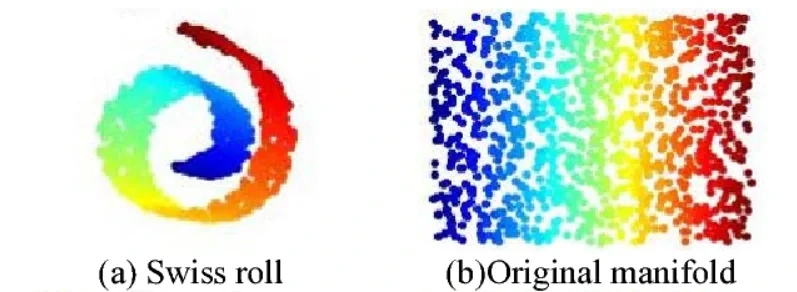
4. t-SNE
t-SNE(t-Distributed Stochastic Neighbor Embedding)는 고차원 데이터를 2차원이나 3차원으로 줄여 시각화하는 데 자주 쓰이는 차원 축소 기법이다.
매니폴드 가정(manifold assumption)에 기반하여, 고차원 데이터가 사실은 저차원 매니폴드 위에 놓여 있다고 보고 국소적인 구조(근접한 점들의 관계)를 잘 보존하도록 한다.
구체적으로는 고차원 공간에서 이웃한 점들이 가질 확률 분포와 저차원 공간에서의 확률 분포가 비슷해지도록 최적화하며, 특히 t-분포를 사용해 군집 사이의 거리를 더 넓게 벌려주는 효과를 낸다.
→ t-SNE는 복잡한 데이터의 잠재적인 패턴을 시각적으로 잘 드러낼 수 있다.
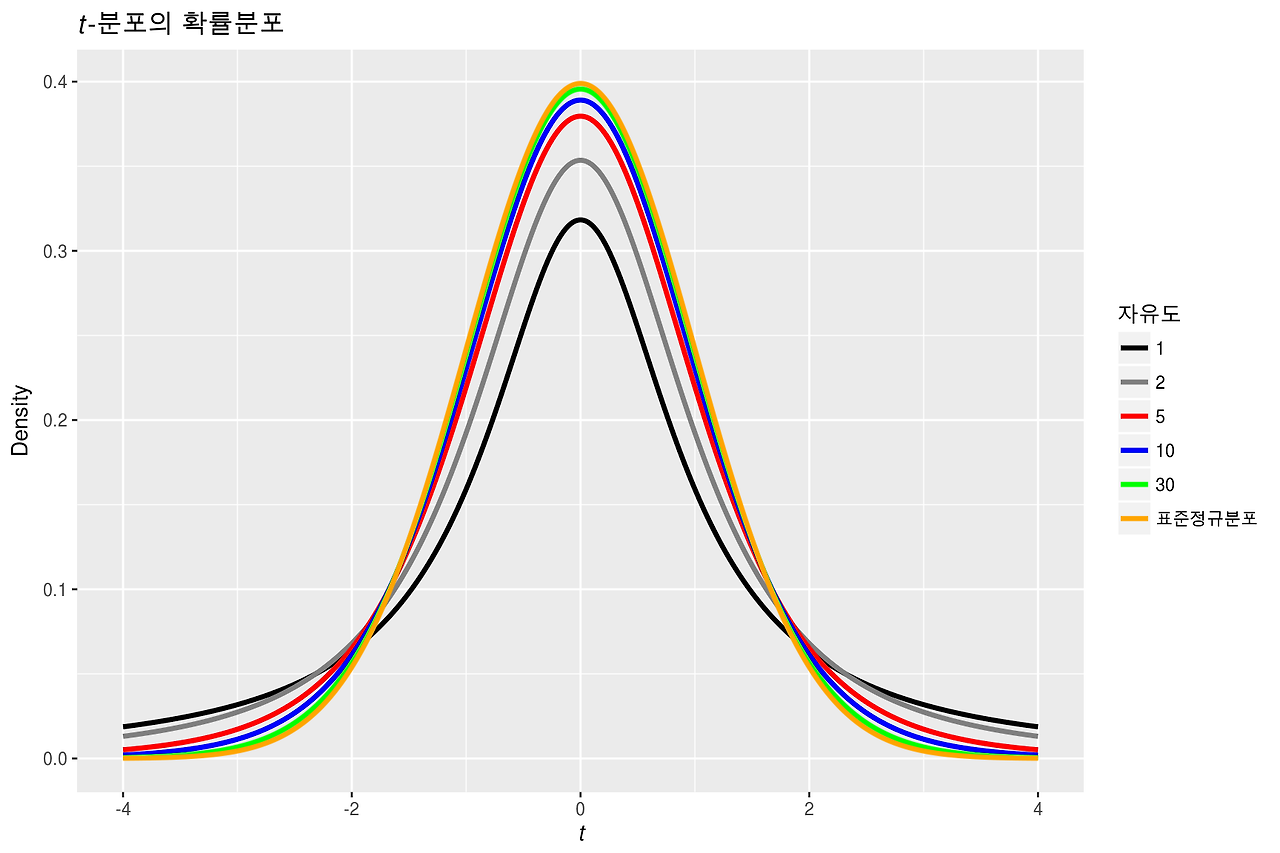
t-분포를 사용하는 이유
- 정규분포(가우시안): 가운데 뾰족하고, 멀리 가면 값이 너무 빨리 작아짐
→ 멀리 떨어진 점들을 잘 구별 못함 - t-분포: 가운데는 정규랑 비슷하지만, 꼬리가 두꺼움
→ 멀리 떨어진 점도 “완전히 0” 취급하지 않고, 적당히 떨어져 있다고 표현 가능
5. UMAP
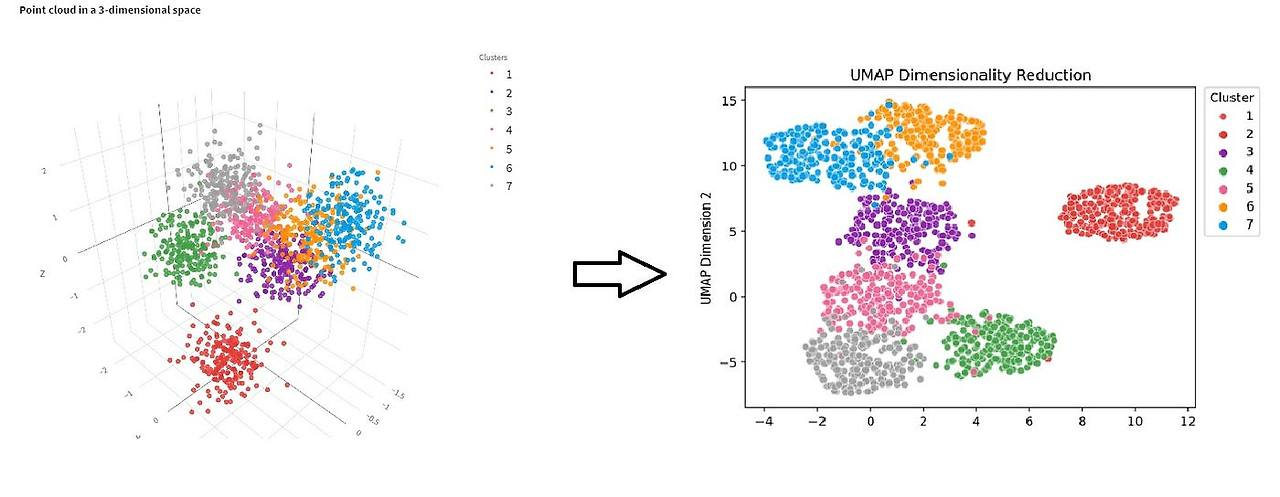
UMAP(Uniform Manifold Approximation and Projection)은 고차원 데이터를 저차원 공간으로 효율적으로 축소하는 비선형 차원 축소 기법이다.
t-SNE보다 속도가 빠르고 전체 구조와 국소 구조를 모두 잘 보존하는 것이 특징이다.
UMAP은 매니폴드 가정과 위상 공간 이론을 바탕으로, 고차원 공간에서의 이웃 관계를 저차원에서도 유지하려고 하며, 군집의 형태나 거리, 밀도 정보까지 어느 정도 보존한다.
클러스터링 전처리, 특징 추출, 노이즈 제거 등 다양한 머신러닝 작업에 활용된다.
최근 연구에서는 t-SNE와 UMAP의 초기값 설정(initialization)이 시각화 품질과 신뢰도에 큰 영향을 미친다는 의견이 많아지고 있다고 함.
특히 t-SNE에서는 초기값을 PCA로 설정할 경우, 랜덤 초기화보다 더 안정적인 구조 보존과 재현성이 높아지는 것으로 보고되고 있으며,
UMAP에서도 PCA 기반 초기화가 더 나은 전역 구조를 유지한다는 결과가 나타나고 있다고 함.
→ 차원 축소 결과에 대한 해석의 신뢰성을 높이기 위한 중요한 고려 요소.
단순히 알고리즘만 선택하는 것이 아니라 초기화 방법까지 설계에 포함해야 한다는 인식이 확산되고 있다.

import numpy as np
from umap import UMAP
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from torchvision.datasets import MNIST, CIFAR10# MNIST와 CIFAR10 데이터셋 다운로드 (PyTorch Dataset 형식)
mnist = MNIST(root='.', train=True, download=True)
cifar10 = CIFAR10(root='.', train=True, download=True)# PyTorch Dataset → scikit-learn에서 다루기 쉽게 numpy 배열로 변환하는 함수
def convert_sklearn_dataset(pytorch_dataset):
X, y = [], []
for image, label in pytorch_dataset:
x = np.array(image) # PIL 이미지를 numpy 배열로 변환
x = x / 255 # 픽셀 값을 [0,1] 범위로 정규화
X.append(x)
y.append(label)
X = np.array(X)
X = X.reshape(len(X), -1) # (N, 가로*세로*채널) 형태로 평탄화
y = np.array(y)
return X, y# 변환된 MNIST, CIFAR10 데이터셋 (numpy 기반)
mnist_X, mnist_y = convert_sklearn_dataset(mnist)
cifar10_X, cifar10_y = convert_sklearn_dataset(cifar10)# 퍼플렉서티 = 유효 이웃 수. 작게 잡으면 국소 구조 강조, 크게 잡으면 전역 구조 반영이며,
# 데이터 수와 구조에 맞춰 5–50(혹은 100) 사이에서 몇 개 값을 시험해 가장 안정적이고 해석 가능한 시각화를 고르는 것이 가장 안전
tsne_random = TSNE(n_components=2, perplexity=200, init="random", random_state=2025)
tsne_pca = TSNE(n_components=2, perplexity=200, init="pca", random_state=2025)np.random.seed(2025)
# 데이터가 너무 많으니 1000개만 샘플링
mnist_idx = np.random.choice(len(mnist_X), 1000, replace=False)
cifar10_idx = np.random.choice(len(cifar10_X), 1000, replace=False)# 임베딩 후 시각화 함수
def plot_embedding(model, X, y, idx):
X_set = X[idx] # 샘플링한 데이터
y_set = y[idx] # 해당 라벨
# 차원 축소 (예: t-SNE, UMAP)
X_set = model.fit_transform(X_set)
class_names = set(y_set) # 고유 클래스 집합
# 클래스별로 색을 달리해서 2D 공간에 산점도 표시
for i, class_name in enumerate(class_names):
plt.scatter(
X_set[y_set == class_name, 0],
X_set[y_set == class_name, 1],
color=plt.cm.tab10(i), # 10가지 색상 팔레트 사용
label=class_name,
)
plt.xlabel('component 0')
plt.ylabel('component 1')
plt.legend()
plt.show()# t-SNE(random init) 결과 시각화 (MNIST 데이터 1000개)
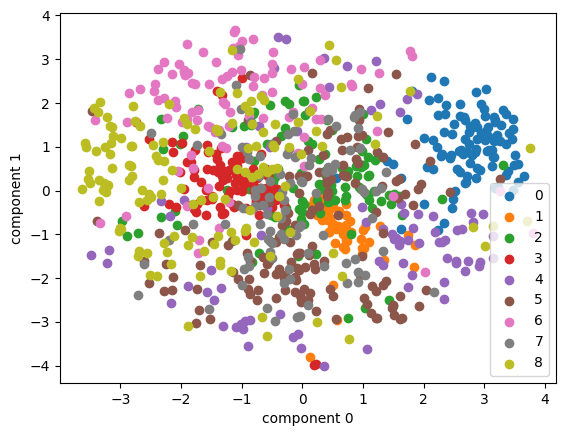
plot_embedding(tsne_random, mnist_X, mnist_y, mnist_idx)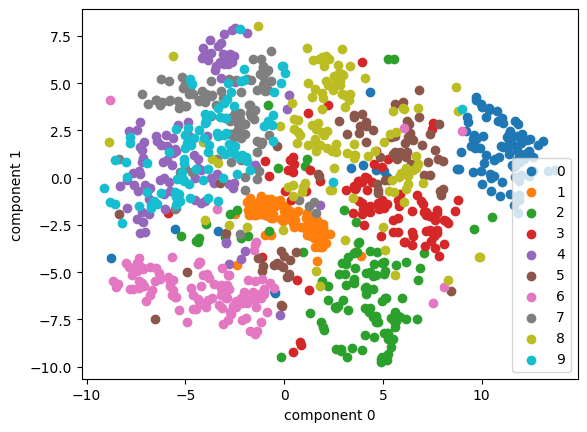
plot_embedding(tsne_pca, mnist_X, mnist_y, mnist_idx)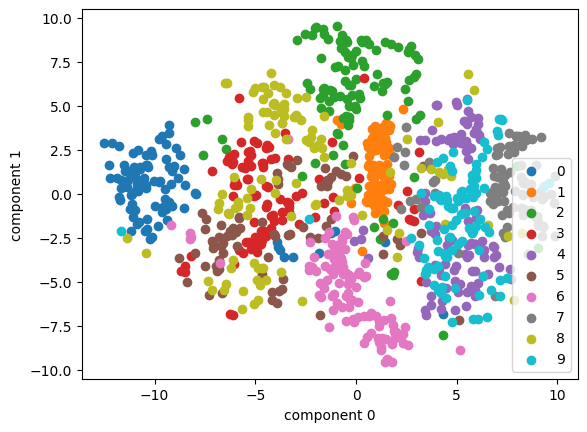
🔹 init="random"
- 임베딩 공간(2D)에서 무작위 좌표로 시작한다.
- 같은 데이터라도 random_state가 다르면 결과 시각화가 달라질 수 있다.
- 국소적인 구조(비슷한 점들이 모이는 패턴)는 안정적이지만, 전체적인 위치나 회전/뒤집힘은 랜덤에 따라 달라질 수 있다.
(색깔별 군집은 비슷하지만 그림 배치가 달라짐)
🔹 init="pca"
- 먼저 고차원 데이터를 PCA로 2차원에 줄인 후, 그 결과를 t-SNE의 초기 좌표로 사용한다.
- 랜덤 시작보다 안정적이고,
반복 실행 시 전체적인 레이아웃(위치, 방향)이 더 일관되게 나온다. - 특히 큰 데이터셋에서는 수렴 속도도 빠르고 안정적이다.
🤔 위의 그래프에서는 초기값이 랜덤이든 pca든 비슷해보여서 어떤 차이가 있는건지는 잘 모르겠다!
plot_embedding(tsne_random, cifar10_X, cifar10_y, cifar10_idx)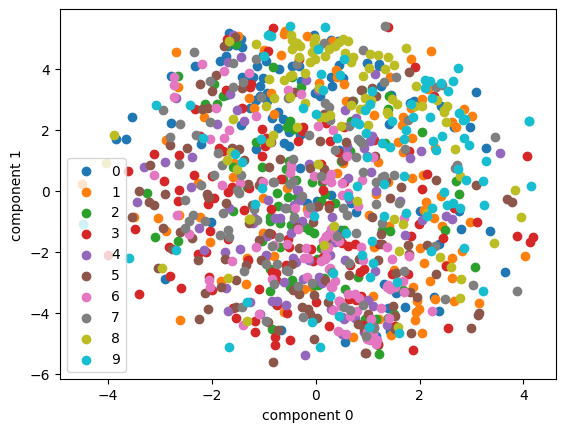
plot_embedding(tsne_pca, cifar10_X, cifar10_y, cifar10_idx)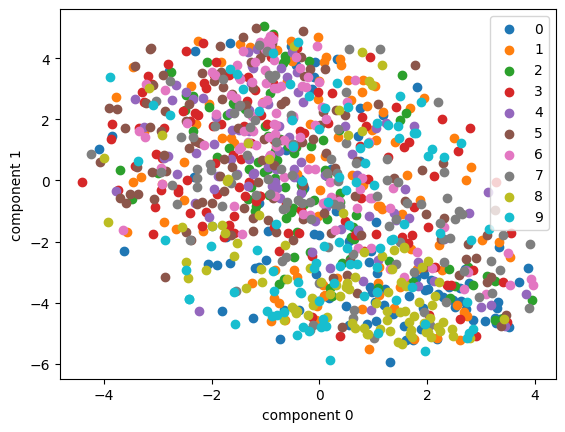
🤔 클래스별로 딱딱 모여 있지 않고, 섞여버렸다. 왜 그럴까?
CIFAR-10은 고차원 데이터
원래 CIFAR-10 이미지는 32×32 크기의 RGB → 3072차원 (32×32×3) 벡터이다.
이걸 2차원으로 압축하면, 원래의 복잡한 분포 정보 대부분이 손실된다.
→ 중요한 구조(클래스별 차이)가 사라지고, 단순히 "비슷한 픽셀 패턴" 정도만 남는다.
Raw Pixel 기반 표현의 한계
지금 차원 축소한 건 그냥 원본 픽셀 값이다.
하지만 CIFAR-10의 클래스(개, 고양이, 자동차 등)는 픽셀 단위가 아니라 추상적 특징(모양, 질감, 경계선)으로 구분된다.
→ 단순한 픽셀 값 공간에서는 클래스 간 차이가 잘 드러나지 않고, 서로 뒤섞여 버린다.
MNIST와의 차이
MNIST 같은 흑백 숫자 데이터는 픽셀 패턴만 봐도 "숫자 0"과 "숫자 1"이 쉽게 구분된다.
그래서 t-SNE나 PCA로 줄여도 클래스별로 잘 모여 보인다.
반면 CIFAR-10은 자연 이미지라 배경, 색깔, 포즈 다양성이 크기 때문에
단순히 픽셀 값만으로는 고양이와 개, 자동차와 트럭이 겹쳐서 구분되지 않는다.
차원 축소 알고리즘의 특성
PCA → 선형 변환이라 복잡한 비선형 경계는 못 잡음.
t-SNE → 지역적 구조는 잡지만, 데이터가 본질적으로 섞여 있으면 분리가 안 됨.
!pip install umap-learn# min_dist : 저차원 공간에서 점들이 얼마나 뭉칠 수 있는지를 조절
# n_neighbors : 가까운 이웃으로 간주하는 점의 개수, 값이 작으면 국소 구조 위주로 표현, 값이 크면 전역 구조까지 고려
umap = UMAP(n_components=2, min_dist=.05, n_neighbors=8, random_state=2025)
plot_embedding(umap, mnist_X, mnist_y, mnist_idx)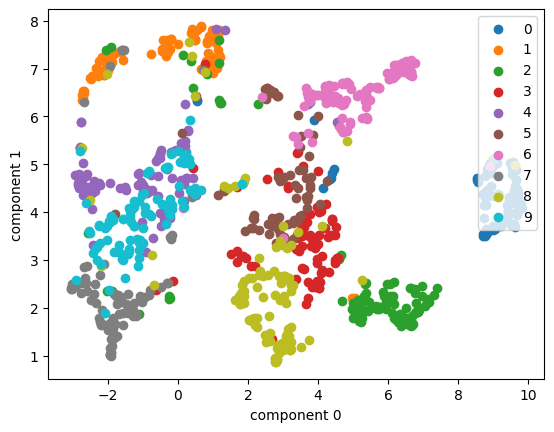
🤔 mnist 데이터셋에 umap으로 하니 클래스들 별로 잘 모여있는 모습이다.
plot_embedding(umap, cifar10_X, cifar10_y, cifar10_idx)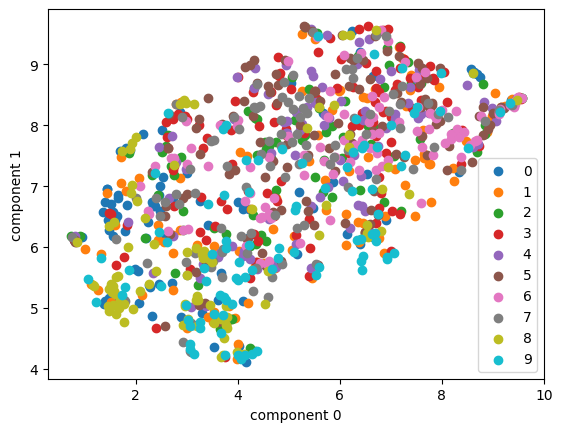
🤔 cifar10 데이터셋은 umap으로 해도 섞여있는 모습이었다.
import torch.nn as nn # PyTorch 신경망 모듈
# torchvision에서 제공하는 ResNet18 모델 (ImageNet으로 학습된 가중치 포함)
from torchvision.models import resnet18, ResNet18_Weights# 사전학습된 ResNet18 모델 불러오기 (ImageNet으로 학습된 가중치 사용)
feature_extractor = resnet18(weights=ResNet18_Weights.DEFAULT)
feature_extractor.fc = nn.Identity() # 분류하지 않고, 특징만 추출import torch
from torchvision.transforms import v2 # 새로운 transforms API (더 직관적)# 이미지 전처리 파이프라인 정의
transforms = v2.Compose([
v2.ToImage(), # NumPy/PIL → Torch Tensor 변환
# antialias=True, 크기를 줄일 때, 키울 때 생기는 깨짐(계단 현상)을 줄여서 부드럽게 리사이즈
v2.Resize(size=(96, 96), antialias=True),
# 원래 CIFAR10은 32x32, ResNet18은 더 큰 입력을 기대함 → 96x96으로 키움
v2.ToDtype(torch.float32, scale=True),
# 이미지 픽셀을 [0~255] → [0~1] 범위 float32로 변환
v2.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
# ImageNet 학습 시 사용된 평균/표준편차로 정규화
# 이렇게 맞춰줘야 ResNet18의 사전학습 성능을 제대로 활용할 수 있음
])cifar10_imagenet = CIFAR10(root='.', train=True, download=True, transform=transforms)cifar10_imagenet_X = torch.stack([cifar10_imagenet[idx][0] for idx in cifar10_idx]) # → 선택한 이미지들을 전처리해서 Tensor로 묶음
cifar10_imagenet_y = np.array([cifar10_imagenet[idx][1] for idx in cifar10_idx]) # → 선택한 이미지들의 라벨만 따로 NumPy 배열로 저장
# ResNet18을 통해 특징 추출
# (분류 대신, 512차원 feature vector를 얻음)
feature_X = feature_extractor(cifar10_imagenet_X).detach().numpy()plot_embedding(tsne_pca, feature_X, cifar10_imagenet_y, list(range(len(cifar10_imagenet_y))))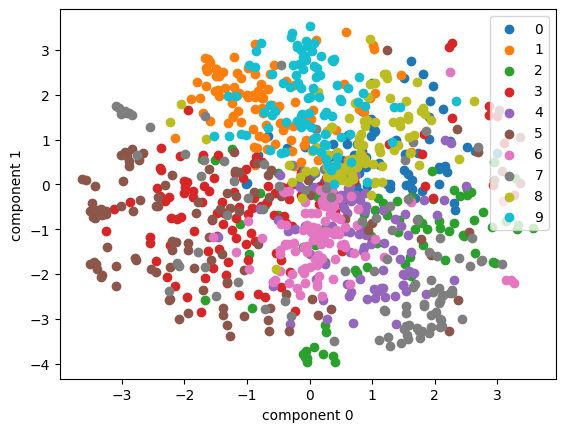
# MedMNIST 라이브러리 설치 (의학 데이터셋 모음집)
!pip install medmnistimport medmnist
print(f"MedMNIST v{medmnist.__version__}")MedMNIST v3.0.2from medmnist import INFO
# 1. pathmnist(위장 내시경 이미지 데이터셋) 정보 불러오기
pathmnist_info = INFO['pathmnist'] # 딕셔너리 형태의 정보
DataClass = getattr(medmnist, pathmnist_info['python_class'])
# pathmnist에 해당하는 Python 클래스 동적으로 가져오기# 2. 데이터 다운로드 및 로드
pathmnist = DataClass(split='train', download=True)
# train split만 가져오기
pathmnist.montage(length=20)
# 데이터 샘플 20개짜리 이미지 타일로 출력 (시각화용)
# 3. sklearn에서 쓰기 편하게 변환
pathmnist_X, pathmnist_y = convert_sklearn_dataset(pathmnist)
pathmnist_y = pathmnist_y[:, 0]
# label이 2차원으로 나와서 1차원으로 변환
pathmnist_y # 예: array([0, 4, 7, ..., 2, 0, 2]) 라벨값 출력array([0, 4, 7, ..., 2, 0, 2])# 4. 랜덤으로 1000개만 샘플링해서 사용
pathmnist_idx = np.random.choice(len(pathmnist_X), 1000, replace=False)
# 5. 특징 차원 축소해서 2D로 시각화 (랜덤 임베딩)
plot_embedding(tsne_random, pathmnist_X, pathmnist_y, pathmnist_idx)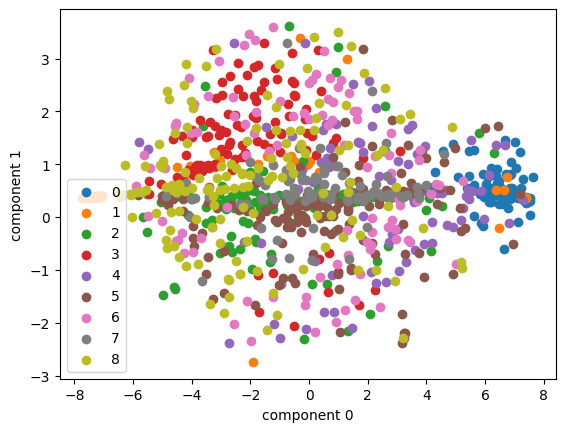
plot_embedding(tsne_pca, pathmnist_X, pathmnist_y, pathmnist_idx)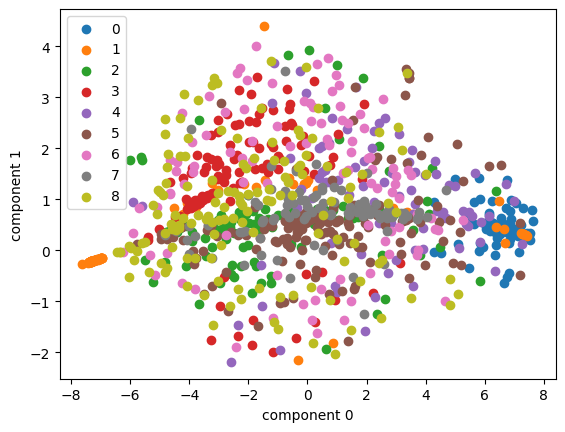
# 6. transform 적용해서 (리사이즈, 정규화 등) 학습된 모델에 맞게 변환
pathmnist_imagenet = DataClass(split='train', download=True, transform=transforms)
# 7. 인덱스(1000개) 데이터만 가져오기
pathmnist_imagenet_X = torch.stack([pathmnist_imagenet[idx][0] for idx in pathmnist_idx])
pathmnist_imagenet_y = np.array([pathmnist_imagenet[idx][1] for idx in pathmnist_idx])[:, 0]
# 8. ResNet18로 특징 추출 (fc=Identity로 바꿔서 분류 안 하고 feature만 가져옴)
feature_X = feature_extractor(pathmnist_imagenet_X).detach().numpy()# 9. PCA + t-SNE로 차원 축소해서 2D 좌표로 시각화
plot_embedding(tsne_pca, feature_X, pathmnist_imagenet_y, list(range(len(pathmnist_imagenet_y))))