빌드업
개인적으로 인공지능이 (AI) 란 단어 자체를 처음 접해본 것은 게임에서 였다. 어렸을때 유명했던 스타크래프트나 체스게임, 그리고 더 나아가 리그 오브 레전드에서도 AI, BOT 이란 이름으로 인공지능을 처음 접했던 것 같다. 그만큼 인공지능이라는 기술이 게임에서도 많이 접목이 되며 굉장히 적극적으로 사용이 되는 분야라고 생각한다. 자연스럽게 이번 과목의 다음 굵직한 챕터는 Game Playing (게임 인공지능) 에서 사용되는 인공지능 기술과 알고리즘을 다루는 내용이 들어있다.
Isolation Game
인공지능을 적용할 수 있는 게임은 굉장히 다양할 것 이라고 생각한다. 체스, 틱택토, 오목 같이 유명한 게임들이 있지만 이 과목에서는 Isolation Game (고립게임..?) 을 기반으로 강의를 진행한다. 고립게임의 룰은 간단하다. 체스판과 같은 사각형의 게임판에서 번갈아가며 자신의 말을 이동시킨다. 이동하는 방법은 체스에서 퀸과 동일한 방법으로 이동한다. 말이 이동한 뒤, 본인이 있었던 칸은 막힘처리가 된다. 본인과 상대방 말 모두 상대방 말과 막힌 칸으로 움직일 수 없으며, 상대방 말과 막힌 칸을 통과해서 이동 할 수 없다. 밑의 그림을 참고하자: 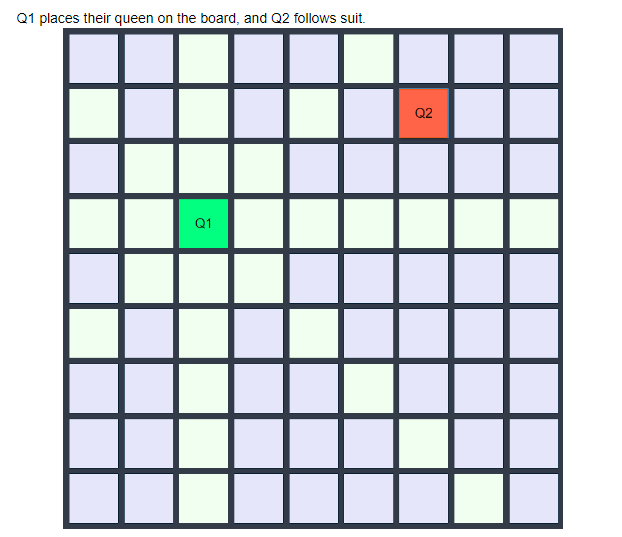
지금은 Q1, Q2가 있으며 초록색으로 된 칸은 이번 턴에 Q1이 움직일 수 있는 가능한 칸들이다. 지금은 각 플레이가 한번씩 턴을 사용한 것이며 (첫번째 턴에는 아무곳에나 자신의 말을 위치 시킬 수 있다) 이제 Q1의 두번째 턴임을 알 수 있다. Q1이 움직인 뒤에는 보드가 이런 식으로 바뀐다.
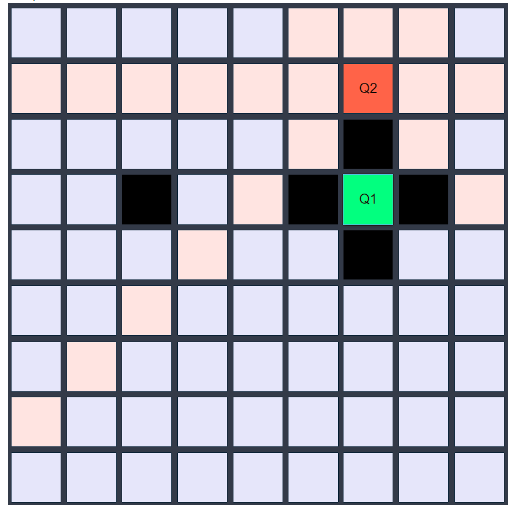
검정색 칸들이 막힌 칸 이라고 생각하면 되겠다. 위에 설명한 게임과 살짝 룰이 다른데, 이 예제에서는 말이 2칸 이상을 움직일 경우 움직이고 난 뒤 본인의 상하좌우도 막히는 추가 룰이 생겨서 저렇게 표기가 된 것이다. 아무튼 이 뒤에 있는 설명들에서는 이 추가룰은 없는 상태로 진행 할 것이니 참고하길 바란다. 보이는 것 처럼 Q2는 밑으로 이동할 수 없으며 막힌길을 관통하지 못하는 것을 알 수 있다 (빨간 칸들이 밑으로는 존재하지 않는다).
이렇게 플레이어가 번갈아가며 플레이를 하다보면 결국 어떤 플레이어가 움직이지 못하는 상황이 올 것이다. 그렇게 되었을 때, 마지막으로 자신의 턴을 사용한 플레이어가 이기는 게임이 isolation game이라고 생각하면 된다.
MiniMax Algorithm (최소최대 알고리즘)
이러한 게임을 무조건 이기게 하는 AI는 어떻게 작동해야할까? 간단하다. 최종게임까지의 "모든" 경우의 수를 계산하여 모든 결과를 미리 계산해 놓는다면 게임 상태가 어떠하든 그 상황에서 최적의 수를 둘 수 있을 것이다. 설명의 간소화를 위해, 강의에서는 오른쪽 밑에가 비활성화 된 2x3 사이즈의 판을 이용하며 이 글에서도 사용할 것 이다. 그러한 판의 모든 경우의 수를 계산하여 펼친다면 대략 이렇게 나온다: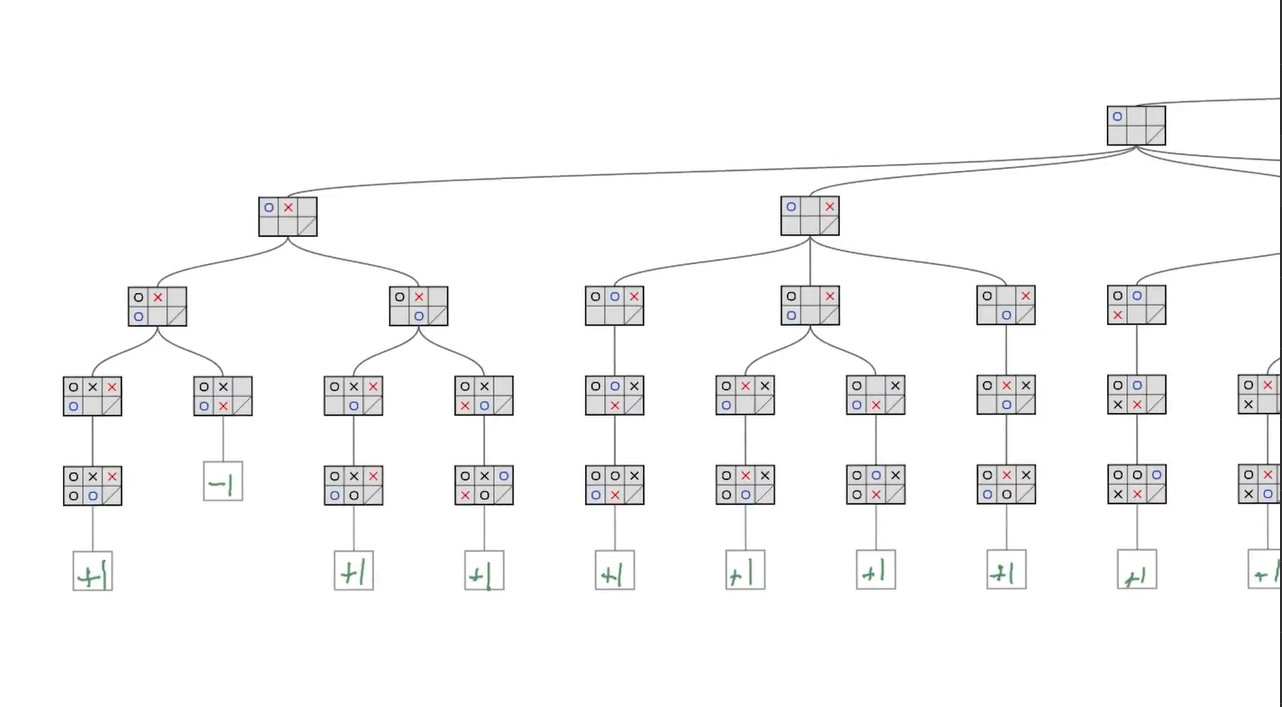
맨 밑에 적혀있는 +1 or -1은 우리의 AI 승패를 알려주며 +1은 승리를 -1은 패배를 의미한다. 고로 우리는 결국 +1을 향하는 알고리즘을 짜야하는 것이다. 상대방 또한 항상 주어진 상황에서 최적의 수만을 둔다는 가정을 할때 상대는 -1을 향해 본인의 수를 둘 것이다. 이 +1 (max 값) 과 -1 (min 값)을 향해 번갈아가며 돌아가는 게임같은 상황에서 minimax 알고리즘을 적용할 수 있다. 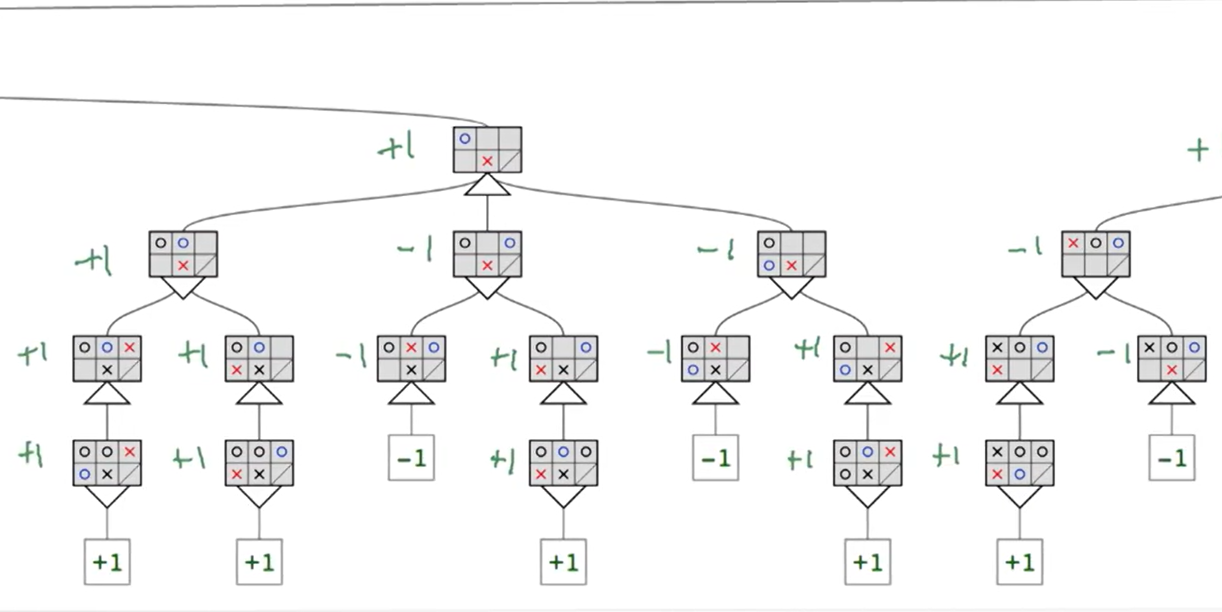
이제 게임판 밑에 위/아래로 향하는 화살표가 생겼다. 내 AI 턴에서 내 AI는 무조건 값을 Maximize 해야한다. 그것을 의미하는 것이 위로 향하는 화살표이며, 상대 AI턴에서 걔는 값을 최소화하기 때문에 화살표가 아래로 가 있는 것 이다. 강의에서는 맨 밑에서부터 이 숫자들을 설명하며 시작하는데 사실 시작부터 맨 밑을 보면 이 개념이 직관적이지가 않다. 그래서 지금 위에 그림 중 제일 위 branch를 보자. +1로 되어있으며 O,X 모두 한번씩 턴을 번갈아 놨으며, 지금 화살표가 위로 향해있기 때문에 O의 턴인것을 알 수 있다. 지금 상황에서 O가 놓을 수 있는 경우의 수가 3가지 있다. 한칸 오른쪽, 두칸 오른쪽, 밑. 각각 밑의 브랜치들도 +1 -1 값들을 가지고 있는데 이 -1 값의 경우의 수를 두면 결국 게임이 진다는 뜻을 의미한다 (실제로 한번 본인이 저기에 말을 옮기고 X가 최적의 수를 두면 결국 패배로 게임이 종료된다). 반대로 +1 쪽으로 움직이면 다음턴에 X가 어디로 가도 승리하게 된다.
이제 이 개념을 가진 상태로 제일 밑에서 부터 봐 보자. -1 +1 값들이 있는데 화살표가 아래로 되어있다면 있는 수 중에서 무조건 최소의 숫자만 선택을 한다. 보통 맨 마지막에서는 가지가 하나 밖에 없기때문에 밑에 숫자박스로 된 값을 고스란히 올려서 받게 된다. 이제 그 값들이 한칸 위로 전달이 되게 되는데 마찬가지로 화살표에 방향에 따라 가진 수 중에서 최소/최대 값중에 하나를 가져온다. 이제 밑에서 3번째 가지서부터 조금 선택지가 주어지게 되는데, 밑에서 3번째며 왼쪽에서 2번째인 가지를 봐 보자 (-1로 표기되어 있다 (O x O) 같이 생긴 칸이다). 이 턴에는 화살표가 밑으로 향하고 있으니, 상대턴이며 무조건 작은 값을 가져 갈 것이다. 그 브랜치에서는 상대는 두가지 선택지가 있다: 위 혹은 왼쪽. 하지만 왼쪽으로 가는 경우의 수는 +1 값을 가지고 있고 위로 가는 경우의 수는 -1 값을 가지고 있기때문에 상대방은 무조건 -1 값을 물려받으며 -1 값이 그 가지 (게임 state)값을 가지게 된다. 한칸 위로 가면 똑같은 논리로 위에 가지는 +1을 가지게 된다. 우리 AI는 본인이 이기는 +1 경우의 수로 게임을 진행 시킬테니 밑에 가지에서 가진 경우의 수 중 가장 큰 값인 +1값을 물려받게 된다. 이렇게 밑에서부터 쭉쭉 턴에 맞게 숫자를 가져오면 최대값을 가진 경우의 수로만 두게 되면 우리는 질 수가 없는 AI를 만들 수 있는 것 이다.
해치웠나?
참 쉽다. 참 쉬웠으면 좋겠다.
지금은 2x3사이즈의 게임판이지만 이게 5x5, 10x10으로 늘어나면 모든 경우의 수를 reasonable한 시간 내에 계산하는 것이 불가능 하다. 5x5 게임판만 하더라도 경우의 수가 25x24x23... 25! 값을 가지게 되는데, 요즘 최신 컴퓨터로 이 계산을 하더라도 몇억년이 걸린다. 그렇다면 이 계산을 어떻게 합리적으로 접근해야할 것 인가 는 다음 주차에 다루어 보도록 하겠다.
