실질적인 Game States
저번 주차에서 5x5 게임판의 모든 경우의 수를 계산하기 위해서는 25! 만큼의 계산량이 필요하다는 결과가 나왔었다. 하지만 이 결과값을 조금 더 현실적으로 볼 필요가 있다. 각 플레이어의 첫번째 턴에서는 사실 우리가 최적화 할 수 있는 방법이 별로 없다. 첫번째 플레이어가 25개의 선택지를 갖고, 두번째 플레이어가 첫번쨰 플레이어가 둔 수를 제외한 24개의 선택지를 가지는데엔 아무런 제약사항이 없기 때문이다. 그 이후부터는 어떻게 될까? 각 플레이어의 턴을 1-1, 2-1 같이 표현하도록 하겠다 (1번플레이어의 1턴, 2번플레이어의 1턴 등).
엄밀히 얘기하면 1-2, 2-2 부터 23, 22 가지의 경우의 수를 가지지 않는다. 그 이유는 플레이어들의 움직임에 제약사항이 있기 때문이다 (체스의 퀸 처럼 움직이며 막힌칸 or 상대말을 넘어 움직이기 불가능). 이런식으로 턴을 번갈아 가다보면 25! 의 값보다는 훨씬 적은 경우의 수가 존재한다는 것을 유추할 수 있다. 다만 이 값들이 정확히 얼마로 줄어들며, 각 턴마다 얼만큼씩 경우의 수들이 줄어드는 지도 모른다. 그래서 강의자는 여러 게임을 시뮬레이션을 돌려서 각 턴마다 (1-1 에서의 가능한 움직임 수,2-1,1-2,2-2... endgame * 여러게임) / net turn number 로 하여, 각 턴마다 평균적으로 몇 가지의 가능한 움직임 수를 구했다. 이렇게 평균적으로 가능한 움직임의 수 ^ 25 가 25! 보다 훨씬 더 under-estimate이며 조금 더 현실적인 값을 받을 수 있기 때문이다. 결론적으로 평균적으로 가능한 움직임의 수는 8 이었고, 8^25가 끝까지 계산하기 위한 연산 수 라는 것을 알게 되었다. 다만 이 값 마저도 몇 만년 단위가 걸리며 이 모든 경우의 수를 끝까지 계산하는 AI를 만들기는 지금 기술력으로는 불가능 하다는 것이 결론이었다.
그래서 뭐
그러면 여기서 그만 두어야 하는 것이냐? 그것은 아니다. 한정된 리소스에서의 최대한 검색을 한 뒤에 결정을 하는 방법 또한 존재한다. 사람이 한 수를 둔 뒤 2-5초내에 AI가 본인의 수를 두기를 기대하고, 그 길이가 10초가 넘어가면 좀 지루하다고 느끼기 시작한다는 연구결과가 있다. 그렇다면 우리가 경우의 수를 계산하는 기준을 end game까지 찾는 것이 아닌, 주어진 2-5초를 기준으로 찾을 수 있을 때 까지 찾아보는 방법도 있다. 그렇다면 2-5초까지 깊게 찾은 뒤에서는 어떤 어프로치를 가져가야 할까?
MiniMax 알고리즘에서 살짝 기준을 바꾸어 다른 측면에서 게임을 바라봐 보자. 게임을 이기려면 무조건 상대방 보다 놓을 수 있는 경우의 수가 더 많은 쪽으로 경기를 유도 해 나가야 한다. 그 뜻은 주어진 게임 상태에서 1번이 움직일 수 있는 타일 수 N과 2번이 움직일 수 있는 타일 수 M 개의 차이를 최대로 벌리면 게임을 유리하게 가져갈 수 있다는 뜻이다. 1번말의 움직임 갯수를 구하는 기능을 강의에선 Evaluation Function 이라고 부른다. 다시 5개 타일짜리 게임판으로 돌아가서 예시를 보겠다. 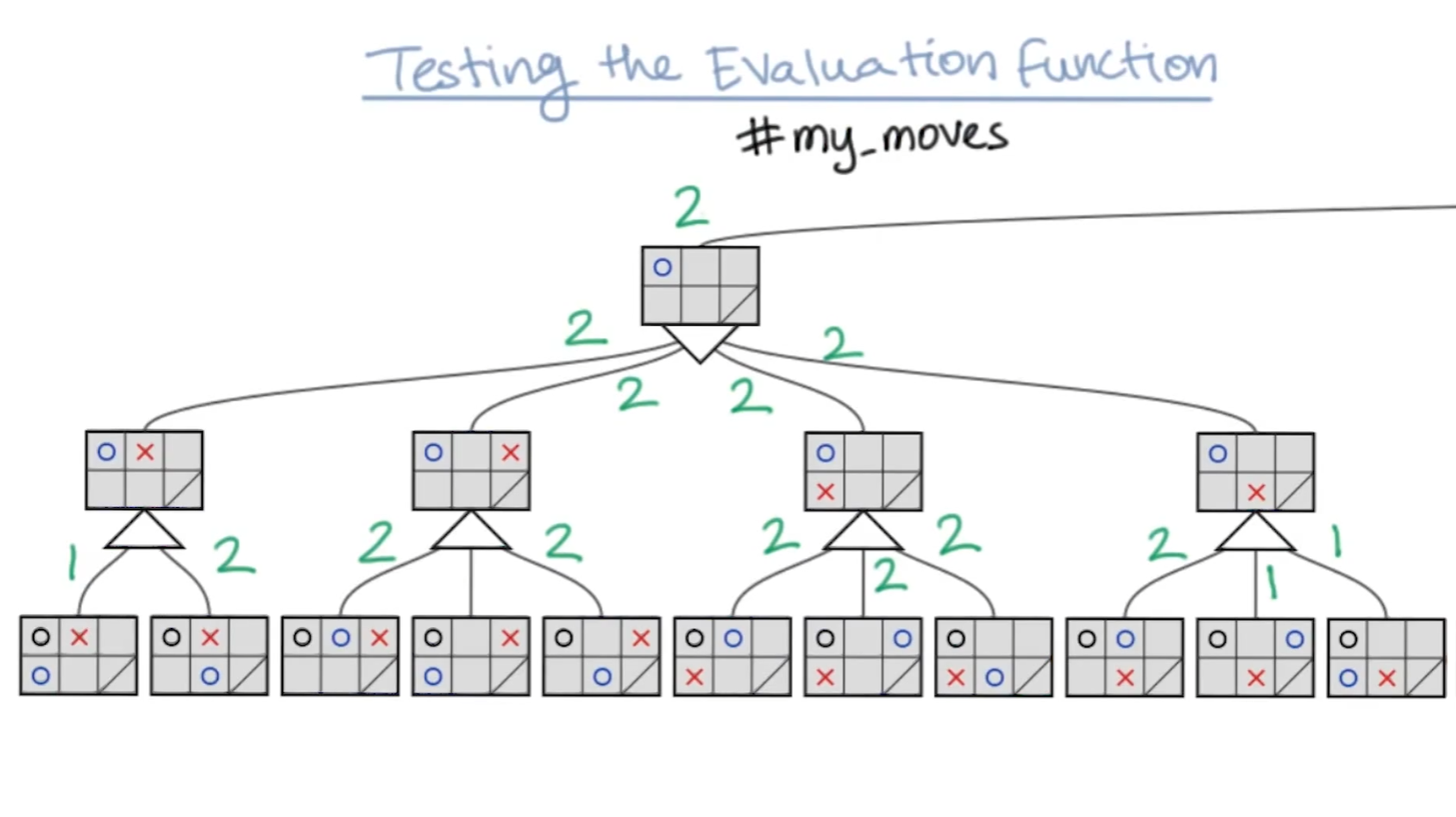
보이는 것 처럼 맨 밑에 각 상태마다 1번 플레이어가 움직일 수 있는 칸 수가 적혀있는 것을 알 수 있다. 1번 플레이어는 자신의 턴에 이 수를 minimax와 마찬가지로 maximize해야하기 때문에 저번 주차에서 설명했던 로직대로 더 큰 수를 위의 가지로 올리며 비슷한 형식으로 min max를 번갈아가면서 숫자가 올라가게 된다. 여기서 알아야 할 것은 가지의 끝까지 우리가 계산을 못 한다는 점이다. 그렇기에 1 깊이까지에서의 숫자를 가져와보고 2,3...6 깊이까지 찾아봤을때의 결과를 비교해 보았다.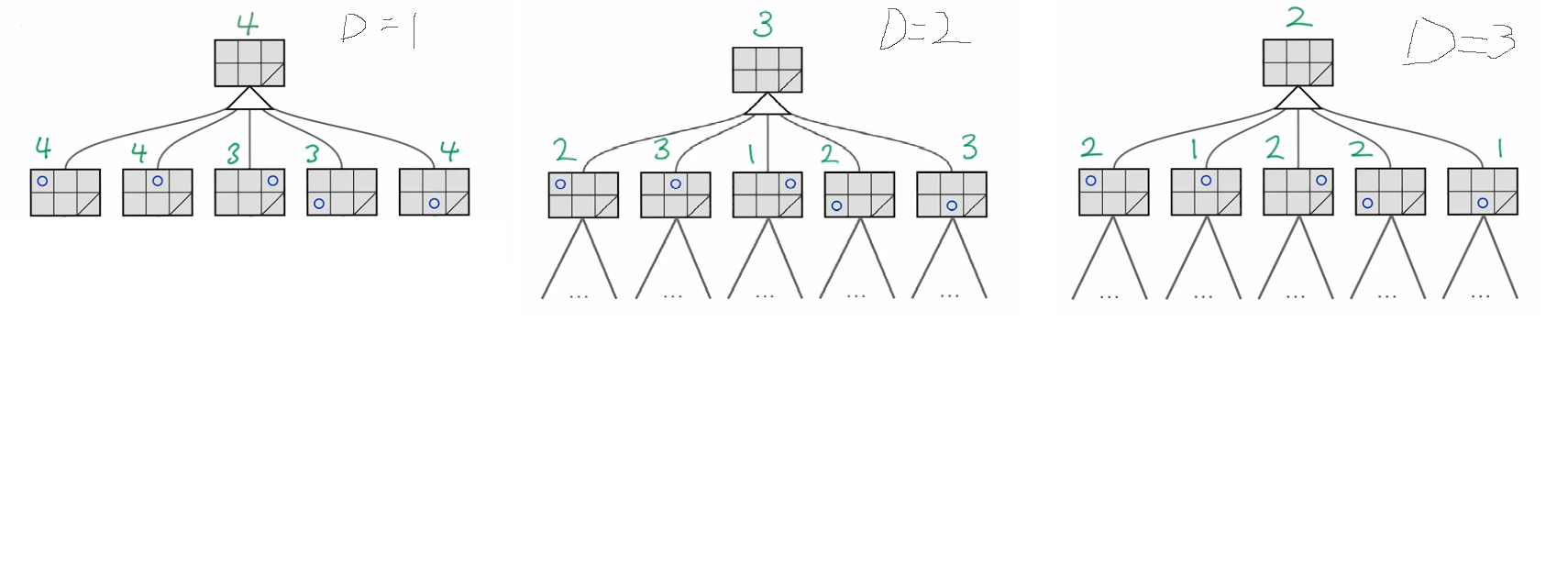
사진이 좀 넓어서 잘 안보일 수도 있지만, 제일 왼쪽이 깊이 1, 2, 3 순서로 evaluation function을 계산했을때의 결과이다. 보이는 것과 같이, 깊이 1일때는 1,2,5번째의 가지를 추천하지만 깊이 2에서는 2,5번째가지, 그리고 깊이 3에서는 1,3,4를 추천한다. 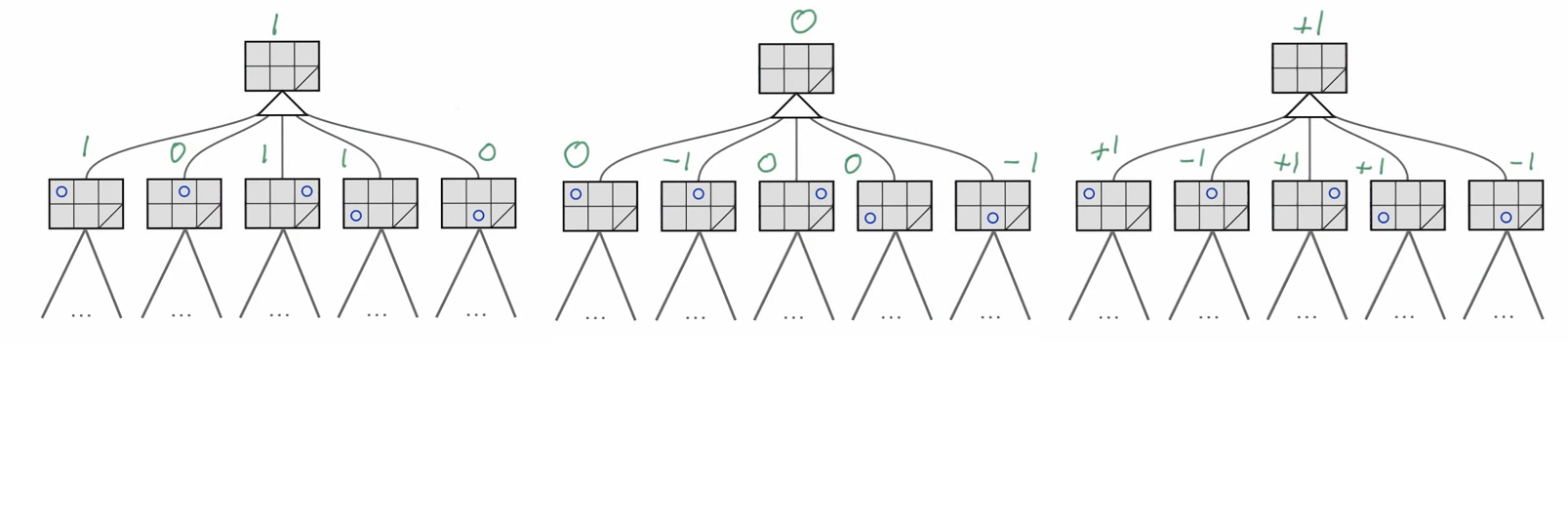
깊이 4,5,6에서도 추천하는 경로가 깊의 3과 완전히 동일한 것을 알 수 있다 (가지 1,3,4를 추천). 그래서 우리가 알아야 할 것은 추천하는 가지의 종류가 변하는 그 시점에서 조금 신중하게 골라야 할 필요가 있는 것이다. 이 알고리즘을 도와주는 것이 Iterative Deepening 인데 이 부분은 다음주에 더 깊이 다루어보도록 하겠다.
