Quiescent Search
저번 주차에서 얘기했던 것과 같이, 찾는 깊이 제한을 둘 때마다 결과 값 (승패 및 해당 game state 에서 가능한 경우의 수 값) 이 달라지는 경우도 있었고, 끝 깊이에 가까워 질 수록 결과가 converge 하는 것을 볼 수 있었다. 깊의 4 정도에서부터는 항상 동일한 결과 값 (동일한 패배 결과 값)을 반환 해 주는 것을 확인 할 수 있었다. 이 상태를 강의에서는 state of quiesence (직역하면 정지 상태?) 라고 표현했다. 왜냐하면 더 깊이 들어가도 값이 변하지 않는 정지 상태이기 때문인 것 같았다.
이 QS는 그러면 언제 유용할까? 보통 QS를 모든 게임상태에서 쓸 필요는 없다고 한다. 다만 게임 시작 상태 혹은 끝에 가까운 상태에서는 비슷한 결과물들을 내 주기 때문에 한정적인 자원 안에서 최적의 결론을 내기에 용이하다고 얘기한다. 이 QS의 개념과 더불어 Iterative Deepeing 이라는 알고리즘과 함께 결합하면 매우 좋은 성능의 게임 서치를 효율적으로 할 수 있다고 한다.
Iterative Deepening
결국 정지상태를 알기 위해선, 어찌되었든 굉장히 많은 깊이까지 서치를 해야하는 것은 변함이 없다. 저번 주차의 예시를 들면 결국 깊이 3,4 정도가 되었어야 QS를 찾지 않았는가? 그러면 결국 이게 무슨 의미가 있는 것 인가 - 에 대한 해답을 위해 ID 알고리즘이 나오게 된다. 물론 굉장히 깊은 단계까지 찾으면 더욱 승률이 높고 좋은 최적의 수를 둘 가능성이 높아진다. 다만 이전 주차들에서 다루었듯, 한정적인 계산량/계산시간을 고려를 하면서 최적의 답안을 내야하듯, 알고리즘 자체적으로 한정적인 깊이와 가지 수를 계산 할 수 밖에 없다.
전 주차에서 사용했던 예제를 한번 보자: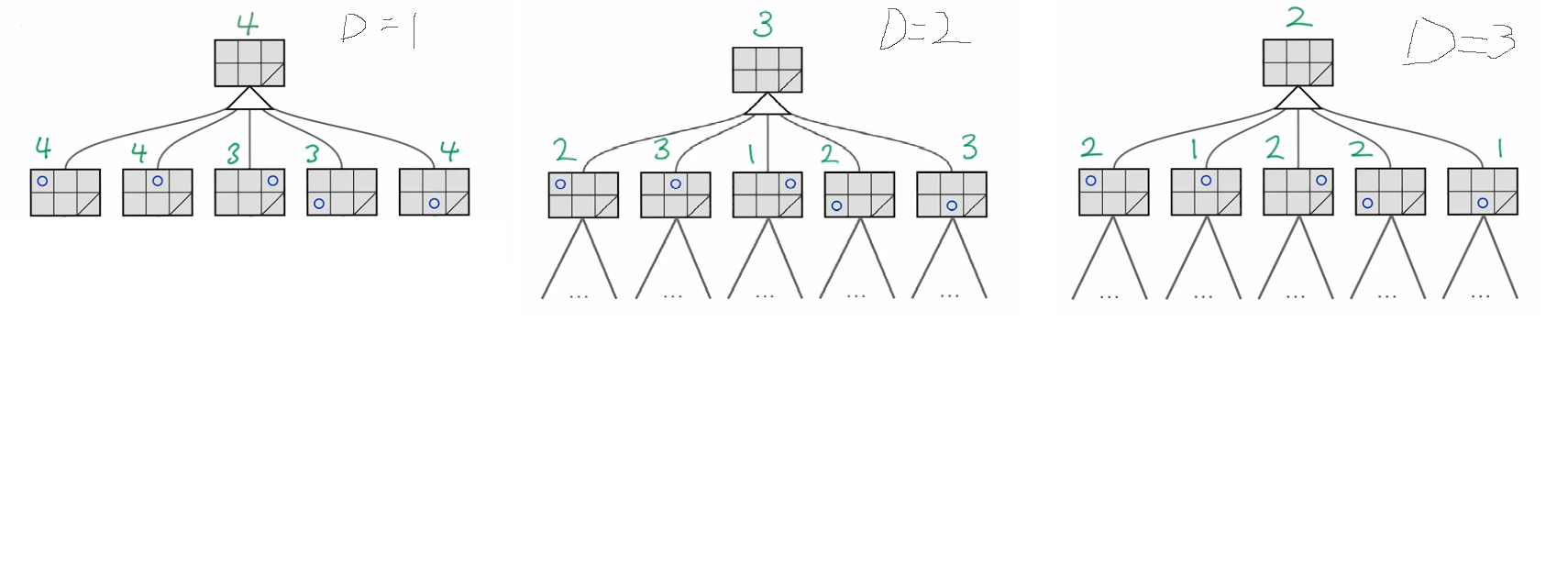
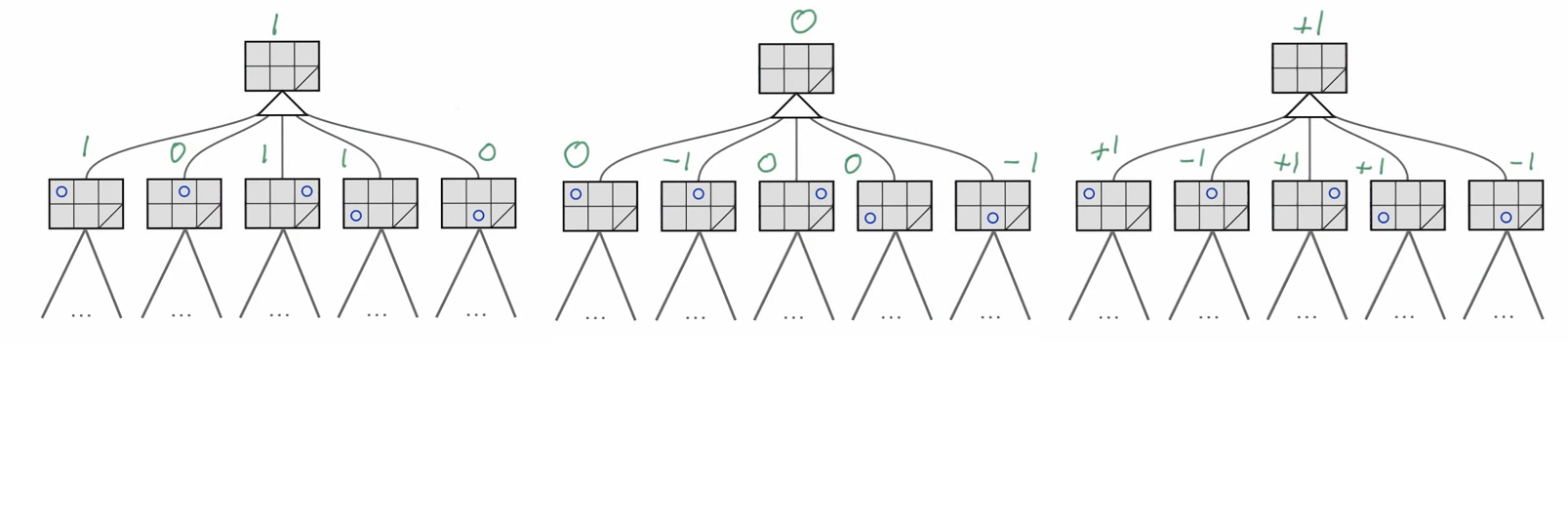
시간 및 계산량이 허용하는데 까지 계산을 한다고 했을때, D1까지에서는 1,2,5번째 (다 가지고 있어도 괜찮고 이 중에 하나만 가지고 있어도 괜찮음) 를 반환해주고 만약에 계산이 더 가능하다면 D2까지 거치하여 2,5번째 가지 값을 반환하고 그 후 D3, D4... 계산량과 시간이 가능한 수까지만 계산하여 거기서의 최적의 값을 반환 해 주는 알고리즘이 ID라고 한다.
그러면 여기서 질문이 있을 수 있다. 결국 이것 또한 계산량이 많아서 같은 것 아닌가? 답은 그렇지 않다. 2 개 가지 수를 가진 트리를 사용하여 계산해본다면 밑의 식 처럼 나오게 되는데: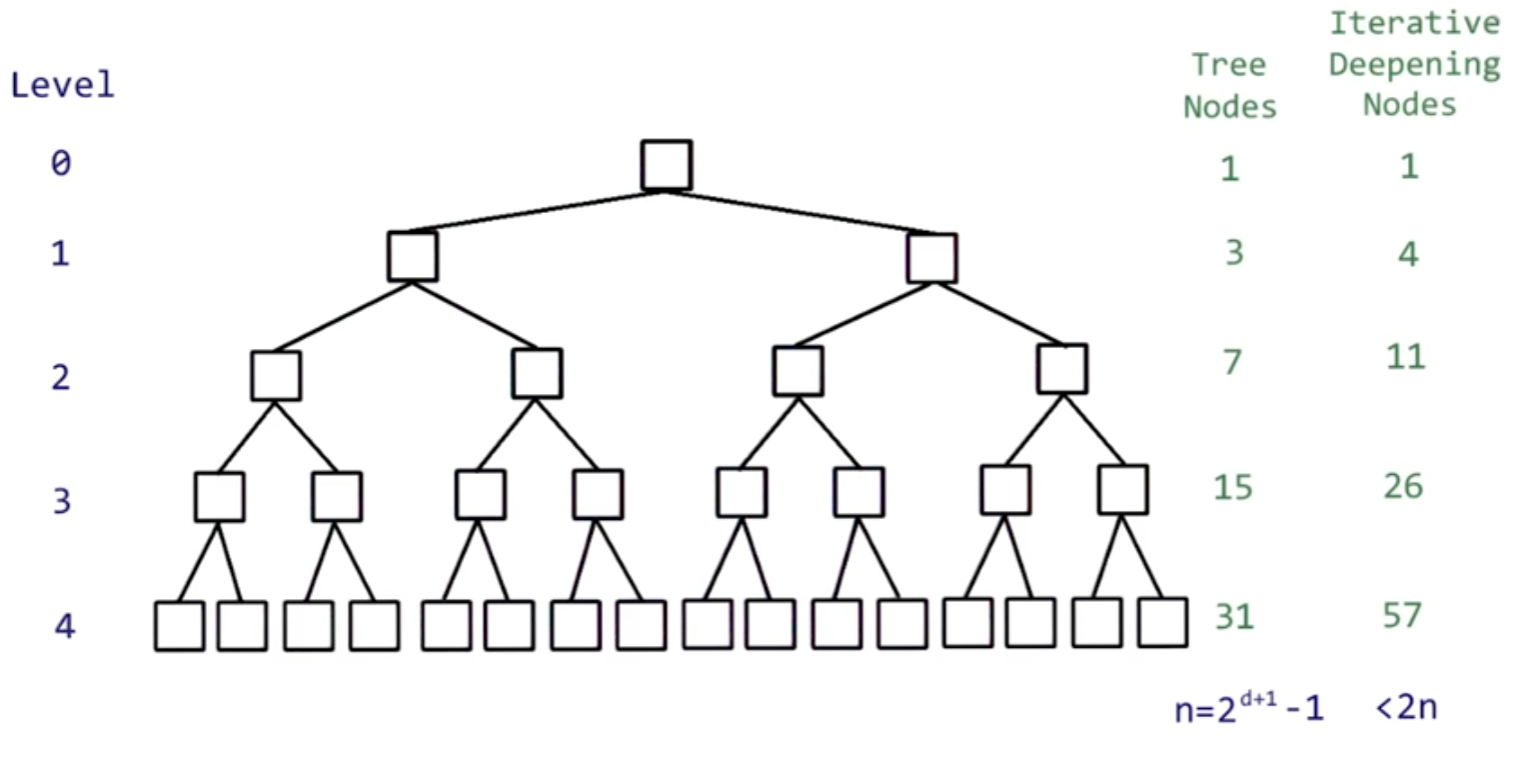
깊이가 깊어질 때마다 exponetial 로 증가되는 것이 아닌 multiplier 정도로 증가하기 때문에 비용이 그렇게 비싸지 않다는 것이다. 사실 더 놀라운 점은 이 계산량이 branch가 2가 아닌 3,4,5...n 개로 늘어나더라도 너무 과하게 계산량이 많아지지 않는 다는 것이다. 지금 위의 예에서는 branch 갯수가 2로 계산을 했지만 branching factor가 더 늘어나도 계산량은 크게 증가하지 않는다. 밑과 같은 계산식이 된다고 한다.
