Uniform Cost Search (UCS)
저번 주차에서 다루었던 BFS와 DFS 같은 경우에는 사실 굉장이 직관적이고 1차원적인 탐색 알고리즘이라고 생각한다. 물론 이거 직접 코딩해보려고 하니까 고려해야할게 꽤 많았다 사실 "옆으로 펼치는 것" vs "아래로 내려가는 것" 만 생각하면 되는 알고리즘들이기 때문에 이해하고 설명하는데에 큰 문제는 없다고 생각한다. 이번 주차에서 다루는 첫번째 알고리즘인 USC 또한 굉장히 직관적인 알고리즘이다.
저번 주차에서 다룬 BFS와 DFS는 "노드의 갯수/깊이"를 기준으로 잡아서 밑으로 갈 것인가 옆으로 펼칠 것인가 만 확인하고 진행시키면 됐었다. 이번에 설명할 UCS 같은 경우엔 Node가 기준이 되는 것이 아니라, 노드 A에서 노드 B로 가는데 소요되는 비용을 기준으로 frontier가 확장되게 된다. 예시로 저번주에 사용했던 그림을 사용하겠다.
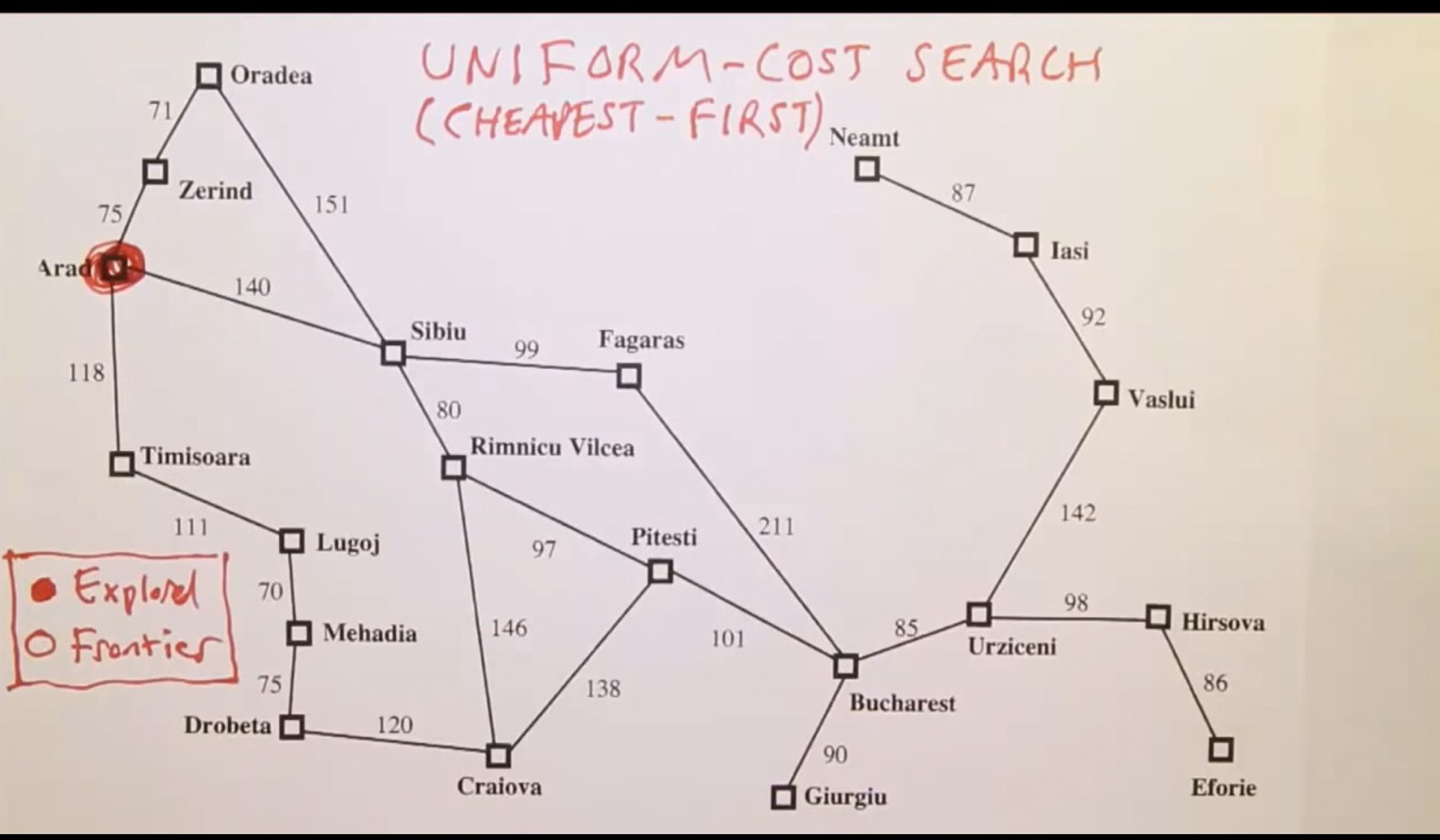
마찬가지로 Arad에서 시작하여 Bucharest로 도달한다고 가정해보자. Arad에서 붙어있는 이웃들인 Zerind, Sibiu, Timisoara가 있고, BFS나 DFS에서는 그냥 랜덤하게 하나를 골라 거기서부터 확장을 했었지만, UCS같은 경우 cost/weight를 기준으로 확장되기 때문에 가장 거리가 짧은 Zerind를 시작으로 탐색이 진행된다. 각 이웃들간의 cost들은 어떤 데이터 형태로 저장이 되어있고 그 노드간 cost값을 계속해서 비교하며 가장 짧은 cumulative cost값을 가진 노드로 확장하게 된다. 예시로, Zerind로 이동 탐색 한 후 Oradea, Sibiu, Timisoara가 다음 candidate node들이지만 Oradea 까지 이동하는데 75+71 코스트가 발생하고, Sibiu는 140, Timisoara까지는 118이 발생한다. 고로 다음 확장 노드는 Timisoara가 되겠다. 이런식으로 출발 노드를 기준으로 확장하는 cost값을 비교하여 가장 짧은 cost값을 가진 노드들을 순서로 확장하게 된다.
UCS 알고리즘 자체도 꽤나 직관적이다. cost값을 기준으로 확장하니, 노드값을 기준으로 한것과 비스무리한 흐름을 가진다. 여기서부터가 중요하다. UCS같이 cost값 혹은 거리값을 기준으로 확장을 하게 된다면, 당연히 가장 짧은 최적화된 거리를 찾을 수 있을 것이다. 이것을 좀 추상적으로 그림을 그려보면 이렇게 표현할 수 있다.

이런식으로 starting node에서부터 균일한 거리에 있는 모든 가능성들을 원 방향으로 서서히 확장시켜나가고, 결국 goal node에 도달하게 될 것 이다. 다만 이런식의 접근에는 큰 문제가 생긴다. 우리는 goal node와 starting node의 위치에 대한 정보가 있음에도 불구하고, 같은 cost에 있는 모든 노드들을 고려하기 때문에 굉장히 필요없는 많은 연산을 하게 된다는 것이다. 예를 들면, 위에 그림에서 위/아래/왼쪽 노드들에 대한 계산은 사실상 의미가 없다. 왜냐하면 우리가 찾고자하는 goal node의 위치는 starting node를 기준으로 오른쪽에 있기 때문이다. 우리는 starting/goal node의 위치 및 정보를 알고 있기때문에 그 정보를 기반으로 아래 그림처럼 탐색을 할 수 있을 것이다.

무조건 오른쪽으로 이동하면서, goal node에 가까워 지는 쪽으로만 탐색을 하게 하는 것이다. 이렇게 되면 필요없는 계산을 굉장히 줄일 수 있다는 장점이 있다. 여기서 문제가 있다는 것을 눈치 챘다면 당신은 아마 높은 확률로 탐색 알고리즘을 이미 알고 있는 사람일 것이다 왜 이 글을 읽고 있는 것인가. 탐색중에 obstacle, 즉 가로막고 있는 장애물이 존재하는 경우에는 이 알고리즘이 굉장히 부자연스러워진다. 아래 그림을 참고하자.
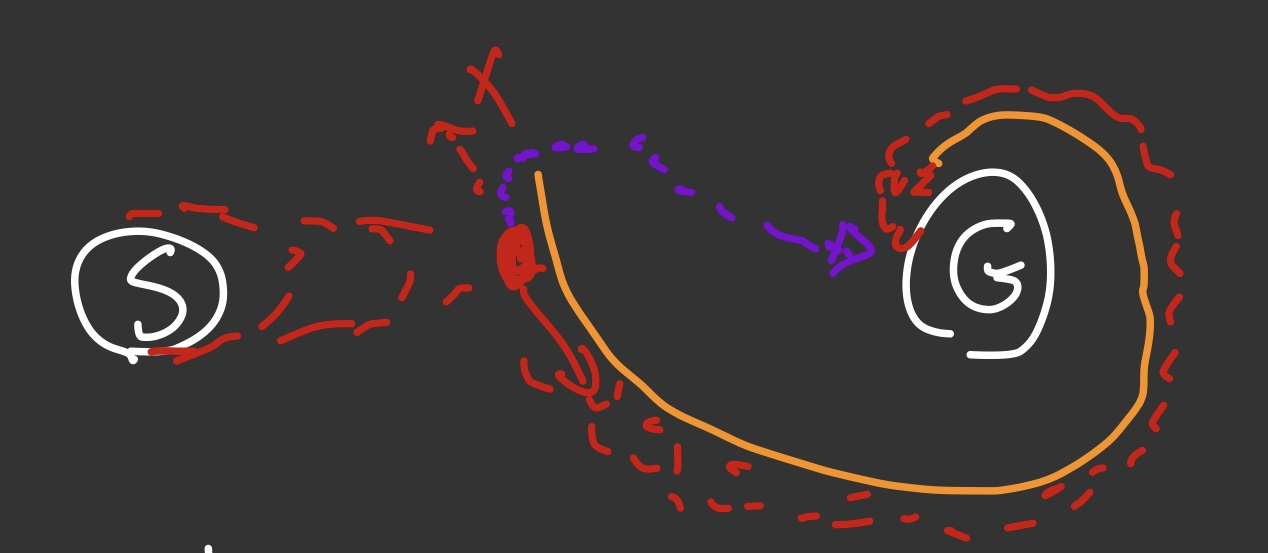
분명 탐색 알고리즘은 오른쪽으로 계속해서 goal node와 가까워지려고 펼쳐지고 있었다. 그러나 주황색의 장애물에 가로 막히는 일이 생겼다. 알고리즘에 의하면 탐색의 방향은 무조건 goal node와 가까워 지는 방향으로 펼쳐져야 하기 때문에 무조건 아래오른쪽 (5시방향)으로 탐색을 해야만 한다. 왜나하면 위로 돌아가는 짧은 길이 있음에도 불구하고, 위왼쪽 (11시방향)으로 가는 것은 goal node와 절대적인 거리를 늘리는 방향으로 탐색을 하는 것이기 때문에 해당 알고리즘에는 적합하지 않다. 보라색 길과 같이 훨씬 짧은 동선이 있음에도 불구하고, 알고리즘의 효율성을 위해 만들어놓은 로직이 오히려 더 비효율적인 동선을 나타내는 현상이 일어난다.
결국 계산의 효율과 (computational complexity) 최적화된 동선 (optimal path)를 두가지는 굉장히 다른 개념이다 만족하는 알고리즘이 필요한 것이다. 거기서 비롯된 알고리즘이 A* (A star 에이 스타 라고 부른다) 알고리즘이다.
생각보다 글이 길어져서 A star 알고리즘은 다음 주차에 적도록 하겠다.
