다층 퍼셉트론(multilayer perceptron: MLP)
입력층과 출력층 사이에 은닉층(hidden layer)을
가지고 있는 퍼셉트론
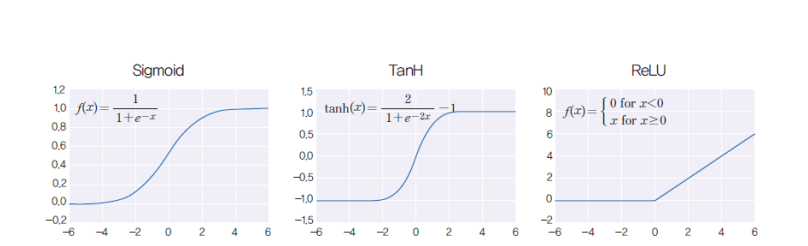
MLP에서는 다양한 활성화 함수를 사용한다.
일반적으로 많이 사용되는 활성화 함수
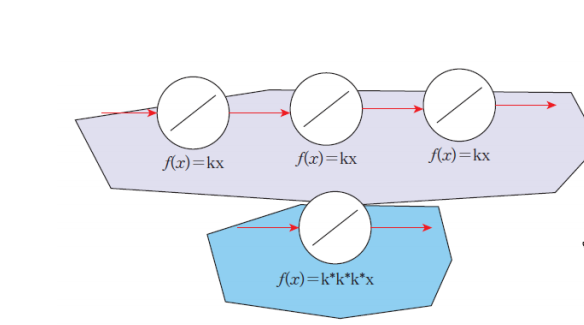
선형레이어는 많아도 쓸모가 없다.
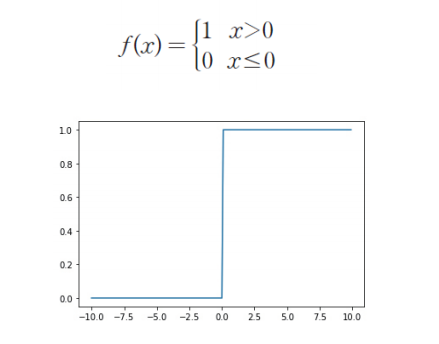
step function
계단 함수는 입력 신호의 총합이 0을 넘으면 1을 출력하고, 그렇지 않으면 0을 출력하는 함수이다.
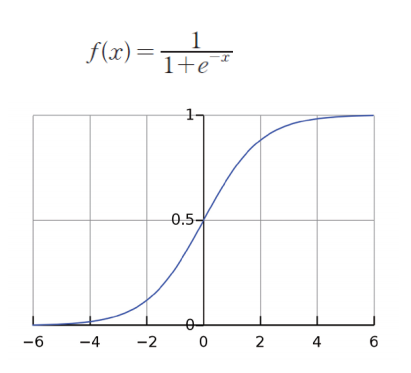
sigmoid function
S자와 같은 형태를 가지는 전통적인 활성화 함수
ReLU function(Rectifed Linear Unit function)
최근에 가장 인기 있는 활성화 함수이다.
입력이 0을 넘으면 그대로 출력하고, 입력이 0보다 적으면 출력은 0이 된다.
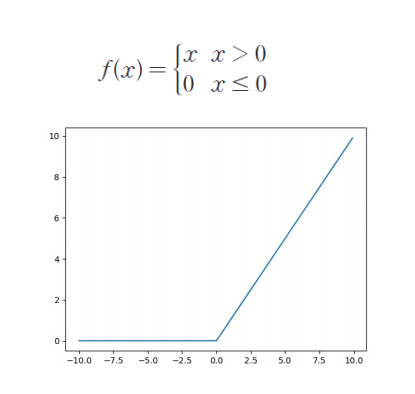
tanh function
시그모이드 함수와 아주 비슷하지만 출력값이 -1에서 1까지이다.
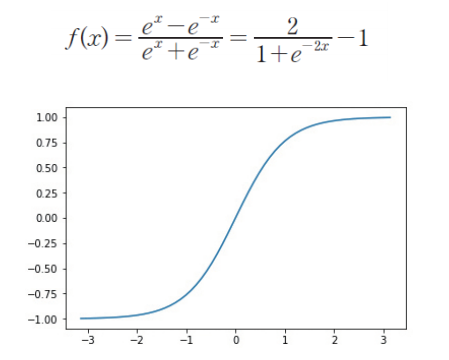
MLP의 순방향 패스
순방향 패스란 입력 신호가 입력층 유닛에 가해지고, 이 입력 신호가 은닉층을 통하여 출력층으로 전파되는 과정을 의미한다.
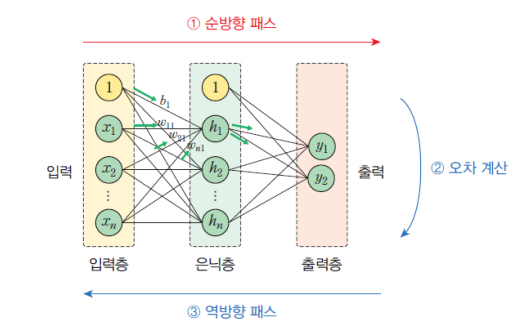
순방향 계산 예제

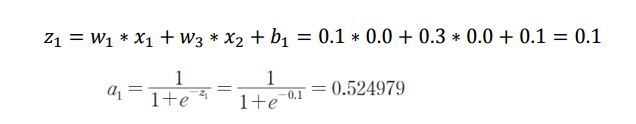
위는 h_1의 값을 계산하는 예제이다.
입력층 x_1,x_2 및 가중치와 편향을 이용해 z_1을 구하고 그 값을 활성화 함수에 대입해 최종적인 값을 구한다.
행렬로 구현하기
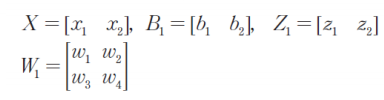
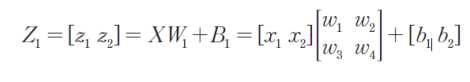
코드로 구현하기
import numpy as np
# 시그모이드 함수
def actf(x):
return 1/(1+np.exp(-x))
# 시그모이드 함수의 미분치
def actf_deriv(x):
return x*(1-x)
# 입력유닛의 개수, 은닉유닛의 개수, 출력유닛의 개수
inputs, hiddens, outputs = 2, 2, 1
learning_rate=0.2
# 훈련 샘플과 정답
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
T = np.array([[0], [1], [1], [0]])
W1 = np.array([[0.10, 0.20],
[0.30, 0.40]])
W2 = np.array([[0.50], [0.60]])
B1 = np.array([0.1, 0.2])
B2 = np.array([0.3])
# 순방향 전파 계산
def predict(x):
layer0 = x # 입력을 layer0에 대입한다.
Z1 = np.dot(layer0, W1)+B1 # 행렬의 곱을 계산한다.
layer1 = actf(Z1) # 활성화 함수를 적용한다.
Z2 = np.dot(layer1, W2)+B2 # 행렬의 곱을 계산한다.
layer2 = actf(Z2) # 활성화 함수를 적용한다.
return layer0, layer1, layer2
def test():
for x, y in zip(X, T):
x = np.reshape(x, (1, -1)) # x를 2차원 행렬로 만든다.
# 입력은 2차원이어야 한다.
layer0, layer1, layer2 = predict(x)
print(x, y, layer2)
test() 출력 결과
[[0 0]] [1] [[0.70938314]]
[[0 1]] [0] [[0.72844306]]
[[1 0]] [0] [[0.71791234]]
[[1 1]] [1] [[0.73598705]]MLP의 역전파 알고리즘
입력이 주어지면 순방향으로 계산하여 출력을 계산한 후에 실제 출력과 우리가 원하는 출력 간의 오차를 계산한다.
오차를 역방향으로 전파하면서 오차를 줄이는 방향으로 가중치를 변경한다.
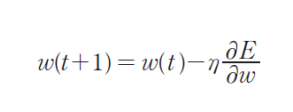
- 가중치와 편향을 0부터 1사이의 난수로 초기화한다.
- 수렴할 때까지 모든 가중치에 대하여 다음을 반복한다.
- 수렴함수 E의 그래디언트(미분값)을 계산한다.
- 학습률을 그래디언트에 곱해 기존 가중치 값에서 뺀다.
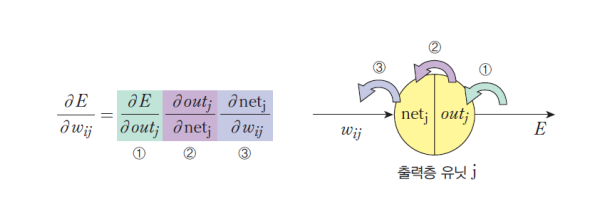
체인룰
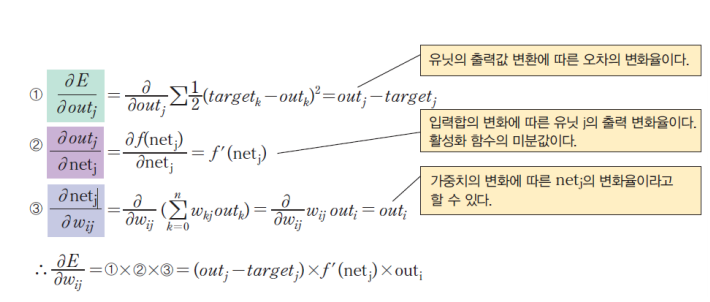
최종 계산
순방향
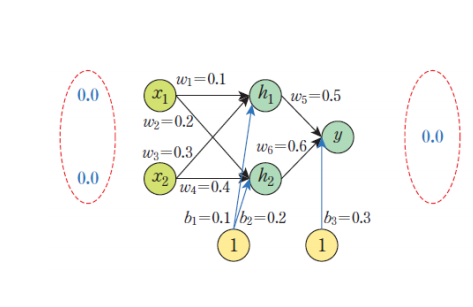
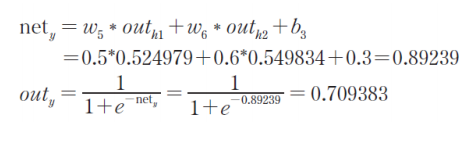
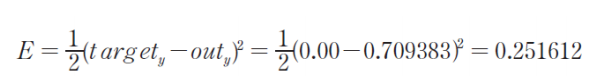
target = 목표값, out = 실제값
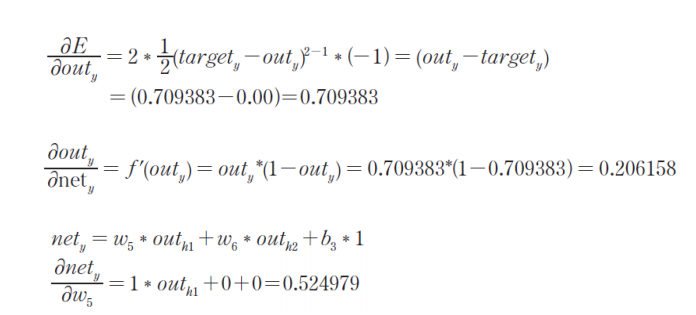
만약 바이어스를 구하는 문제라면, 마지막에 0 + 0 + b_3*1이 되는 것이다.
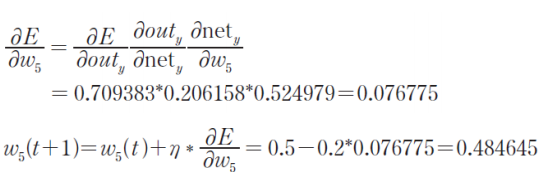
학습률은 0.2로 설정함.
