Perceptron

퍼셉트론(Perceptron)
1957년에 로젠블라트(Frank Rosenblatt)가 고안한 인공 신경망

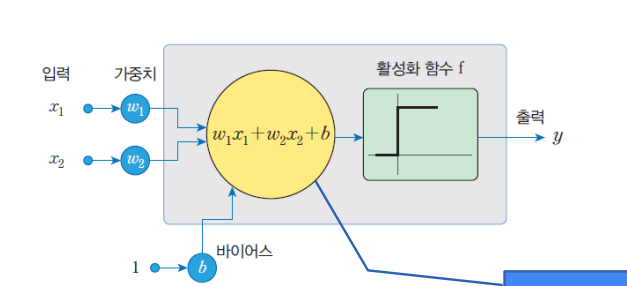
활성화 함수 공식

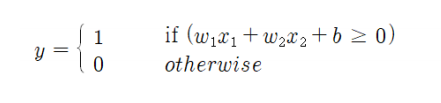
뉴런에서는 입력 신호의 가중치 합이 어떤 임계값을 넘는 경우에만 뉴런이 활성화되어서 1을 출력한다. 그렇지 않으면 0을 출력한다.

연산 예제

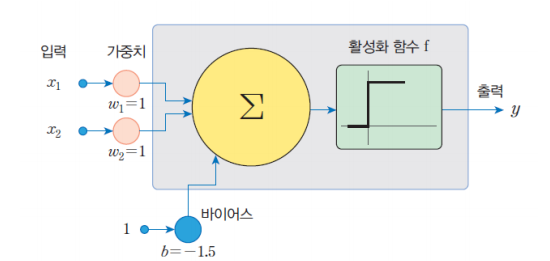
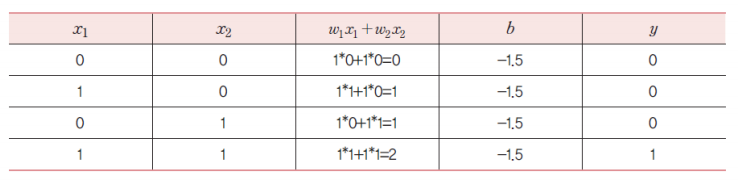
퍼셉트론 학습 알고리즘

학습이라고 부르려면 신경망이 스스로 가중치를 자동으로 설정해주는
알고리즘이 필요하다.
퍼셉트론에서도 학습 알고리즘이 존재한다!

예시

퍼셉트론이 1을 0으로 잘못 식별했다고 하자. 가중치의 변화량은
η (1-0) x_i^k 가 된다. 따라서 가중치는 증가된다.
가중치가 증가되면 출력도 증가되어서 출력이 0에서 1이 될 가능성이 있다.

반대로 0을 1로 잘못 식별했다고 하자. 가중치의 변화량은
η (0-1) x_i^k 가 된다. 따라서 가중치는 줄어든다.
가중치가 줄어들면 출력도 감소되어서 출력이 1에서 0이 될 가능성이 있다.

코드로 구현하면 다음과 같다.

import numpy as np

epsilon = 0.0000001 # 부동소수점 오차 방지

def step_func(t): # 퍼셉트론의 활성화 함수
	if t > epsilon: return 1
    else: return 0

def perceptron_fit(X, Y, epochs=10): # 퍼셉트론 학습 알고리즘 구현

	global W
	eta = 0.2 # 학습률

	for t in range(epochs):
		print("epoch=", t, "======================")
		for i in range(len(X)):
			predict = step_func(np.dot(X[i], W))
			error = Y[i] - predict # 오차 계산
			W += eta * error * X[i] # 가중치 업데이트
			print("현재 처리 입력=",X[i],"정답=",Y[i],"출력=",predict,"변경된 가중치=", W)
		print("================================")
def perceptron_predict(X, Y): # 예측
	global W
	for x in X:
		print(x[0], x[1], "->", step_func(np.dot(x, W)))
        
X = np.array([ # 훈련 데이터 세트
[0, 0, 1], # 맨 끝의 1은 바이어스를 위한 입력 신호 1이다. 
[0, 1, 1], 
[1, 0, 1], 
[1, 1, 1] 
])

y = np.array([0, 0, 0, 1]) # 정답을 저장하는 넘파이 행렬
W = np.zeros(len(X[0])) # 가중치를 저장하는 넘파이 행렬

perceptron_fit(X, y, 6)
perceptron_predict(X, y)

출력 결과

epoch= 0 ======================
현재 처리 입력= [0 0 1] 정답= 0 출력= 0 변경된 가중치= [0. 0. 0.]
현재 처리 입력= [0 1 1] 정답= 0 출력= 0 변경된 가중치= [0. 0. 0.]
현재 처리 입력= [1 0 1] 정답= 0 출력= 0 변경된 가중치= [0. 0. 0.]
현재 처리 입력= [1 1 1] 정답= 1 출력= 0 변경된 가중치= [0.2 0.2 0.2]
================================
epoch= 1 ======================
현재 처리 입력= [0 0 1] 정답= 0 출력= 1 변경된 가중치= [0.2 0.2 0. ]
현재 처리 입력= [0 1 1] 정답= 0 출력= 1 변경된 가중치= [ 0.2 0. -0.2]
현재 처리 입력= [1 0 1] 정답= 0 출력= 0 변경된 가중치= [ 0.2 0. -0.2]
현재 처리 입력= [1 1 1] 정답= 1 출력= 0 변경된 가중치= [0.4 0.2 0. ]
================================
epoch= 2 ======================
현재 처리 입력= [0 0 1] 정답= 0 출력= 0 변경된 가중치= [0.4 0.2 0. ]
현재 처리 입력= [0 1 1] 정답= 0 출력= 1 변경된 가중치= [ 0.4 0. -0.2]
현재 처리 입력= [1 0 1] 정답= 0 출력= 1 변경된 가중치= [ 0.2 0. -0.4]
현재 처리 입력= [1 1 1] 정답= 1 출력= 0 변경된 가중치= [ 0.4 0.2 -0.2]
================================
epoch= 3 ======================
현재 처리 입력= [0 0 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.2 -0.2]
현재 처리 입력= [0 1 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.2 -0.2]
현재 처리 입력= [1 0 1] 정답= 0 출력= 1 변경된 가중치= [ 0.2 0.2 -0.4]
현재 처리 입력= [1 1 1] 정답= 1 출력= 0 변경된 가중치= [ 0.4 0.4 -0.2]
================================
epoch= 4 ======================
현재 처리 입력= [0 0 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.4 -0.2]
현재 처리 입력= [0 1 1] 정답= 0 출력= 1 변경된 가중치= [ 0.4 0.2 -0.4]
현재 처리 입력= [1 0 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.2 -0.4]
현재 처리 입력= [1 1 1] 정답= 1 출력= 1 변경된 가중치= [ 0.4 0.2 -0.4]
================================
epoch= 5 ======================
현재 처리 입력= [0 0 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.2 -0.4]
현재 처리 입력= [0 1 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.2 -0.4]
현재 처리 입력= [1 0 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.2 -0.4]
현재 처리 입력= [1 1 1] 정답= 1 출력= 1 변경된 가중치= [ 0.4 0.2 -0.4]
================================
0 0 -> 0
0 1 -> 0
1 0 -> 0
1 1 -> 1

sklearn을 사용해보자

from sklearn.linear_model import Perceptron 

# 샘플과 레이블이다.
X = [[0,0],[0,1],[1,0],[1,1]]
y = [0, 0, 0, 1]

# 퍼셉트론을 생성한다. tol는 종료 조건이다. random_state는 난수의 시드이다.
clf = Perceptron(tol=1e-3, random_state=0)

# 학습을 수행한다. 
clf.fit(X, y)

# 테스트를 수행한다. 
print(clf.predict(X))

출력 결과

[0 0 0 1]

코드가 매우 간결해졌음을 볼 수 있다.
사실 원리만 알고 있다면 이러한 tool을 적극 활용하는 것이 효율적이다.

퍼셉트론의 한계점

XOR 연산이 불가능하다.

why?

패턴 인식 측면에서 보면 퍼셉트론은 직선을 이용하여 입력 패턴을 분류하는 선형 분류자(linear classifier)의 일종이라고 말할 수 있다.

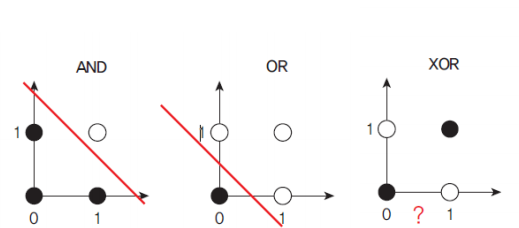
이러한 문제는 다음에 설명할 다층 퍼셉트론으로 해결할 수 있다.