최적화
모델의 손실 함수(Loss Function)를 최소화한다는 의미이다.
경사 하강법(Gradient Descent)
경사 하강법은 손실 함수가 어떤 형태이라도, 또 매개 변수가 아무리 많아도 적용할 수 있는 일반적인 방법이다.
경사를 따라 내려가면서 가중치(w) 업데이트 시킨다.
손실함수를 최소화하기 위하여 반복적으로 파라미터를 조정해나가는 방법이다.
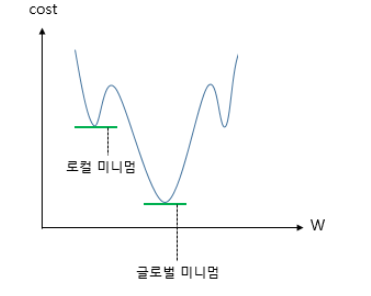
학습률(learning rate)이 너무 크면 학습시간이 짧아지며, 전역 최솟값에서 멀어진다.
학습률(learning rate)이 너무 작으면 학습시간이 길어지며, 지역 최솟값에 수렴한다.
그러므로 적당한 학습률을 넣는 것이 중요하다.
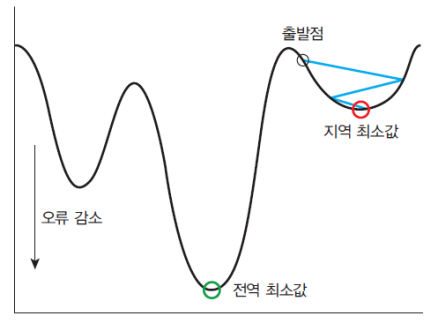
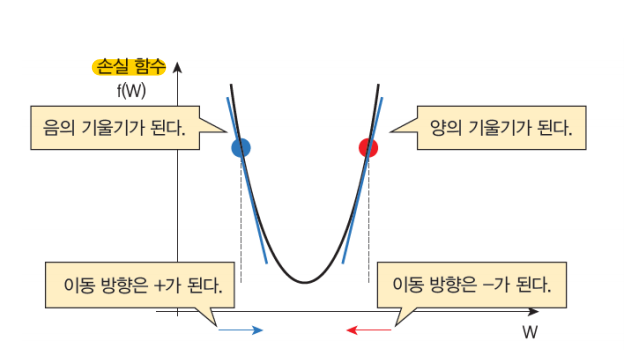
선형 회귀에서의 경사 하강법
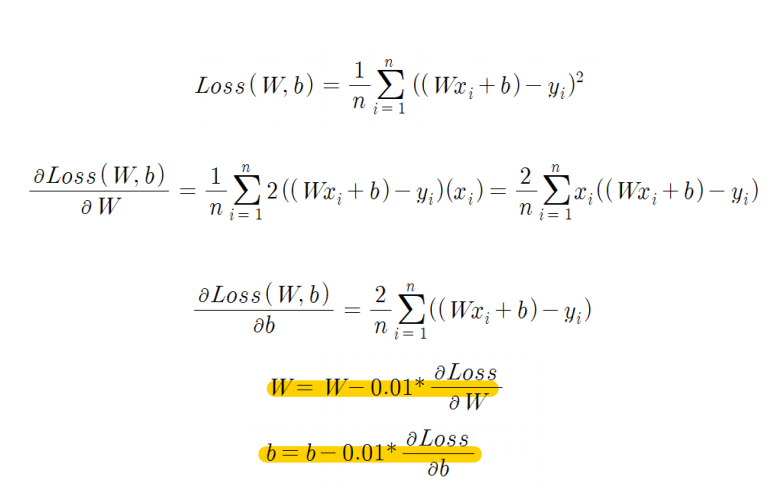
손실함수 공식에서 편향 b와 가중치 w에 대한 편미분을 계산하여
편미분은 비용 함수에 대한 각 파라미터의 변화율을 나타낸다.
0.01은 학습률이며 최종적인 공식은
w = w - learning_rate * (∂MSE/∂w)
b = b - learning_rate * (∂MSE/∂b)
이다.
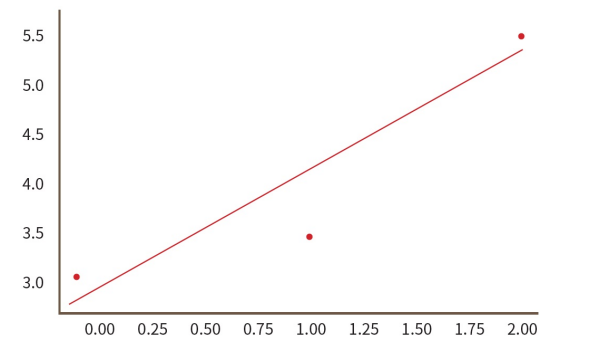
경사하강법 구현


결과

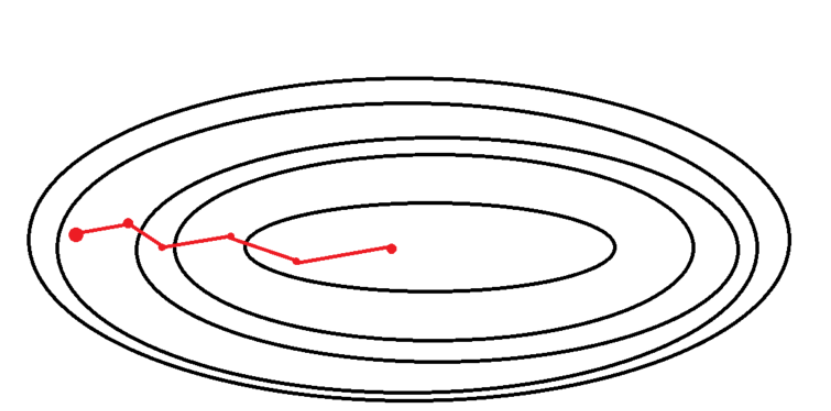
배치 경사 하강법(batch Gradient Descent)
배치란?
주어진 작업을 수행할 때 일괄적으로 처리할 데이터의 양을 나타낸다.
데이터셋을 전부 사용하므로 계산이 안정적이고, 수렴이 보장된다.
단, 큰 데이터셋에서는 메모리와 계산 비용이 높을 수 있다.
전체 데이터에 대한 모델의 오차의 평균을 구한 다음, 이를 이용하여 편미분을 진행한다는 점에서 경사 하강법과 차이가 있다.
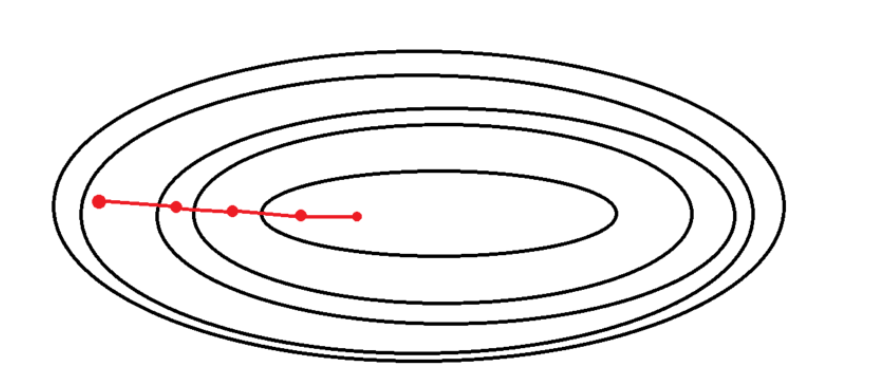
확률적 경사 하강법(Stochastic Gradient Descent, SGD)
확률적으로 선택한 단 하나의 데이터만을 이용해 경사 하강법을 1번 진행한다.(배치 크기 1)
학습하는 데이터가 적으므로, 속도가 빠르다.
각 데이터에 대한 손실값의 기울기가 다르기 때문에, 기울기의 방향이 매번 크게 바뀐다.
수렴에 Shooting이 발생한다.
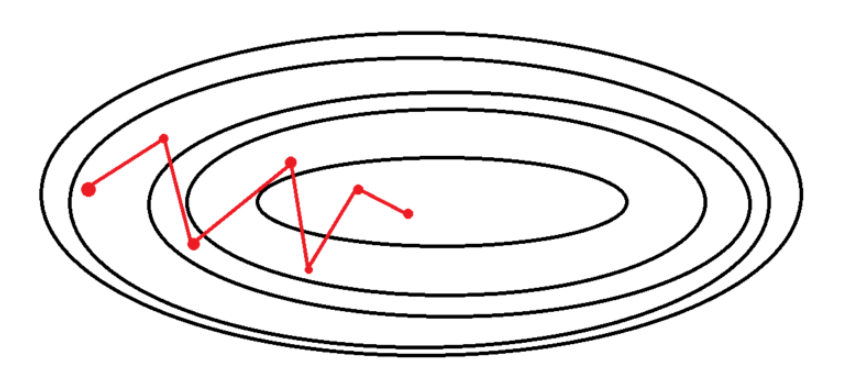
미니 배치 경사 하강법 (Mini-Batch Gradient Descent)
전체 데이터를 batch_size의 크기만큼 나눠 학습한다.
한 배치의 손실값의 평균으로 경사하강을 진행하기 때문에 SDG에 비해 Shooting이 적게 발생한다.
BGD보다 계산량이 적다.
BDG와 SDG의 절충안으로 가장 많이 쓰이는 경사 하강법이다.
모멘텀(Momentum)
관성이라는 물리학 법칙을 응용한 방법
계산된 접선의 기울기에 이전의 접선의 기울기 값을 일정한 비율만큼 반영해 업데이트의 방향을 일정부분 유지한다.
지역 최솟값에 빠져도 관성으로 빠져나올 수 있다.
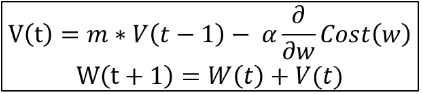
m은 모멘텀 상수로, 일반적으로 0.9이다.
알파는 학습률이고, 그 뒷부분은 현재의 기울기이다.
v(t)는 이전 그레디언트 업데이트의 모멘텀이다.
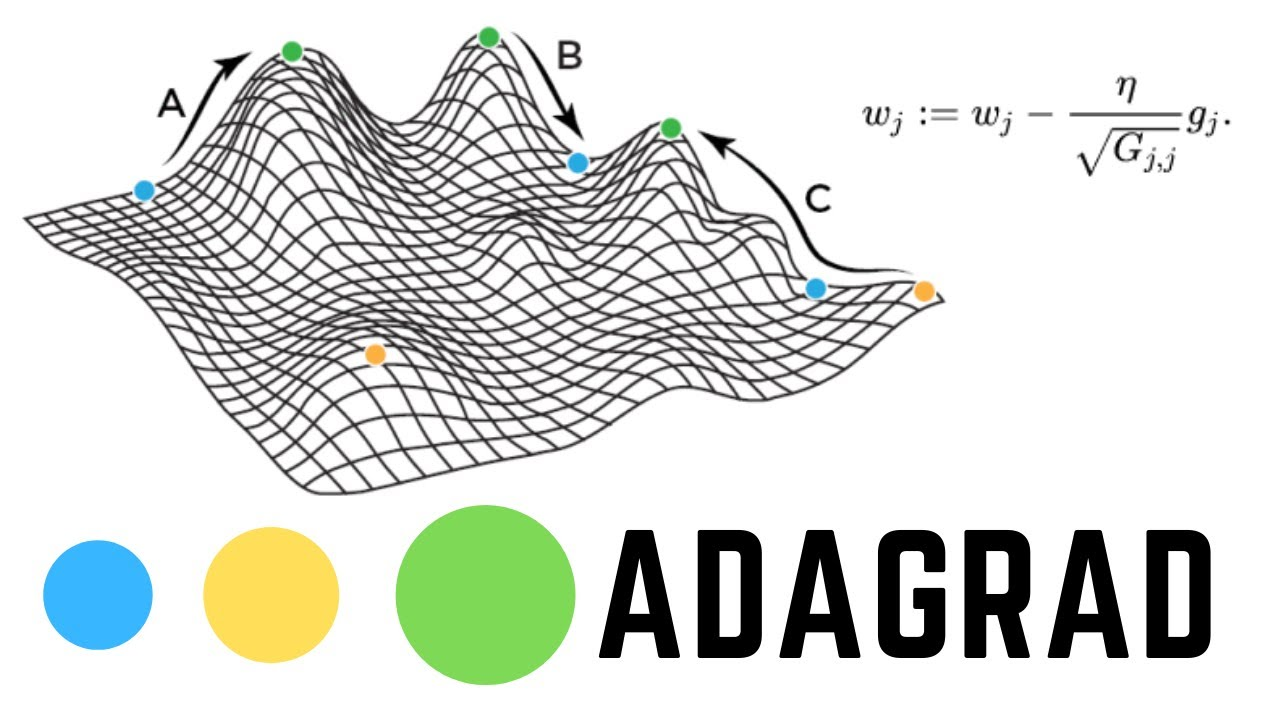
아다그라드(Adagrad[Adaptive Gradient])
가중치 벡터의 업데이트 횟수에 따라 학습률(Learning rate)를 조절하는 옵션이 추가되었다.
많이 변화하지 않은 변수들은 학습률을 크게하고, 반대로 많이 변화한 변수들에 대해서는 학습률을 적게한다.
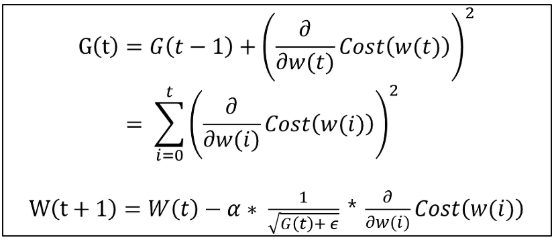
각 단계의 모든 편미분값(그래디언트)의 제곱값들의 합을 더한다.
G(t)가 가중치 벡터에 적용될 때는 학습률을 곱하고, 입실론(아주 작은 상수)을 더한다(0으로 나눠지는 것을 방지하기 위해).
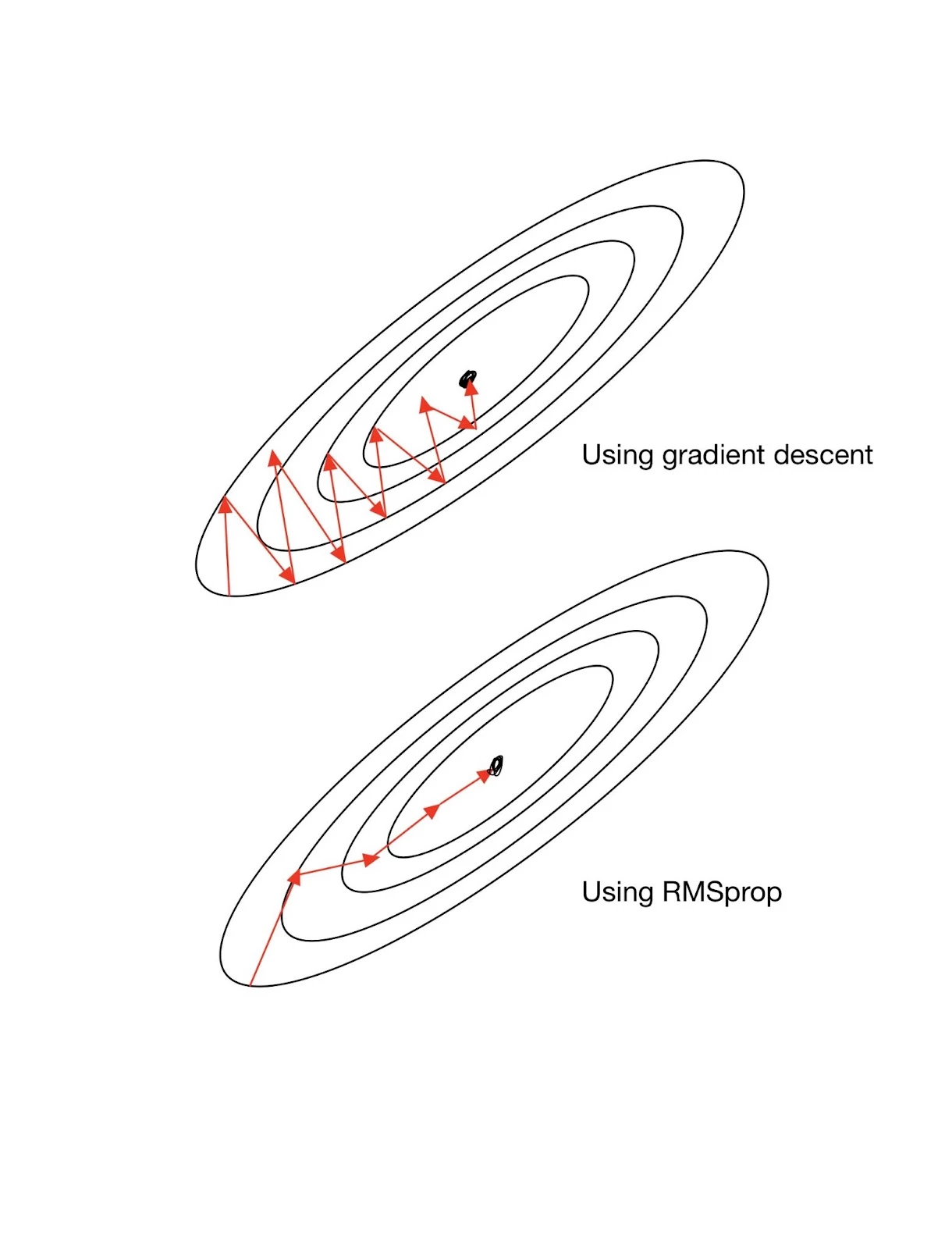
RMSprop
아다그라드의 G(t)의 값이 무한히 커지는 것을 방지하고자 제안된 방법이다.
아담(Adam)
RMSprop의 특징인 편미분의 제곱을 지수평균한 값을 사용한다.
모멘텀의 특징으로 편미분을 제곱하지 않은 값을 사용하여 지수평균을 구하고 수식에 활용한다.
아다델타(AdaDelta[Adaptive Delta])
Adagrad, RMSprop, Momentum 모두를 합친 경사하강법이다.
이 방법은 이해가 도저히 안 된다....
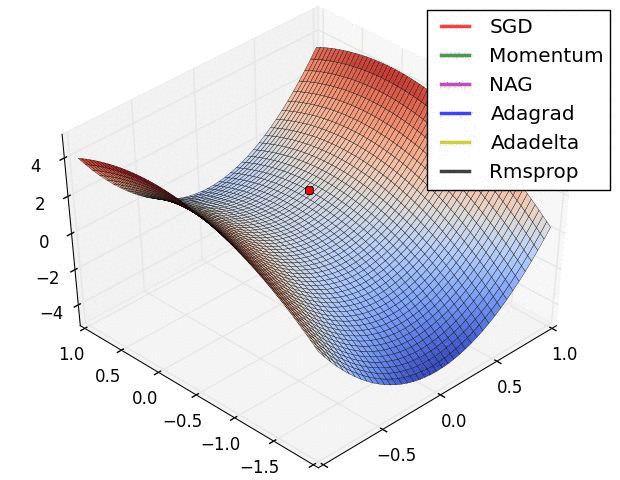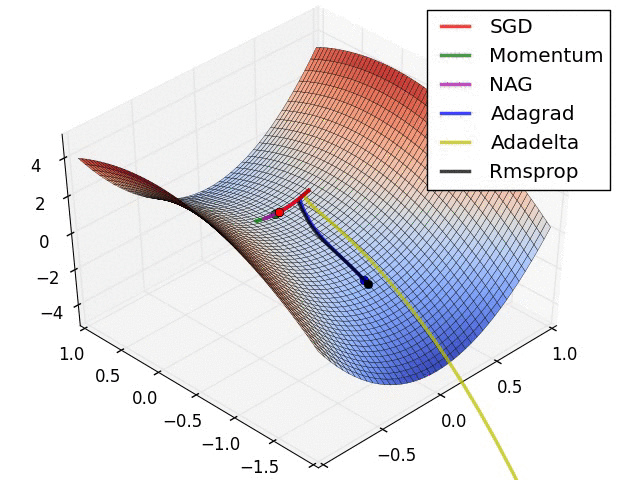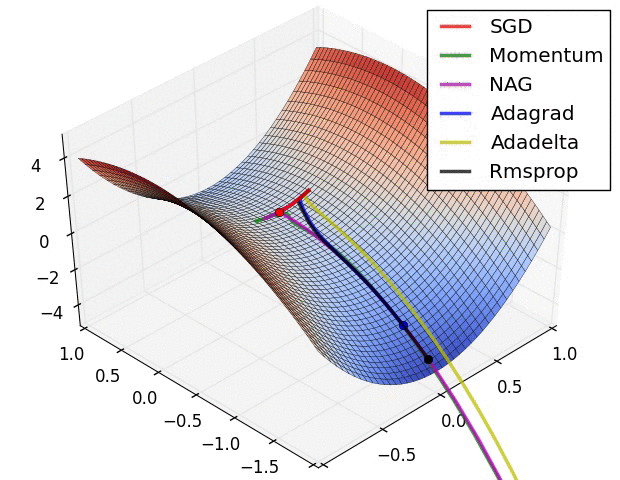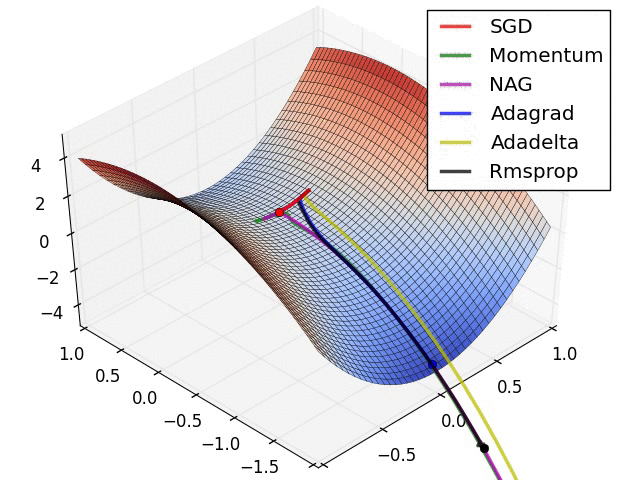
Adadelta가 최적화를 가장 잘하는 모습을 보이고 있다.
