Polynomial Feature Function
-
원래의 특성들을 조합하여 고차원의 특성을 생성합니다. 예를 들어, 두 특성 가 있을 때, 2차 다항식 특성으로는 가 생성될 수 있습니다.
-
이렇게 생성된 고차원 특성은 원래 데이터의 비선형 관계를 포착하는 데 도움을 줍니다. 선형 모델은 원래 선형 관계만을 모델링할 수 있지만, 다항식 특성을 사용하면 비선형 관계도 효과적으로 나타낼 수 있습니다.
-
주의사항
- Overfitting의 위험 : 다항식 특성을 추가하면 모델의 복잡도가 증가하므로 Overfitting의 위험이 커질 수 있습니다. 적절한 차수의 다항식을 선택하고, 교차 검증 등을 사용하여 과적합을 방지해야 합니다.
- Scaling의 중요성 : 다항식 특성은 값의 범위가 크게 달라질 수 있으므로, feature의 스케일링이 중요합니다. 특성의 scale을 조정함으로써 모델의 학습 성능과 안정성을 높일 수 있습니다.
Regularization
- Data points에 비해 parameter 수가 많으면 overfitting의 위험이 있을 수 있습니다.
- Model이 너무 복잡해서 Overfitting이 발생하였다면, 몇몇의 불필요한 input을 제거하면서 정확도를 상승시킬 수 있습니다.
- 일부 계수를 0으로 설정하면 예측 정확도를 향상시킬 수 있습니다.
- 이렇게 함으로써 모델을 Simple하게 만들 수 있습니다.
- Gradient descent + automatically yields simpler model이라고 볼 수 있다.
- 무엇보다 중요한 것은 X와 Y의 값은 0-1 사이의 값으로 Normalization 해야합니다. 왜냐하면 각 독립변수들을 표준화하여 평균이 0이고 분산은 1이 되도록 해야 합니다.
Cost function(L2 - Ridge Regression)
MSE + Ridge(L2 penalty term)
Goal : 를 최소화하는 동시에 도 작게 만들어야 합니다.
-
Overfitting 방지 : 높은 가중치는 데이터의 작은 변화에 모델이 과도하게 반응하는 경향을 나타낼 수 있습니다. 그래서 가중치를 작게 유지함으로써, 모델은 덜 복잡해지고 과적합의 위험이 감소합니다.
-
모델의 간결성 및 해석 용이성 : 가중치가 작으면 모델이 더 간결해지고 해석하기 쉬워집니다. 큰 가중치는 데이터의 특정 특성이 결과에 불균형적으로 큰 영향을 미치는 것을 나타내며, 이는 모델의 해석을 어렵게 만듭니다.
-
수치적 안정성 : 높은 가중치는 수치적 불안정성을 초래할 수 있습니다. 예를 들어, 매우 큰 가중치는 입력 데이터의 작은 변화에 예측 결과가 크게 바뀔 수 있습니다. 작은 가중치는 이러한 민감성을 줄이고 모델의 예측을 더 안정적으로 만듭니다.
-
특성 간의 균형 : L2 Regularization은 모든 가중치를 동시에 축소시키므로, 모델이 모든 특성을 고르게 고려하도록 유도합니다. 즉, 모든 가중치가 비슷한 수준으로 축소되도록 합니다. 큰 가중치는 더 큰 패널티를 받고, 작은 가중치는 더 작은 패널티를 받습니다. 이는 모델이 몇몇 특성에 지나치게 의존하는 것을 방지하고, 보다 균형 잡힌 학습을 촉진합니다.
-
Ridge regression에서는 가중치의 제곱합을 최소화하는 것이 매우 중요합니다.
Cost function(L1 - Lasso Regression)
가 커질수록 모델은 더 simple해지고(Underfitting), 가 작아지면 모델은 더 복잡해집니다(Overfitting).
Ridge vs Lasso
- Lasso가 Ridge에 비해서 가중치를 0으로 만듭니다.
- Ridge는 불필요한 즉, 0과 가깝게 만들어줍니다. 0이 아니라.
- 반면, Lasso는 불필요한 으로 만들어줍니다.
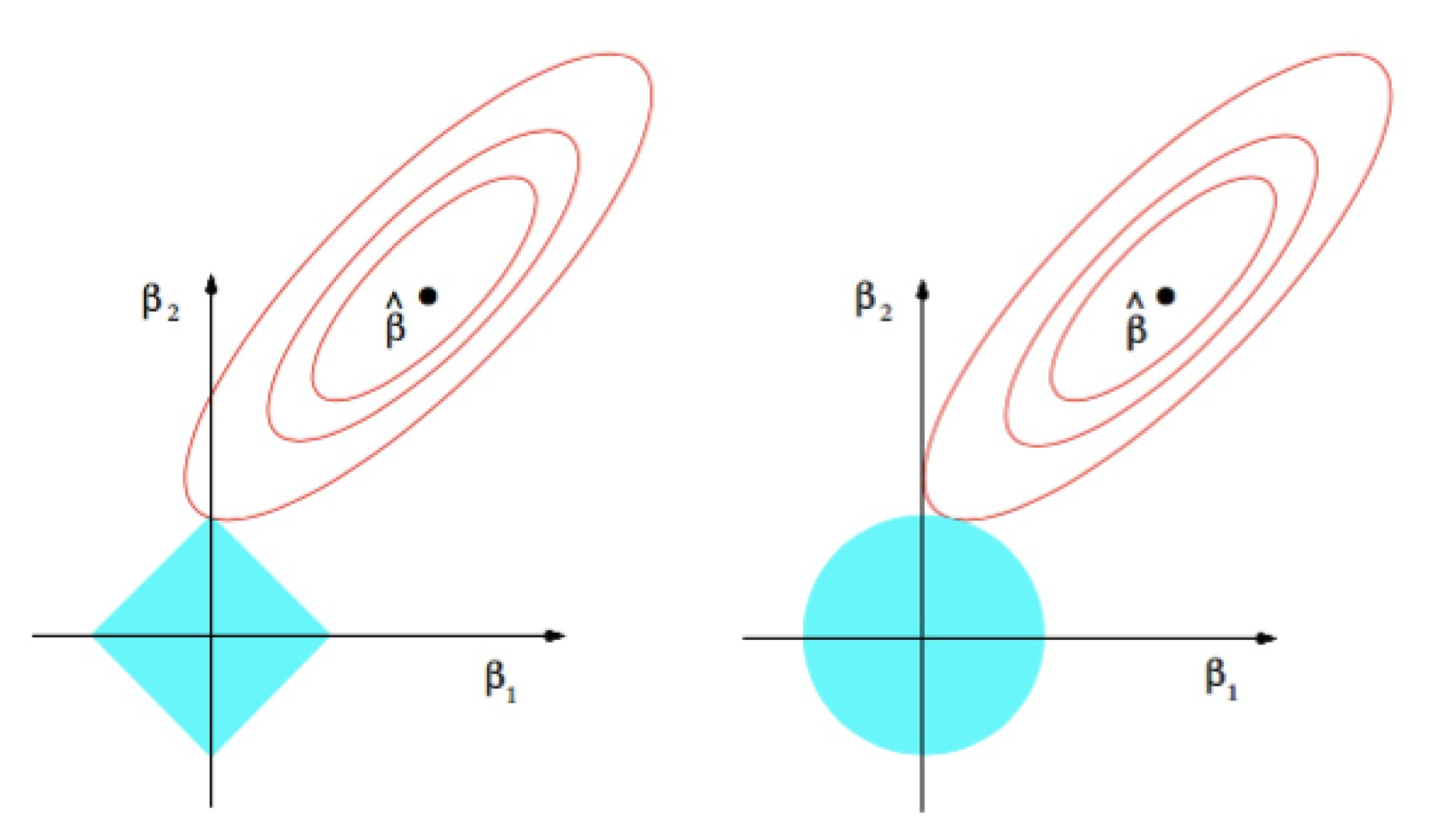
- 결국, 불필요한 w를 꺼버리면서, MSE는 살짝 높아질 수 있는 데 이것이 Regularization의 효과라고 볼 수 있습니다.
