📌 Are Graph Augmentations Necessary? Simple Graph Contrastive Learning for Recommendation

📖 ABSTRACT

1. Contrastive Learning이 더 고르게 분포된 사용자/아이템 표현을 학습하여 인기 편향을 완화시키는 방식임을 실험적으로 보인다.

2. 필요하다고 여겨졌던 그래프 증강이 사실 미미한 역할임을 밝히고, 이를 대신해 임베딩 공간에 균일한 노이즈를 추가하는 간단한 CL 방법을 제안한다.

📖 INTRODUCTION

Contrastive learning은 raw data에서 자가 지도 신호를 추출하여 학습하기 때문에 추천 분야에서 데이터 희소성 문제의 해결책으로 대두되고 있다.

아래 그림은 CL 기반 추천 모델 SGL의 파이프라인이다.

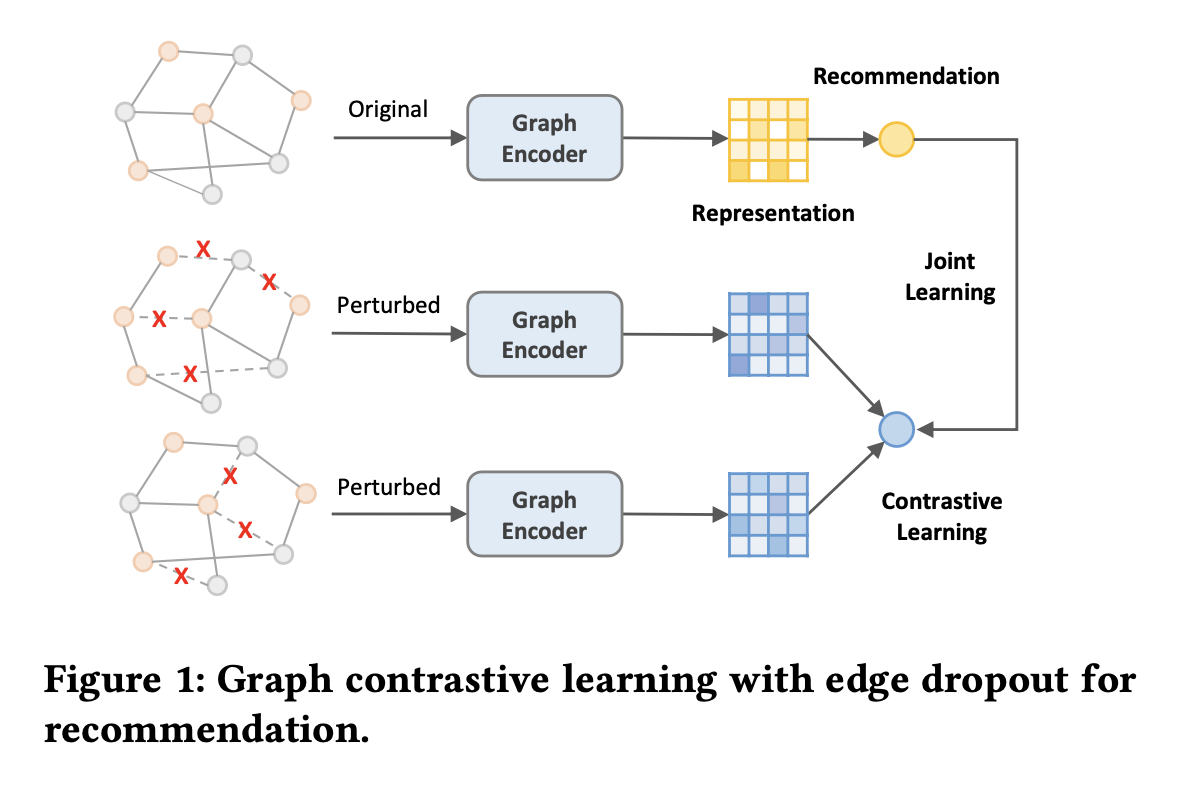
사용자-아이템 이분 그래프를 구조적 변형(에지/노드 드롭아웃)으로 확장한 다음,
동일한 노드에서 변형된 두 그래프 노드 표현의 일관성을 최대화한다.

하지만 본 논문은 지금까지의 연구들이 Contrastive learning을 활용함으로써 얻게된 성능 향상의 근본적인 원리를 명확히 파악하지 못하고 있음을 지적한다.

본래는 에지/노드 드롭아웃을 통해 중복과 불순물을 무작위로 제거함으로써 다양한 그래프 변형을 대조 학습하여 사용자-아이템 상호 작용에서 존재하는 본질적인 정보를 캡처할 수 있다고 가정했다.

하지만 BUIR와 같은 몇몇 연구에서 데이터 증강 시 노드/에지 드롭아웃의 비율을 0.9로 설정한, 극도로 희소하게 만들어져 본래 정보의 큰 손실을 일으킨 그래프 증강에서조차도 성능 향상을 가져올 수 있음을 보임으로써 위 가정을 의심하기 시작한다.

이에 따라 본 논문은 다음과 같은 질문을 던진다.

Contrastive learning을 추천과 통합할 때 정말로 그래프 증강이 필요한가?

이를 확인하기 위해 그래프 증강을 했을 경우와 하지 않았을 경우의 성능을 각각 비교하여 두 경우의 성능이 비슷함을 실험적으로 보인다.

또한 CL이 적용되지 않은 추천 방법과 CL 기반 추천 방법에서 학습된 임베딩 공간을 조사한다.
표현의 분포를 시각화하고 그것들을 성능과 연결시켜봄으로써 추천 성능에 실제로 중요한 것은 그래프 증강이 아니라 CL 손실임을 밝힌다.

한편 올바르게 증강된 데이터는 방해 요소에 대해 불변한 표현을 학습하는 데 도움이 되기 때문에 그래프 증강이 기대만큼 효과적이지는 않지만, 완전히 쓸모 없지 않음을 말한다.

[참고] 불변성(invariance)
불변성이란 어떤 변화에 대해 변하지 않는 특성이나 속성을 의미함으로 강건성과 비슷한 의미를 나타내는 것으로 보인다.
이에 따라 위 맥락에서는 데이터 증강을 통해 모델이 입력 데이터에 민감하지 않고 일정한 성능을 유지할 수 있도록 도와준다는 의미로 해석된다.

그럼에도 그래프 증강에는 다음의 몇가지 한계점을 지적하며 또 다른 질문을 던진다.

1. 훈련 중에 그래프 인접 행렬을 계속 재구성해야 하므로 시간이 많이 소요된다.
2. 엣지/노드 드롭아웃을 통해 증강된 그래프들이 원본 그래프와 일정한 유사성을 유지하기 힘들 수 있다.

더 효과적이고 효율적인 증강 방법이 있을까?

본 논문에서는 표현 분포의 균일성이 핵심 요소임을 발견한 바에 따라, 균일성을 더욱 제어할 수 있으면서 그래프 증강이 없는 CL 방법을 제안한다.
본 논문에서 제안하는 방법은 앞서 언급한 SGL 모델의 프레임워크를 따르지만, 드롭아웃 기반의 그래프 증강을 버리는 대신 원본 표현에 무작위 균일한 잡음을 추가하여 표현 수준의 데이터 증강을 수행한다.

이는 서로 다른 무작위 잡음을 부여함으로써 대조적인 시각 간에 분산을 만들어내면서도, 제어된 크기 때문에 학습 가능한 불변성을 여전히 유지한다.
그래프 증강과 비교하면 제안된 버전은 임베딩 공간을 더 균일한 분포로 직접 규제하며, 구현이 간편하고 효율적임을 보인다.

📖 INVESTIGATION OF GRAPH CONTRASTIVE LEARNING IN RECOMMENDATION

본 섹션에서는 앞서 던진 질문들의 답에 대한 실험적 입증을 보인다.

Necessity of Graph Augmentation

CL 기반의 추천 방법이 어떻게 작동하는지 풀어내기 위해 먼저 SGL에서 그래프 증강의 필요성을 조사한다.
다음 표는 기존 SGL 모델들과 SGL에서 증강을 없앤 새로운 변형 SGL-WA를 만들어 성능을 비교한 결과를 보인다.

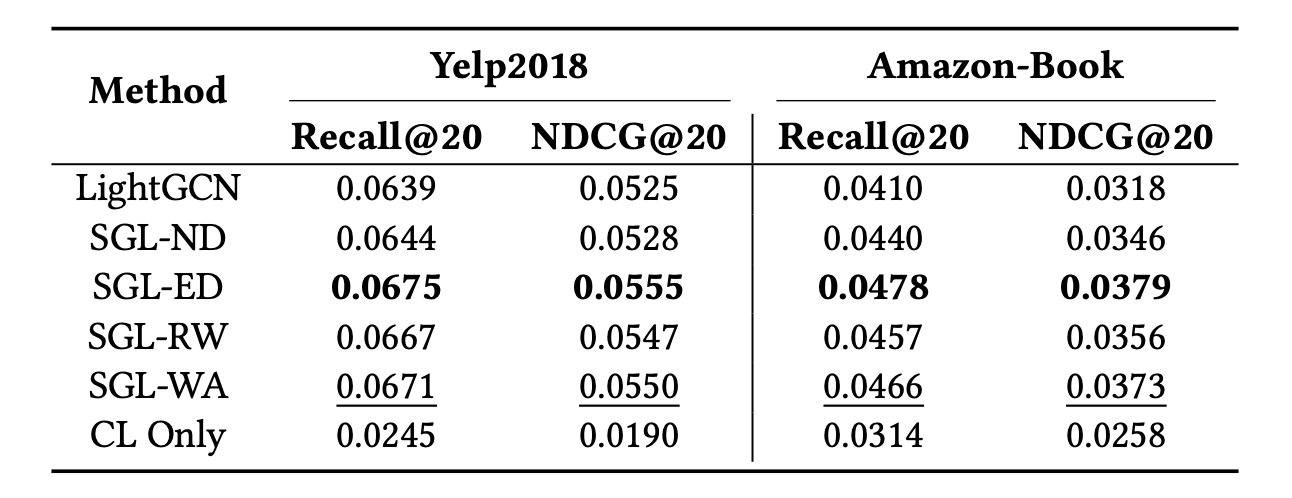
1. SGL의 모든 변형은 LightGCN의 성능을 큰 폭으로 앞선다.
2. SGL-WA은 그래프 증강이 분리되었음에도 SGL-ND 및 SGL-RW보다 뛰어난 성능을 보인다. 이에 노드 드롭아웃과 무작위 워크가 핵심 노드와 관련된 엣지를 삭제하여 본래 그래프를 심하게 왜곡시킬 가능성이 매우 높아 이러한 결과를 만들어낸다고 추측하여 말한다.
3. SGL-ED가 SGL-WA보다 높은 성능을 유지하고 있음을 보인다. 이에 일회성 에지 드롭아웃은 본래 그래프를 크게 교란시키지 않을 가능성이 높기 때문에 이러한 결과를 가져왔다고 추측하여 말한다.

그럼에도 본 논문은 앞서 말했듯이 다음의 한계점을 고려하여 그래프 증강의 필요성을 다시 생각해봐야 한다고 주장한다.

1. 훈련 중에 그래프 인접 행렬을 계속 재구성해야 하므로 시간이 많이 소요된다.
2. 엣지/노드 드롭아웃을 통해 증강된 그래프들이 원본 그래프와 일정한 유사성을 유지하기 힘들 수 있다.

InfoNCE Loss Influences More

또 다른 논문은 Contrastive loss를 최적화하면 시각적 표현 학습에서 다음 두 가지 특성이 강화된다고 말한다.
1. 양성 쌍에 속하는 비슷한 샘플들간의 특징이 서로 가깝게 정렬된다.
2. hypersphere에서 정규화된 특징 분포가 균일성을 보인다.

본 논문은 이에 따라 두 번째 특성 균일성에 대해 조사한다.

먼저 학습된 표현을 t-SNE를 사용하여 hypersphere에 있는 2차원 정규화된 벡터로 매핑한다.
그런 다음 비모수적인 가우시안 커널 밀도 추정을 사용하여 특징 분포를 플로팅 한 결과로 다음의 그림을 보인다.

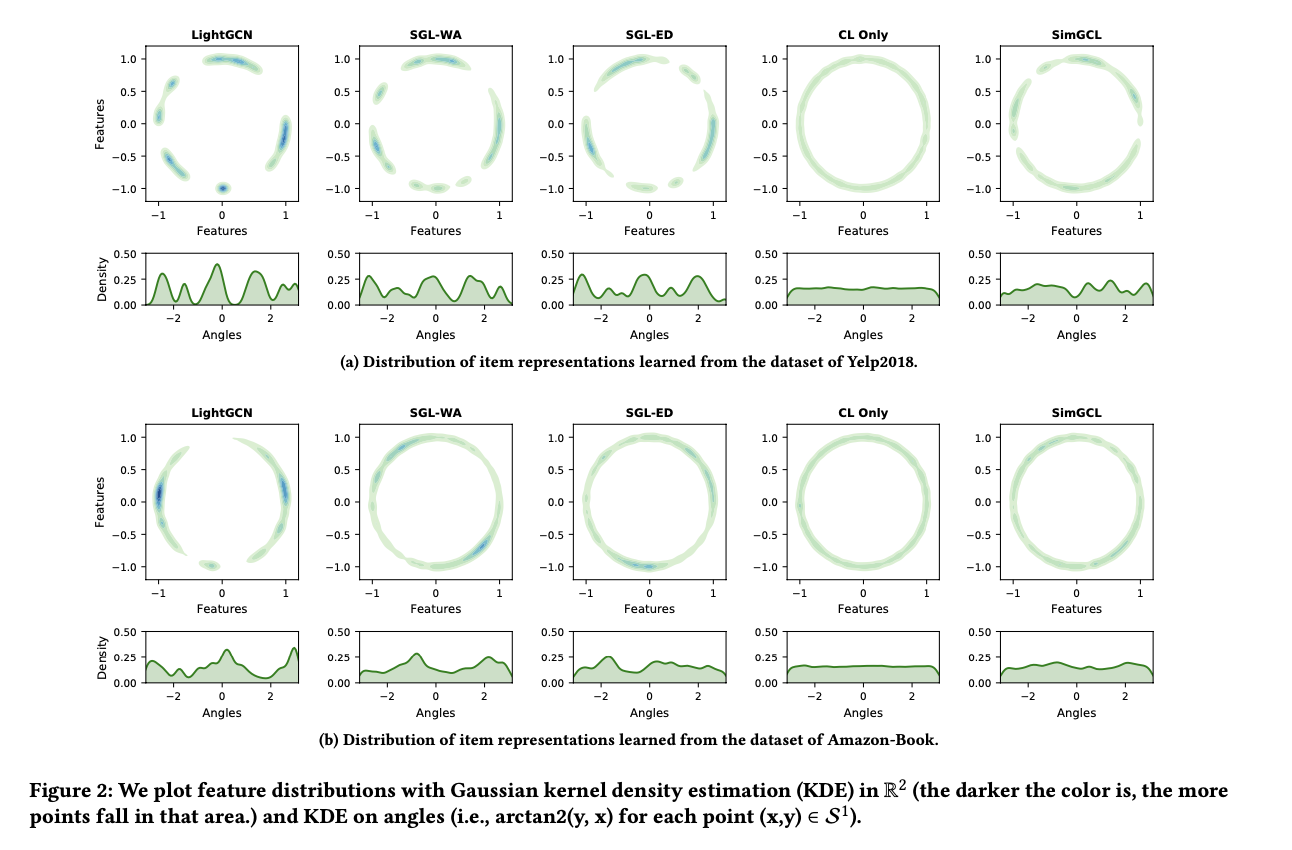
1. 가장 왼쪽 열의 LightGCN은 매우 군집된 특징을 보인다.
2. 다음 두 번째와 세 번째 열에서는 분포가 더 균일해지고 밀도 추정 곡선이 보다 부드러워졌다. 이는 그래프 증강이 적용되었는지 여부에 상관없이 변화가 나타났다.
3. 네 번째 열에서는 대비 손실로만 학습된 특징을 플로팅하며, 분포가 거의 완전하게 균일함을 보인다.

특징의 분포가 높게 군집되는 이유로 다음 두 가지를 언급한다.

1. LightGCN의 메시지 패싱 메커니즘으로 인해 레이어가 증가함에 따라 노드 임베딩이 지역적으로 유사해진다.
2. 추천 데이터는 일반적으로 롱테일 분포를 따르기 때문에 많은 상호 작용을 가진 인기 아이템이 각 사용자 임베딩에 영향을 많이 미치게됨에 따라 임베딩이 유사해진다.

최종적으로 앞서 소개한 표 1과 그림 2의 분포를 함께 고려함에 따라, 분포의 균일성이 SGL에서 추천 성능에 결정적인 영향을 미치는 근본적인 요소라는 결론을 얻는다.

또한 CL 손실만을 최소화하면 낮은 성능이 나타나는 것을 통해 균일성과 성능 사이에 긍정적인 상관 관계가 일정 범위에서만 성립한다는 것을 알 수 있다.
균일성을 지나치게 추구하면 상호 작용하는 쌍과 유사한 사용자/아이템의 근접성을 간과하여 추천 성능을 저해할 수 있기 때문이다.

📖 SIMGCL: SIMPLE GRAPH CONTRASTIVE LEARNING FOR RECOMMENDATION

위 결과에 따라 본 섹션에서는 균일성을 원활하게 조절하고 CL의 이점을 최대화하는 추천 방법 SimGCL을 제안한다.

Motivation and Formulation

SimGCL은 그래프 구조를 조작하여 표현 공간을 더 균일하게 만드는 것은 복잡하고 시간이 많이 소요되기 때문에 임베딩 공간에서 표현에 직접 무작위 잡음을 추가한다.

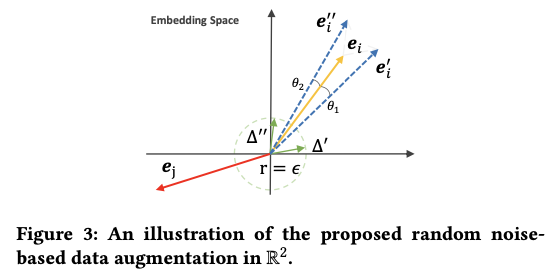
노드 $i$와 그에 대한 표현 $e_i$가 있는 $d$-차원 임베딩 공간이 주어졌을 때, 다음과 같이 표현 수준의 증강을 나타낸다.

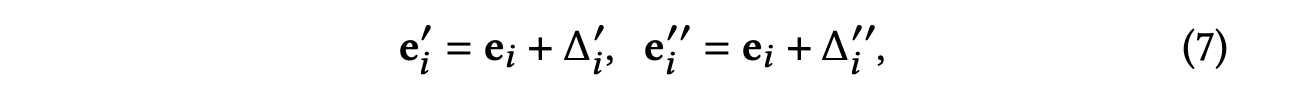
추가된 노이즈 벡터 $△'$와 $△''$는 다음 두 가지 제약을 따른다.

1. $△$는 수치적으로 반지름이 $ε$인 hypersphere의 점과 동일하다.
2. $△'$와 $△''$는 동일한 hyperoctant에 있어야 하므로 노이즈를 추가해도 $e_i$의 큰 편차를 초래하지 않는다.

다음 그림은 위 과정을 잘 나타낸다.

본래 표현에 스케일 조절된 노이즈 벡터를 추가함으로써 $e_i$를 작은 각도 $θ_1$와 $θ_2$만큼 회전시킨다.
각 회전은 $e_i$의 편차에 해당하며, 증강된 표현 $e_i'$와 $e_i''$가 된다.

회전이 충분히 작기 때문에 증강된 표현은 원래 표현의 대부분 정보를 보존하면서 동시에 일부 분산도 유지한다.
추가적으로 각 노드 표현에 대해 추가되는 무작위 노이즈는 각자 다르다.

SGL을 따라 SimSGL 또한 LightGCN을 그래프 인코더로 사용한다.
각 레이어에서 현재 노드 임베딩에 다르게 스케일 조절된 무작위 노이즈가 더해져 다음의 과정으로 노드 표현이 학습된다.

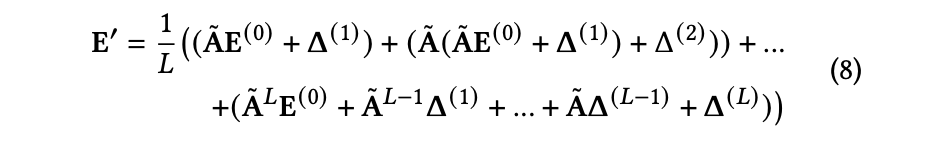
Regulating Uniformity

SimGCL에서 두 개의 하이퍼파라미터 λ와 $ε$는 표현의 균일성에 영향을 미칠 수 있다.
그 중 ε의 값을 조절하는 것이 λ을 조절하는 것보다 더 명시적이고 원활하게 균일성을 만들 수 있으며, 이에 대해서는 아래 실험적으로 입증함을 보인다.
따라서 본 섹션에서는 ε를 조정하여 균일성이 어떻게 변하는지 관찰한다.

표현의 균일성을 측정하기 위한 메트릭으로 평균 쌍별 가우시안 포텐셜의 로그를 사용한다.

이 메트릭은 데이터 표현의 균일성을 측정하기 위해 사용되며, 높은 값은 표현이 덜 균일하다는 것을 나타내며, 낮은 값은 더 균일한 표현을 나타낸다.

다음 그림은 각 ε의 값을 적용한 모델들이 모두 최적의 솔루션으로 수렴하는 동안 처음 30 에포크 동안 값의 기록을 보인다.

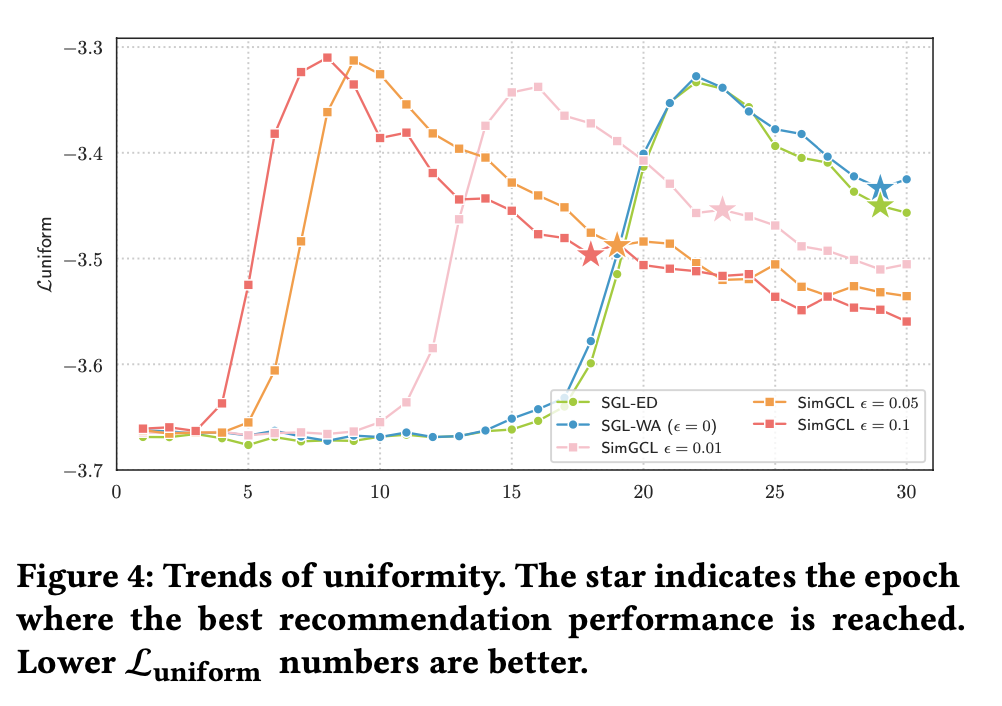
결과적으로 모든 곡선에서 유사한 경향을 보인다.
초기 단계에서 모든 방법은 Xavir 초기화를 사용했기 때문에 표현이 매우 균일하게 분포되어 있으며, 훈련이 진행됨에 따라 균일성이 감소하고, 최고점에 도달한 후 균일성이 수렴할 때까지 향상된다.

SimGCL의 경우 ε가 증가함에 따라 더 균일한 표현을 학습하는 경향이 있으며, 매우 작은 ε조차도 SGL 변형과 비교했을 때 더 높은 균일성을 보인다.

이러한 결과들은 그래프 증강을 노이즈 기반 증강으로 대체함으로써 SimGCL이 학습된 표현의 균일성을 제어하는 데 더 능숙하며 편향을 줄일 수 있다는 주장을 지지한다.

📖 EXPERIMENTAL RESULTS

SGL vs. SimGCL: From a Comprehensive Perspective

Performance Comparison

다음 표는 세 가지 데이터셋에서 SGL과 SimGCL의 성능을 비교한 결과이다.

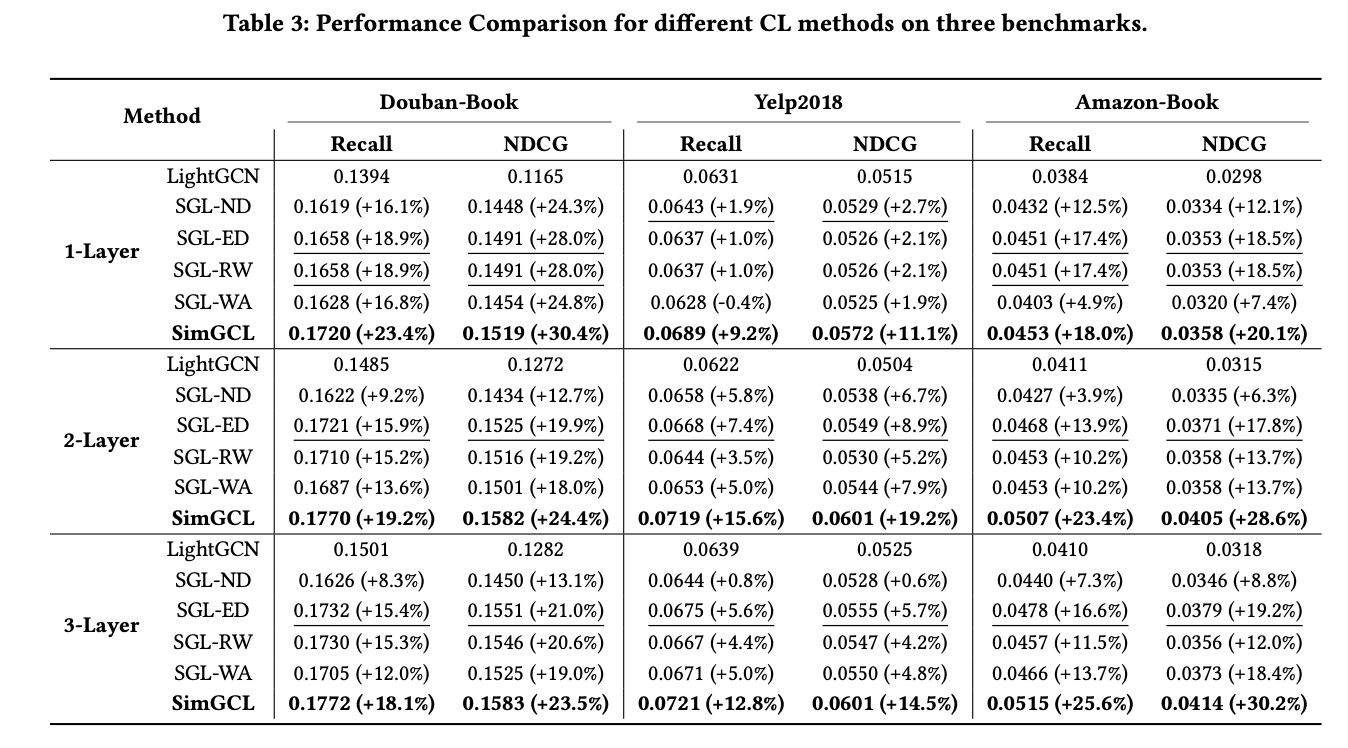
SimGCL은 모든 경우에서 가장 우수한 성능을 보이며, 이는 무작위 노이즈 기반 데이터 증강의 효과를 입증한다.

Convergence Speed Comparison

다음 표는 세 가지 데이터셋에서 SGL과 SimGCL의 수렴 속도를 비교한 결과이다.

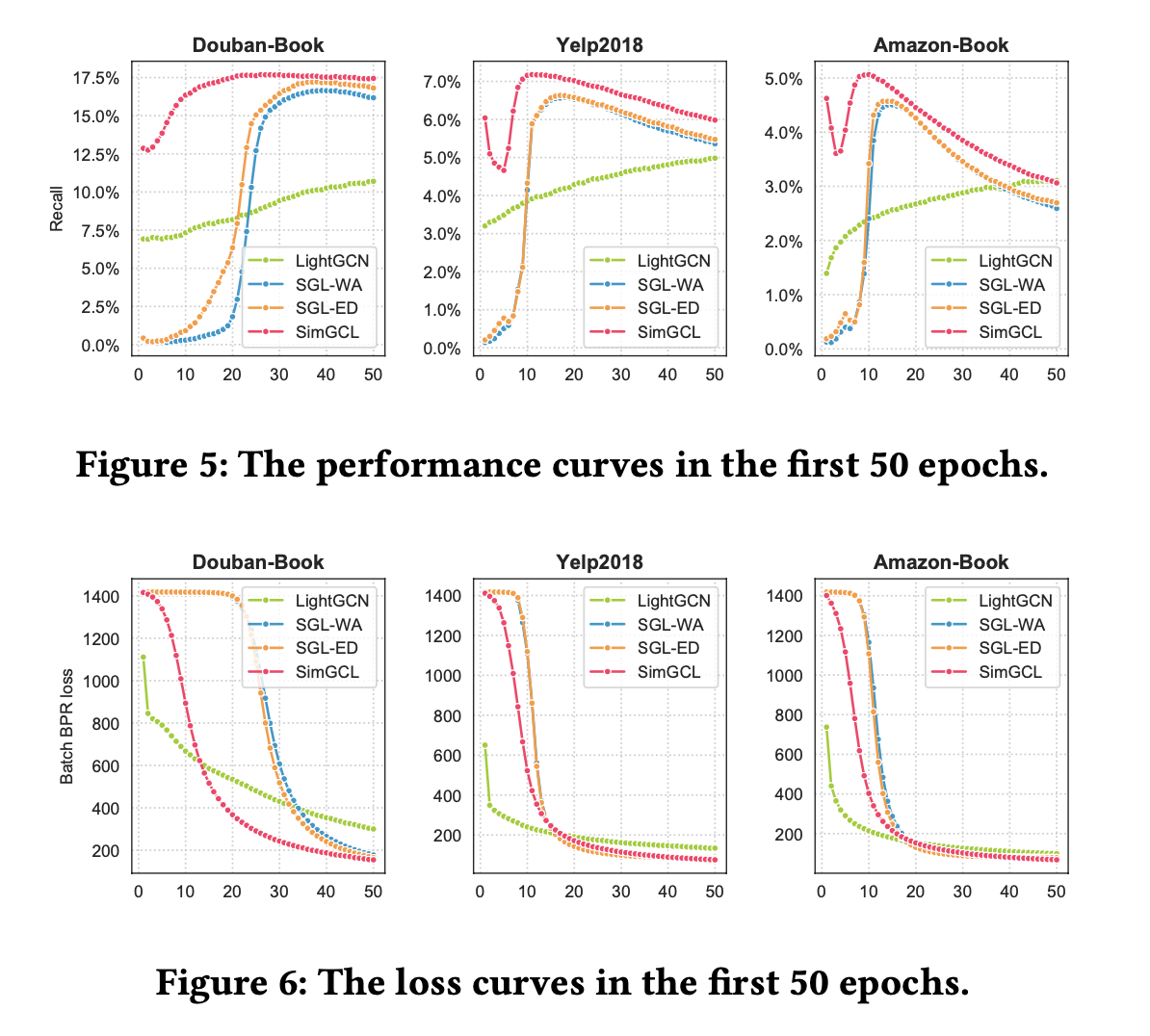
SimGCL은 모든 경우에서 가장 빠른 수렴 속도를 보인다.
SimGCL은 각 테스트 세트에서 최상의 성능을 25번째, 11번째 그리고 10번째 에포크에 도달하는 반면,
SGL-DE는 각각 38번째, 17번째 그리고 14번째 에포크에 정점에 도달한다고 한다.

추가로 SGL 논문에서는 CL 손실에서의 다양한 부정적인 예가 빠른 수렴에 기여할 수 있다고 말하지만, SGL-ED의 수렴 속도는 증강을 하지 않는 SGL-WA와 거의 동등한 성능을 보인다는 것을 알 수 있다.

Running Time Comparison

다음 표는 한 번의 에포크에 소요하는 실행 시간을 나타낸다.

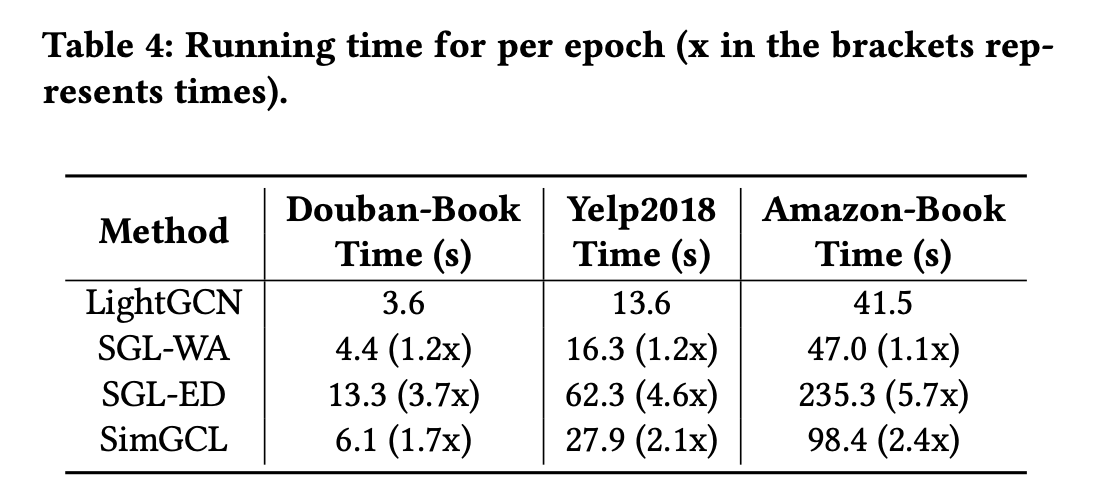
앞서 실험의 SimGCL이 SGL-ED가 소비하는 에포크의 2/3만 필요하다는 것을 고려할 때, 효율성 측면에서 SimGCL이 뛰어난 성능을 보인다는 것을 알 수 있다.

Ability to Debias

앞서 infoNCE loss는 더 균일한 표현을 학습함으로써 인기 편향 문제를 완화시킬 수 있는 능력이 있음을 보였다.
다음 그림은 SimGCL이 이러한 능력을 향상시키는지 확인하기 위해 테스트 세트를 아이템의 인기에 비례하여 세 부분으로 나누어 실험을 진행한 결과를 보인다.

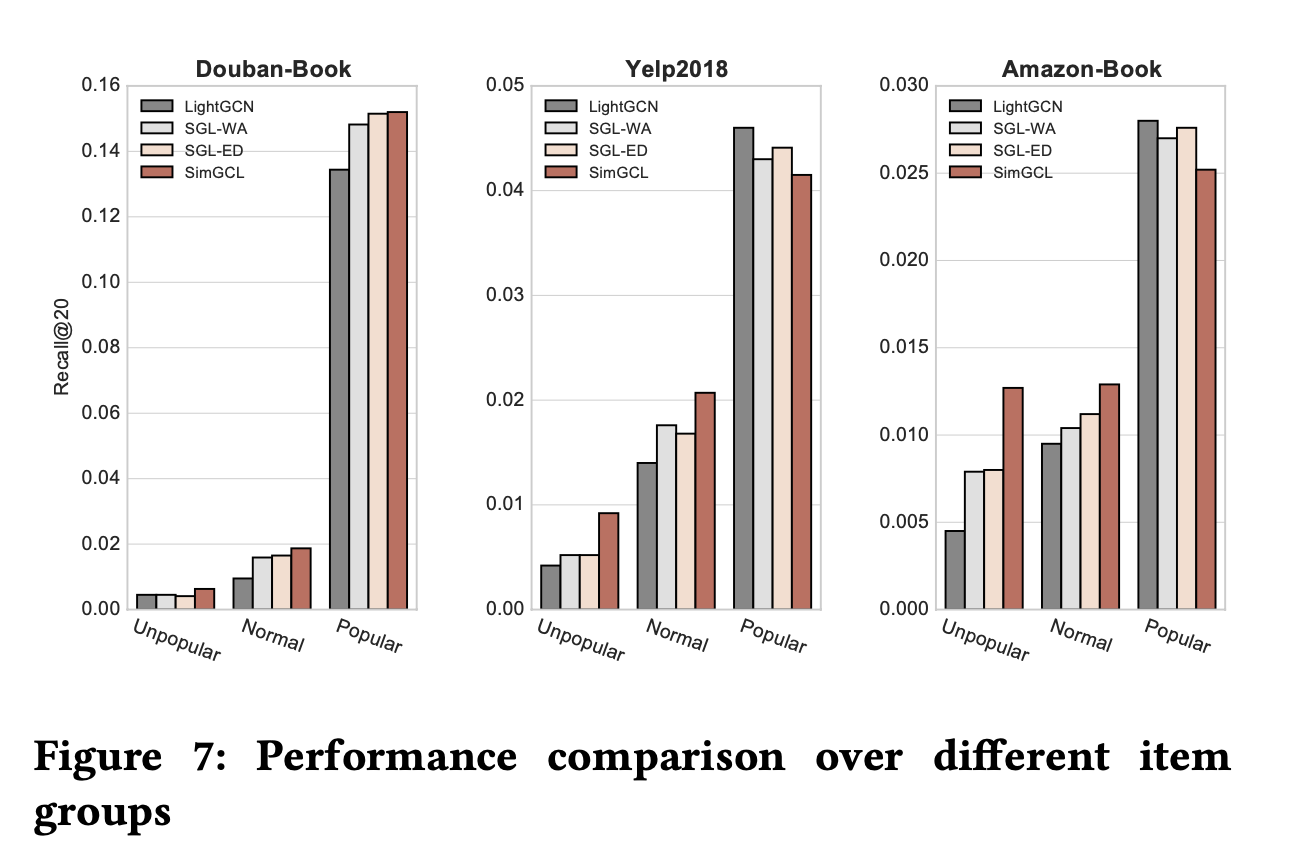
가장 적은 클릭/구매 수를 가진 80%의 아이템은 'Unpopular' 레이블로 지정하고,
가장 많이 클릭/구매 된 5%의 아이템은 'Popular' 레이블로 지정했으며, 나머지 아이템을 'Normal' 레이블로 지정했다고 한다.

결과적으로 SimGCL이 모든 데이터셋의 'Unpopular' 레이블 아이템에서 더 높은 정확도를 달성했음을 보인다.

Parameter Sensitivity Analysis

이 섹션에서는 SimGCL의 두 가지 하이퍼파라미터 𝜆와 𝜖의 영향을 조사한다.

𝜆의 영향

다음 그림은 𝜖를 0.1로 고정한 채로 𝜆의 변화에 따른 SimGCL의 성능을 보인다.

𝜆가 증가함에 따라 SimGCL의 성능이 처음에는 증가하다가 최고점에 도달한 이후에는 감소하기 시작함을 보인다.

𝜖의 영향

다음 그림은 𝜆의 영향을 조사하는 위 실험에 각 데이터셋의 성능 최고점을 기록한 𝜆를 고정한 후 𝜖의 변화에 따른 SimGCL의 성능을 보인다.

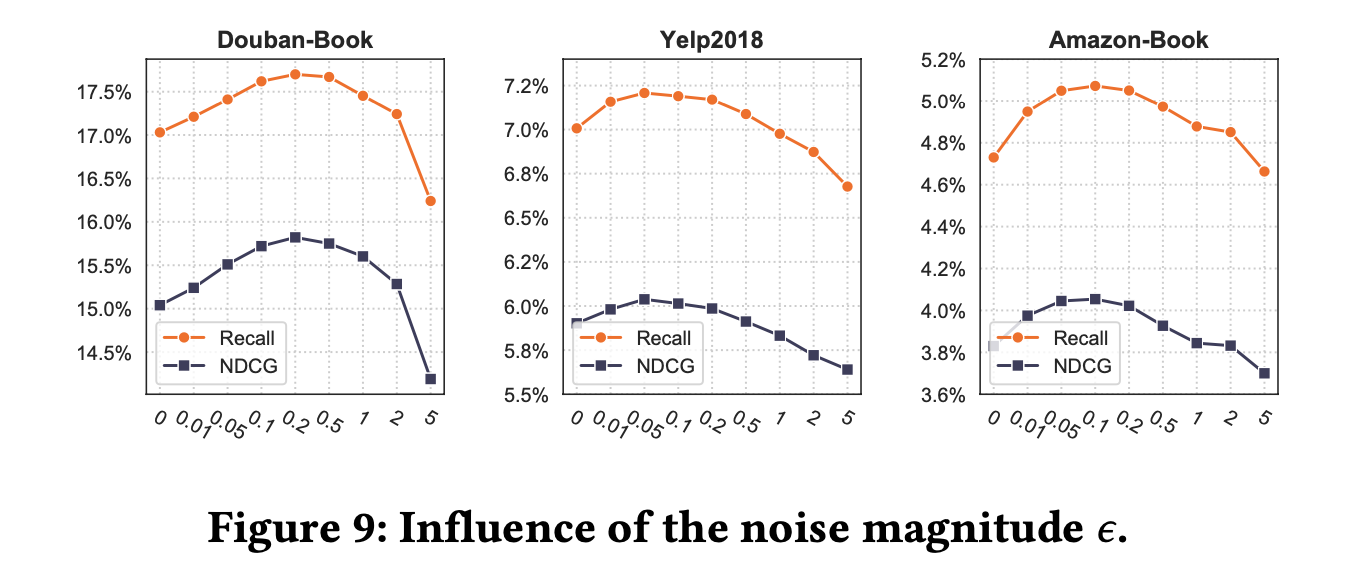
결과적으로 𝜖가 0.1 근처일 때 SimGCL이 최고의 성능을 보인다.

추가로 그림 9를 그림 8과 대조했을 때, 같은 범위에서 𝜖와 𝜆을 조절하면 그림 9에서 더 완만한 변화가 관찰되는것을 통해 𝜖가 𝜆를 조정할 때 보다 성능에 더 미세한 영향을 미침을 알 수 있다.

Performance Comparison with Other Methods

다음 표는 SimGCL의 역량을 확인하기 위해 데이터 증강 기반 SOTA 모델 네 가지와 성능을 비교한다.

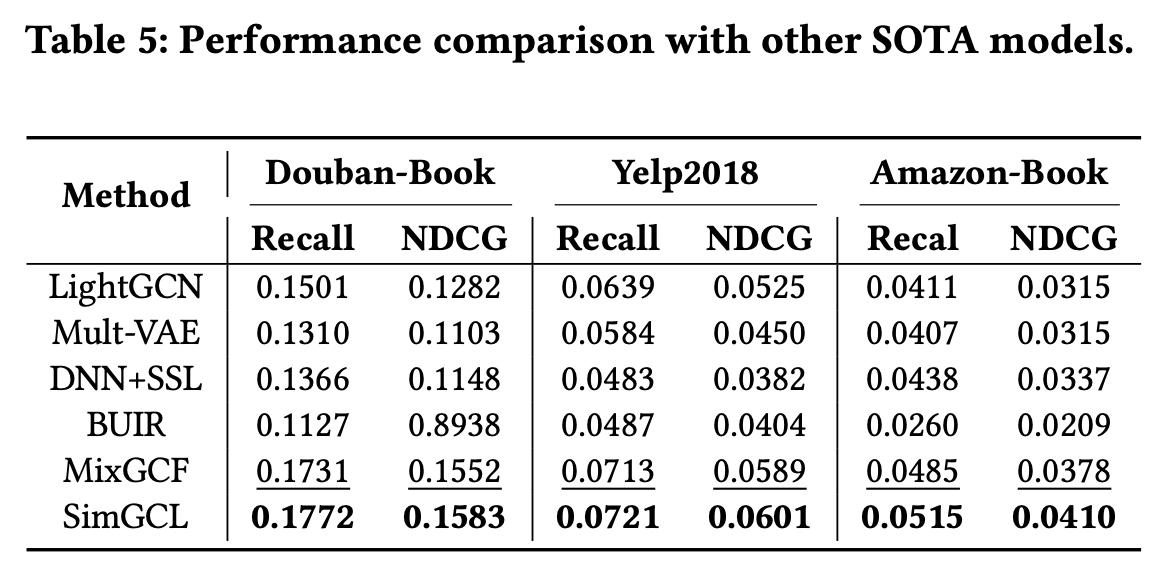
이를 통해 SimGCL이 최고의 성능을 보임을 확인할 수 있다.

Performance Comparison with Different Types of Noises

다음 표는 SimGCL의 데이터 증강에 균일 분포에서 샘플링한 무작위 노이즈 뿐만 아닌 가우시안 노이즈와 적대적 노이즈 같이 다른 종류의 노이즈에 대한 성능의 결과를 보인다.

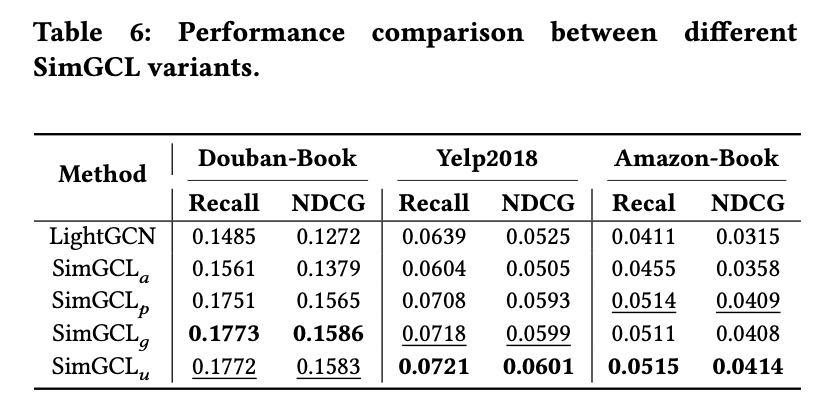
$p$는 노이즈의 두 번째 제약 조건을 만족하지 않는 균일 노이즈로 양의 분포 노이즈를 나타낸다.
$g$는 표준 가우시안 분포에서 생성된 가우시안 노이즈를 나타낸다.
$a$는 FGSM으로 생성된 적대적 노이즈를 나타낸다고 한다.

결과적으로 $SimGCL_g$는 $SimGCL_u$와 비슷한 성능을 보이는 반면 $SimGCL_a$는 아쉬운 성능을 보인다.
추가로 $SimGCL_p$의 비교적 성능이 약간 낮아지는 성능을 보이며, 이는 노이즈의 두 번째 제약 조건이 유효함을 나타낸다.

📖 CONCLUSION

본 논문은 기존 구조적인 그래프 증강법으로 알려진 노드/에지 드롭아웃에 비해 임베딩 수준에서의 증강법이 성능적으로 우수할 수 있음을 보임으로써 새로운 접근법을 선보이고, CL 기반 모델의 성능이 데이터 표현의 균일성과 연관이 있음을 실험적으로 입증한 의미있는 논문이라고 생각한다.

Reference

Are Graph Augmentations Necessary? Simple Graph Contrastive Learning for Recommendation