Machine_Learning5

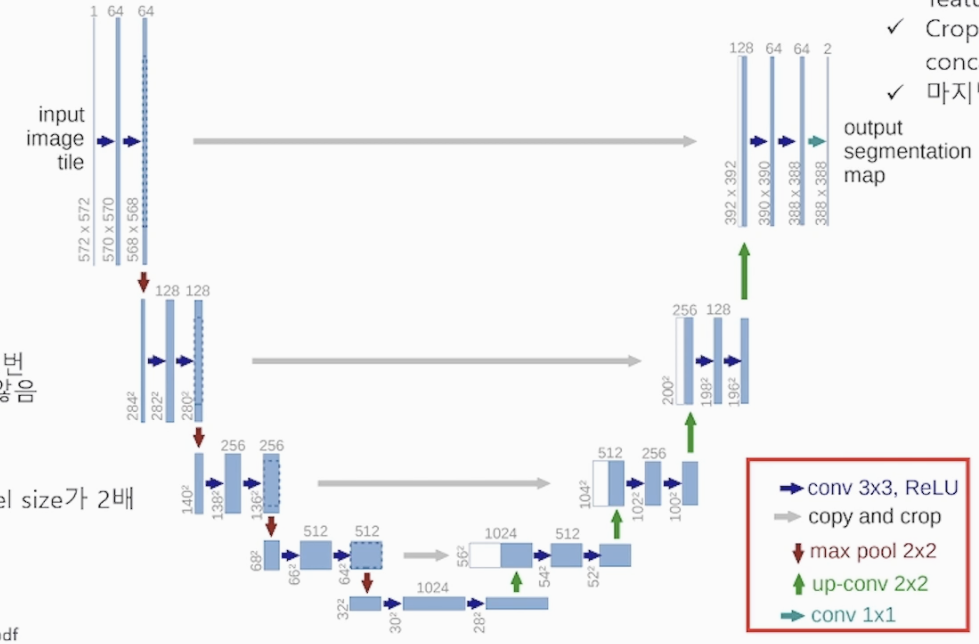
머신러닝 모델 (회귀)

회귀 모델이란?

• train data를 통해 학습하고, test data를 받았을 때, 이를 연속적인 숫자값으로 예측하는 것
  (여러개의 독립변수를 하나의 종속 변수에 대입하여 예측값을 찾는 것!)

목 차
1. 선형 회귀
(비선형 회귀는 선형 회귀에서 종속 변수(y)로 z(시그모이어 함수)를 구한다.z가 독립변수(x)의 계수와 관계없이 나오는 값이라 비선형 모델이라 합니다.)
2. 릿지 회귀
3. 라쏘 회귀
4. 엘라스틱넷 회귀
5. 랜덤포레스트 & xgboost
6. 하이퍼파라미터 튜닝
7. 평가(회귀)

• 머신러닝 구조 개념
  1) 데이터 셋
  2) 테스트 (예측값, 실제값 대입)
  3) 정확도 출력 (accruacy : : 분류는 매칭 정확도(확률), 회귀는 오차(error)값)
  4) 정확도 성능 Optimizing (하이퍼파라미터 조절)

  5) 검증
  (Validation: 모델이 test data 이전에 점검 과정, 검증 데이터 사용, 모의고사)
  (검증 방법 : KFold, Holdout, CV(교차검증), LOOCV)
  

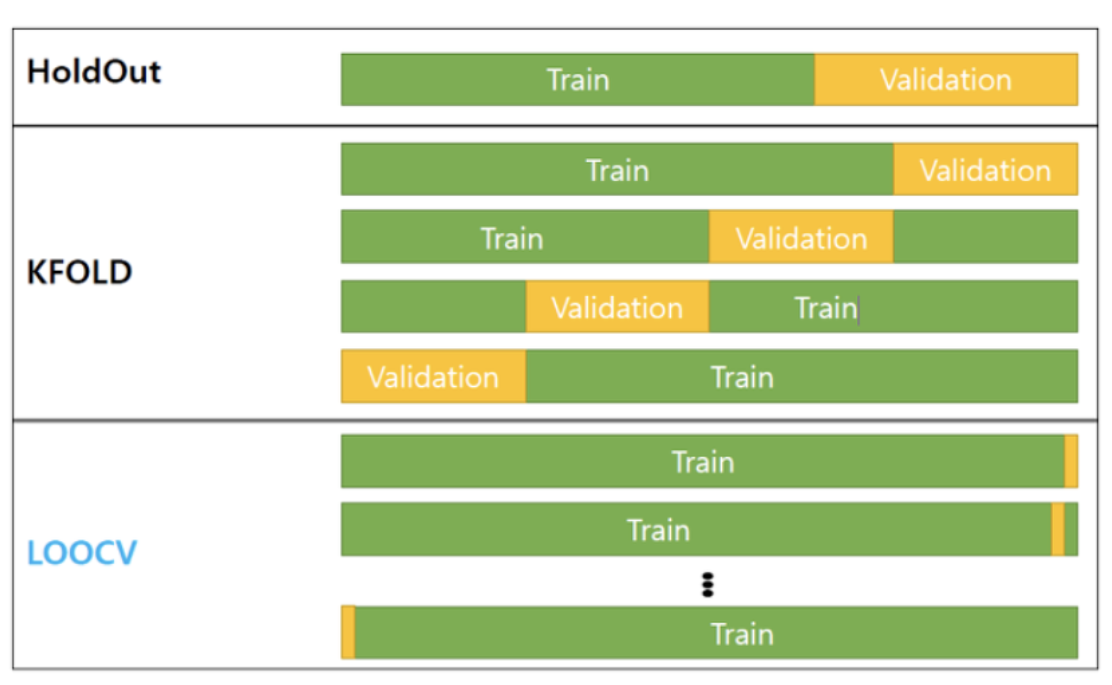
  6) 평가 (Evaluation: 실제값과 모델에 의한 예측된 값을 비교하여 차이(오차)를 구하는 과정)

• 기능 별 import 및 코드

	# 검증 데이터를 분리
	from sklearn.model_selection import train_test_split
    
    # 오차 제곱의 평균 구하기 (평가를 위함), mse
    from sklearn.metrics import mean_squared_error
    
    # 데이터 셋 로드 (당뇨병 : diabetes)
    from sklearn.datasets import load_diabetes
    
    # 선형 회귀 모델 import (LinearRegression)
    from sklearn.linear_model import LinearRegression
    
    # 릿지 회귀 모델 import (Ridge)
    from sklearn.linear_model import Ridge
    
    # 회귀 계수 
    model.coef_  # 피처(컬럼) 순서로 출력 된다
    
    # 회귀 계수 저장 (alpha = 뭐뭐 일때)
    coef['alpha뭐뭐'] = model.coef_
    
    # 데이터 프레임화
    pd.DataFrame(data=뭐뭐, columns=뭐뭐, columns=['뭐뭐'])
    
    # 엘라스틱넷 회귀 L1, L2 규제 비율 조절 (l1_ratio 60%)
    model = ElasticNet(alpha=0.0001, l1_ratio=0.6)
    
    # 하이퍼파라미터 튜닝
    # GridSearchCV, RandomizedSearchCV import 하기
    from sklearn.model_selection import GridSearchCv, RandomizedSearchCV
    
    # GridSearchCV 코드 (params 딕셔너리 작성했다고 가정)
    GridSearchCV(모델, 파라미터(params), cv=수, n_jobs=-1) #n_jobs=-1 코어 전부 사용
    grid.fit(x,y) # x,y 데이터 대입
    
    # 최적의 파리미터 찾기 (위 딕셔너리 params 중)
    grid.best_params_
    # 분류에서 정확도 찾기도 된다
    grid.bestscore_
    

1. 선형 회귀

• 선형회귀
  * 단순 선형 회귀 : 독립변수(피처) 1개
  • 다중 선형 회귀 : 독립변수(피처) 2개 이상
• 비용함수 (Cost funcitino)
  * 손실 함수(Loss function), 목적 함수(Objective function)
  • 오차(error)를 계산 (실제 값과 예측 값 차이)
  • 평균 제곱 오차를 최소화하는 파라미터를 찾음
• 경사하강법 (Gradient Descent)
  실제 값과 데이터 값의 거리 계산 방법 (오차 찾기)
  2차 함수 그래프에서 각 점 마다의 기울기 (0에 가까울수록 좋은 것)
  

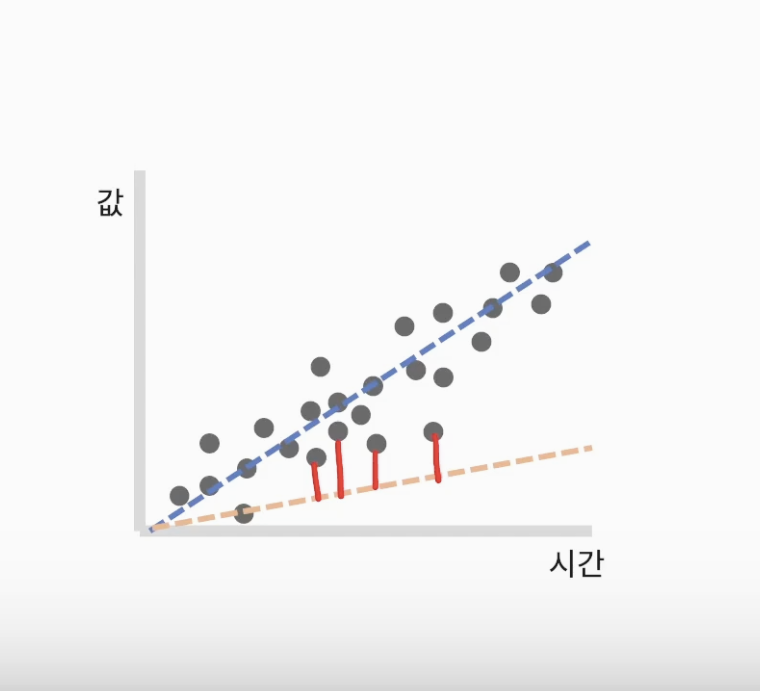
2. 릿지 회귀 (Ridge)

• 규제(regularization) 적용
  * 오버피팅이 되지 않기 위함
  • 규제 방식 : L2 규제
    (L1,L2 = 가중치 : input 데이터에 곱을 통해 비중을 실어주는 값)
    예시) 수능 ( 4~6월 점수 보다 7~10월 점수가 더 중요하다. 7~10월 점수에 비중을 더 준다)
  • 파라미터(alpha) 값을 활용해 조절 (alpha 값으로 모델 단순화/일반화, 가중치와 반비례)
  • alpha 값이 커질 수록 회귀 계수 값을 작게 만듦
    (회귀 계수 : 피처와 곱하는 계수, 피처 값에 영향을 준다)

3. 라쏘 회귀 (Lasso)

• 규제(regularization) 적용
  * 오버피팅 방지 위함
  • 규제 방식 : L1 규제
  • L2에 비해 회귀 계수를 급격히 감소시켜 0으로 만듦
  • L1 규제는 중요한 피처만 선택하는 특성이 있음

4. 엘라스틱넷 회귀

• 회귀를 위한 선형 모델
• L2 규제와 L1 규제를 결합한 회귀
• 출력 시간이 상대적으로 오래 걸림

5. 랜덤포레스트 & xgboost

• 튜닝을 통해 회귀 모델로도 사용 됩니다

6. 하이퍼파라미터 튜닝

• GridSearchCV, RandomizedSearchCV 활용
  1) GridSearchCV : 모든 경우의 수(하이퍼파라미터)를 탐색해서 튜닝
  2) RandomizedSearchCV : 내가 정한 random 수만큼 탐색

7. 평가(회귀)

• 평가 (회귀)
  1) MAE (meanAbsolute_error): 절대값 이용
  2) MSE (meansquarederror): 제곱 이용
  3) RMSE(root_mean_squered_error): 루트 이용, 루트 때문에 numpy 활용, 루트를 씌워서 오류값 크기를 줄이기 위함
  4) RMSLE(root_mean_squeredlog_error): 로그 이용, numpy,
  5) R2(RSquared_Score): 결정계수, 다른 것과 다르게 1의 가까울 수록 성능이 좋다
  (결정계수 : 회귀모델에서 독립 변수가 종속 변수를 얼마나 잘 설명해주는지의 지표, 상관계수의 제곱)