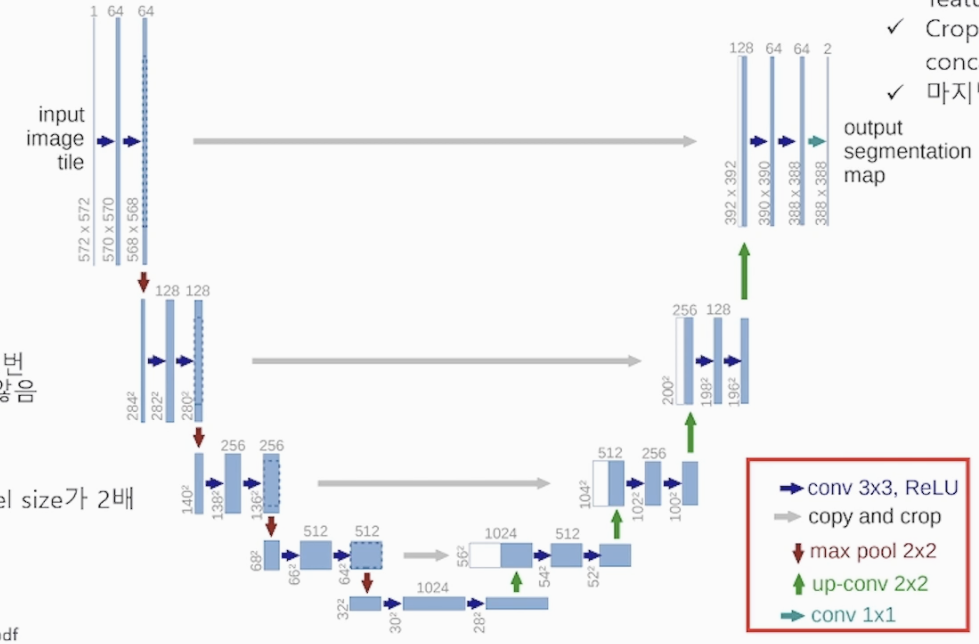
비지도 학습

• 지도 학습
  * 인공지능 모델에게 데이터로 정답을 알려주고, 잘 매칭 시키도록 학습 시키는 것
• 비지도 학습
  * AI 모델에게 정답을 주지 않고 스스로 데이터의 특징을 분류하여 그룹핑하고 매칭 시키도록 학습 시키는 것
  

• 목 차

1. 차원 축소 (PCA)
2. 군집 (클러스터링)

1. 차원 축소 (PCA 기법)

• PCA(Principal Component Analysis)
  1) 차원 축소 기법 중 대표적인 기법
  2) 고차원(피처가 많은)에서 저차원으로 축소하는 선형 투영 기법
  3) 데이터의 차원이 증가할 수록 거리가 증가하고, 오버피팅 가능성이 커짐

  가중치(weight) & 편향(bias) & 분산 (Variance)

  1) 가중치 : 입력값에 곱을 통해 비중을 실어주는 파라미터, 가중치가 클 수록 해당 피처는 모델에 더 많은 영향을 줌

  2) 편향 : 예측값과 정답(실제값)과의 거리,합을 통해 최종 출력값이 다양해진다(가중합), 뉴런의 활성화를 결정하는 파라미터
  (편향이 높다면 활성화 함수의 임계값을 넘기 어렵다. 뉴런 활성이 안되면 단순한 모델이 된다)

  3) 분산 : 예측값들의 밀집 정도
  (제곱과 절대값을 적용하는 이유 : 양수로 쌓기 위한 목적)

• PCA 단계
  1) 데이터에서 분산이 최대인 축을 찾음 (1축)
  2) 1축과 직교하면서 분산이 최대인 축을 찾음 (2축)
  3) 1,2축이 직교하고, 분산이 최대인 축을 찾음 (3축)

차원 축소 실습

• PCA(Principal Component Analysis) : 차원 축소 기법 중 대표적인 기법

	# 라이브러리 불러오기
	import pandas as pd
    
    # 와인 데이터 불러오기
   	from sklearn.datasets import load_wine
    dataset = load_wine()
    data = pd.DataFrame(datset.data, columns=dataset.feature_names)
    
    # 데이터 샘플 확인
    print(data.shape)	# 데이터 수와 피처 수 확인하기
    data.head()

스케일링 : PCA 전에 필요 작업, 범위를 재정의, 모든 피처들은 다른 단위와 크기를 가지고 있기 때문에 머신러닝 기법에서 문제가 생길 수 있다. (표준화 등)

	# StandardScaler 스케일링
    from sklearn.preprocessing import StansdardScaler
    scaler = StandardScaler()
    data = scaler.fit_transform(data)
    data[:3]		# 데이터 3개만 샘플 확인

	# 데이터 복사 (df 변수)
    df = data.copy()

PCA

	# PCA 라이브러리 호출
    from sklearn.decomposition import PCA
    
    # PCA
    pca = PCA(n_components=?)		# n_components 필수 ?는 차원의 수 & 피처(컬럼)의 수
    								# 실습은 2차원으로 진행
    # PCA 변환
    df = pca.fit_transform(df)
    
    # 데이터의 크기 확인
    df.shape
    >> (178, 2) : 178개의 데이터가 2개의 컬럼으로 축소 (array)

PCA(2차원) 시각화

	# 시각화 라이브러리
    import matplotlib.pyplot as plt
    
    # 데이터 프레임 변환
    df = pd.DataFrame(df)		# 현재 df는 numpy 형태(배열)의 type이라서 DF로 변환
    df.head()					# 테이블로 표현 확인
    
    # 시각화 (scatter)
    plt.scatter(df.iloc[:,0], df.iloc[:,1])		# x, y 축에 들어갈 데이터를 arg 로 대입
    											# x 는 df의 전체에서 첫번째 데이터, y는 2번째 데이터

	# scatter (c=target) : 그래프 상의 데이터가 색이 같아 구분이 안되어 실행
    plt.scatter(df.iloc[:,0], df.iloc[:,1], c=dataset.target)
    # 비지도 학습에는 target 값이 없다
    
    # 데이터 설명력 (%)
    print(pca.explained_variance_ratio_)
    print(pca.explained_variance_ratio_.sum())		# 2개의 피처를 합쳤을 때
    												# PCA 전후 차이 : 큰 차이 없음

PCA(3차원) 시각화 실습

	# 새 데이터 복사
    df = data.copy()
    
    # PCA (n_components=3)
    pca = PCA(n_components=3)
    
    # pca 변환
    df = pca.fit_transform(df)
    
    # data frame 변환
    df = pd.DataFrame(df)
    
    # 시각화(3차원)
    from mpl_toolkits.mplot3d import Axes3D		# 3차원 시각화를 위한 호출
    fig = plt.figure()							# 그래프 객체 생성
    ax = fig.add_subplot(111, projection='3d')	# Axes3d 축 fig 추가, 111은 서브플롯에 위치로 3자리 정수
    ax.scatter(df.iloc[:,0], df.iloc[:,1], df.iloc[:,2], c=dataset.target)
    

점진적 PCA

• 데이터 셋이 큰 경우 활용 (배치(batch)를 통해 점진적으로 수행)

	# 라이브러리 호출
    from sklearn.decomposition import IncrementalPCA
    
    # 데이터 복사
    df = data.copy()
    
    # 점진적 PCA 담기
    pca = IncrementalPCA(n_components=2, batch_size=16)		# batch 추가 (메모리 따라 다름)
    
    # 변환
    df = pca.fit_transform(df)
    
    # 시각화
    df = pd.DataFrame(df)
    plt.scatter(df.iloc[:,0], df.iloc[:,1], c=dataset.target)
    
    # 데이터 설명력 (%) : 상대적으로 설명력은 떨어지나 큰 데이터셋 사용시에는 유용하다 생각
    print(pca.explained_variance_ratio_.sum())

희소 PCA

• 적절한 희소성을 유지 (alpha값으로 조정)
• 오버피팅 방지

	# 라이브러리 호출
    from sklearn.decomposition import SparsePCA
    
    # 데이터 복사
    df = data.copy()
    
    # 희소 PCA
    pca = SparsePCA(n_components=2, alpha=0.01)
    
    # 변환
    df = pca.fit_transform(df)
    
    # 시각화
    df = pd.DataFrame(df)
    plt.scatter(df.iloc[:,0], df.iloc[:,1], c=dataset.target)
    

커널 PCA

• 비선형으로 차원 축소

	# 라이브러리 호출
    from sklearn.decomposition import KernelPCA
    
    # 데이터 복사
    df = data.copy()
    
    # 희소 PCA
    pca = KernelPCA(n_components=2)
    
    # 변환
    df = pca.fit_transform(df)
    
    # 시각화
    df = pd.DataFrame(df)
    plt.scatter(df.iloc[:,0], df.iloc[:,1], c=dataset.target)
    

SVD(Singular Value Decomposition) 특이값 분해

• 행렬을 특정한 구조로 분해하는 방식
  (무슨 특정 구조이려나? mxn 직사각행렬에서 A에서 벡터화 했을 때 직교하는 벡터를 찾는 구조, mxn 정방행렬에서는 고유값 분해를 한다)
• 신호 처리와 통계학 등의 분야에서 자주 사용됨

	# 라이브러리 호출
    from sklearn.decomposition import TruncatedSVD
    
    # 데이터 복사
    df = data.copy()
    
    # 희소 PCA
    SVD = TruncatedSVD(n_components=2)
    
    # 변환
    df = pca.fit_transform(df)
    
    # 시각화
    df = pd.DataFrame(df)
    plt.scatter(df.iloc[:,0], df.iloc[:,1], c=dataset.target)

2. 군집 (Clustering)

• 군집 분석은 유사성이 높은 대상의 집단을 분류하는 분석방법
• 계층적 군집 분석과 비계층적 군집 분석으로 구분함
  1) 전통적인 계층적 군집분석은 군집의 개수가 나중에 선정함
  2) 비계층적 군집분석의 KMeans는 군집의 수를 가장 먼저 선정함
  3) KMeans 군집분석은 초기 중심 값은 임의로 선정하며, 중심 값이 이동함
• 군집 분석의 평가 지표
  1) Silhouette(실루엣), Dunn Index 등 활용

군집 (Clustering)

비계층적 군집분석

• 대표적인 방법 KMeans
• K-평균군집(centroid), 임의의 지점 K개를 선택해 해당 중심에서 가까운 데이터를 군집화 하는 기법
• n_clusters 하이퍼파라미터 반드시 설정!

	# KMeans 라이브러리 호출
    from sklearn.cluster import KMeans
    
    # 데이터 불러오기
    from sklearn.datasets import load_wine
    dataset = load_wine()
    data = pd.DataFrame(dataset.data, columns=dataset.feature_names)
    df = data.copy()
    
    # KMeans 선언 및 학습
    kmeans = KMeans(n_clusters=3)		# 하이퍼파라미터 n_clusters= 군집 수
    kmeans.fit(df)
    
    # KMeans 예측
    pred = kmeans.predict(df)					# numpy array 형태, 피처 수 맞춰야함!
    
    # 실제값과 예측값 비교
    df['target'] = dataset.target
    df['pred'] = pred
    pd											# pred, target 컬럼 추가
												# target과 pred 아직 매칭 시키면 안됨!

PCA > 군집 > 시각화

	# PCA
    df = data.copy()
    pca = PCA(n_components=2)				# 2차원 축소
    df = pca.fit_transform(df)
    df = pd.DataFrame(df)					# numpy array형 데이터 프레임 화

	# KMeans : 군집화
    kmeans = KMeans(n_clusters=3)
    kmeans.fit(df)
    pred = kmeans.predict(df)
    df['kmeans'] = pred
    
    # 각 군집의 중심점
    centers = kmeans.cluster_centers_
    
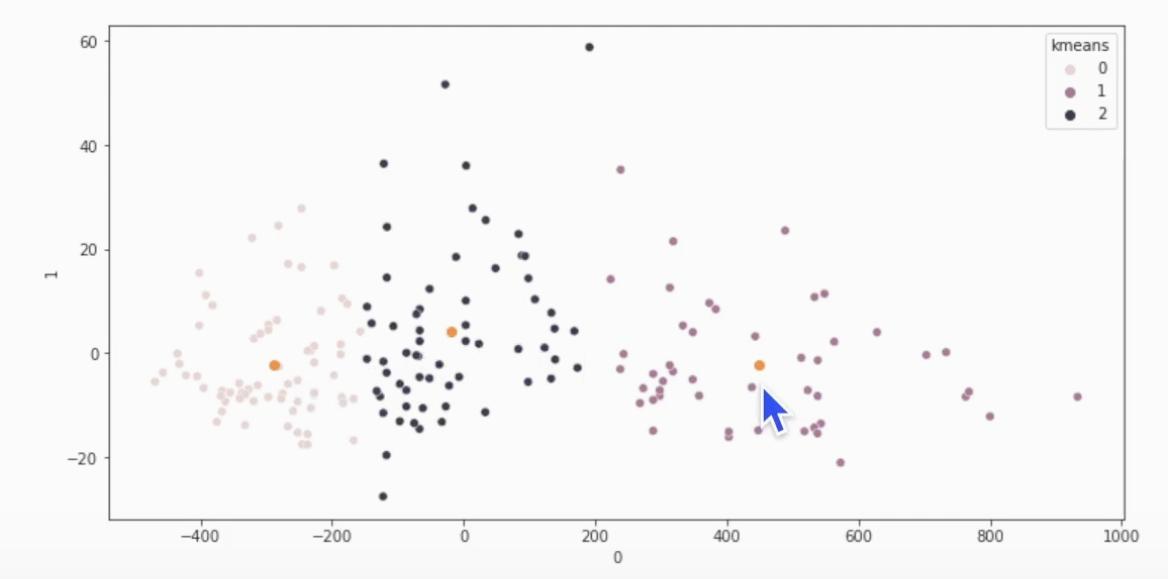
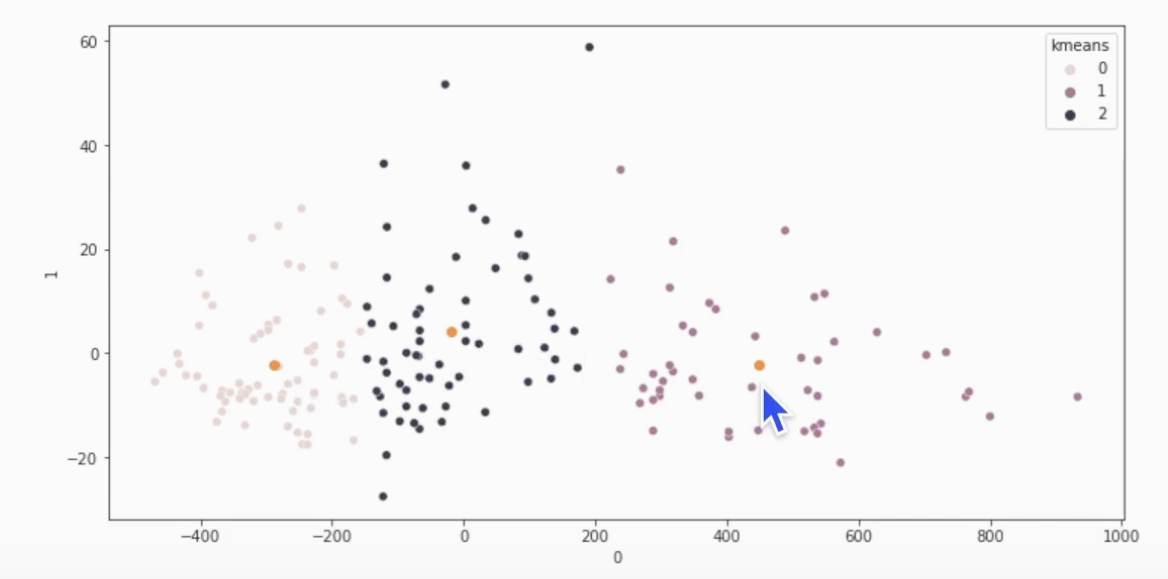
    # 시각화 (scatter)
    import seaborn as sns					# seaborn 라이브러리 호출
    plt.figure(figsize=(12,6)
    sns.scatterplot(x=df.iloc[:,0], y=df.iloc[:,1], hue=df['kmeans'])
    plt.scatter(centers[:,0], centers[:,1])	# 중심점 찍어보기 그럼 클러스트 값 == pred 값?

클러스트 개수 찾는 방법 (elbow method)

	# 군집 수 찾기 (시각화 > 그래프 경사가 완만해지는 점(분산이 적은 지점 찾기?)
    inertia = []
    for i in range(1,10)
    	kmeans = KMeans(n_clusters=i, random_state=2022)
    	kmeans.fit(df)
        inertia.append(kmeans.inneria_)
        
    plt.plot(range(1,10),inertia)		# 스코프만큼 시각화

계층적 군집분석

• KMeans와 달리 군집 개수를 사전에 설정하지 않음
• 덴드로그램

	# 덴드로그램
    from scipy.cluster.hieratchy import dendrograms, ward
    
    # PCA
    df = data.copy()
    pca = PCA(n_components=2)
    pca.fit_transform(df)
    df = pd.DataFrame(df)
    
    # 데이터 샘플링
    kdata = df[:3].copy()
    kdata = kdata.append(df[70:73])
    kdata = kdata.append(df[160:163])
    
    dataset.target[:3]			# 0 
    dataset.target[70:73]		# 1
    dataset.target[160:163]		# 2
    
    # 덴드로그램
    linkage = ward(kdata)		# ward 함수로 받아오기, 거리 정보 반환 받은 것
    dendrogram(linkage)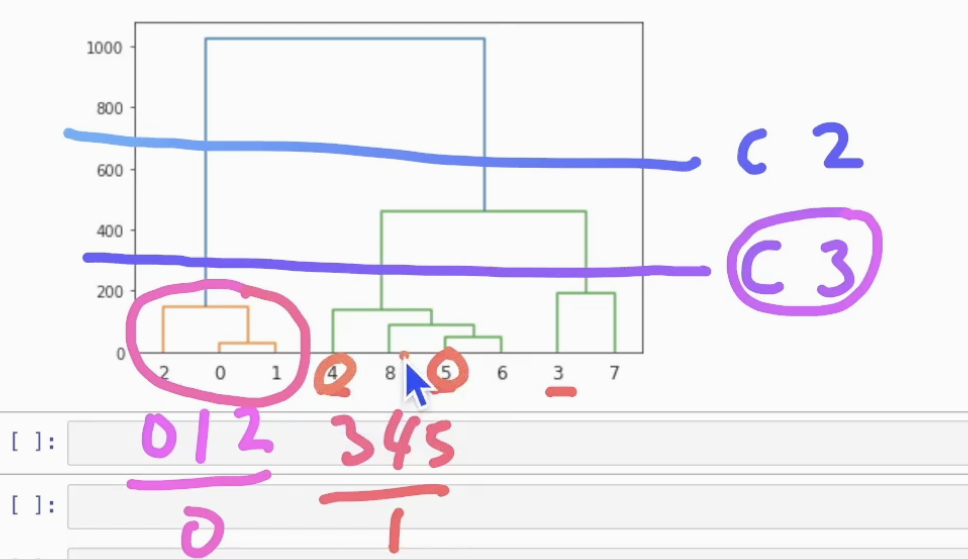

• target 1값은 pred 어떤 값과 매칭 되는지 확인

• print(df[df['target'] == 1]['pred'].mode().iloc[0]) (최빈값으로 제일 많이 매칭 된 값)

• 카운트 해보기

• df.groupby('kmeas').count()