범용적인 NPU 만들기(10) - 곱셈기(2) - 이론(2) - Modified Booth Algorithm

오늘은 중요한 알고리즘인 Modified Booth Algorithm(이하 MBA)에 대해 설명할 예정이다. 현재 설계하는 곱셈기는 MBA + Wallace tree 방식으로 설계할 예정이다. wallace tree에 대해서는 다음 포스팅에서 다루겠다.

---

간단하게 요약하면 MBA는 곱셈할 때 partial product의 수 (즉, row의 수)를 줄여서 곱셈을 간단하게 하는 방법이다. 이는 곱셈기의 성능, 면적 등에 크게 영향을 미치는데 그 이유는 다음과 같다.

일반적으로 곱셈은 2단계로 이루어지는데 바로 partial product 생성 -> partial product 덧셈이다.

여기서 첫단계인 partial product 생성은 오래 걸리지 않는다. 사람이 계산을 할 때도 각 partial product를 생성하는데는 오래 걸리지 않는데 특히 컴퓨터의 경우 완전히 병렬로 수행할 수 있기에 더욱 그렇다.

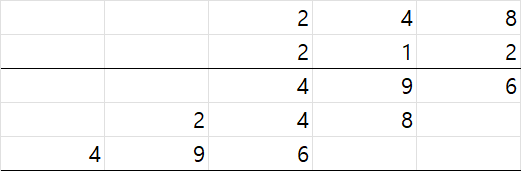
위의 그림은 3자리수 * 3자리수이지만 이게 늘어나 6자리수 * 6자리수가 되어도 partial product 생성의 딜레이는 달라지지 않는다. 차지하는 면적은 늘어나지만 애초에 각 bit당 하나면 충분하기에 전체 면적의 관점에서 보면 그렇게 큰 비중은 아니다.

하지만 두번째 단계인 덧셈에서는 자릿수에 따라 딜레이와 면적이 급격하게 늘어난다. 사람이 이를 수행할때도 먼저 가장 작은 자릿수끼리 더하고 carry out을 위로 올리고 다시 계산하고...하는 과정을 거쳐야해서 계산하는데 오래 걸리는데 이는 컴퓨터도 마찬가지다.

unsigned carry save multiplier를 예로 들면 n bit * n bit인 경우 row가 n개가 되고 면적은 대략 n^2 * Full adder, 딜레이는 2n * Full adder정도이다.

하지만 n bit * 2n bit로 row가 2배 늘어난 경우 면적은 2n^2, 딜레이는 3n이 된다. 결국 row의 수가 면적과 딜레이에 직결된다.

MBA는 이러한 중요한 영향을 미치는 row의 수를 줄이기 위한 알고리즘으로 이를 통해 회로의 면적과 딜레이를 줄일 수 있다.

---

MBA도 몇가지 종류가 있는데 이 포스팅은 radix-4 MBA를 기준으로 한다.

MBA는 간단한 공식을 기초로 하는데 바로

2k = 2k+1 - 2k = 2k+1 - 2 * 2k-1

이 공식을 이용한다.

결국 row의 개수 = multiplier의 자릿수 이기 때문에 이 공식을 이용해 multiplier의 자릿수를 줄여 row의 수를 줄인다.

기존의 multiplier가 1개 자릿값에 0 혹은 1이 들어갔다면 MBA에서는 위 공식을 이용해 -2, -1, 0, 1, 2 중의 하나가 들어간다.

이해를 돕기위해 한가지 예를 들어 MBA가 수행되는 과정을 보자.

위와 같은 곱셈을 수행한다고 하자. 여기서 위가 multiplicand, 아래가 multiplier가 된다.

아래의 multiplier를 위의 그림과 같이 겹쳐서 3비트씩 묶자.
마지막 주황색의 경우 2개 비트만이 남아 3비트씩 뭉치는게 불가능하므로 lsb 오른쪽에 0을 하나 더 붙여서 3개로 맞춰주자.

결과적으로 (1,0,1) (1,1,0) (0,1,0) (0,1,0) 이렇게 4개의 그룹이 형성된다.

이 각 그룹이 각 자릿값에 들어갈 숫자가 된다. 이를 구하는 공식은

그룹의 숫자가 (a, b, c)일 때 자릿값 X = -2a + b + c

이다. 이 공식은 위의 2k = 2(k+1) - 2 * 2k-1에서 유도할 수 있다.

위의 그룹들을 공식대로 숫자로 환산하면 (-1) (-1) (1) (1)이 되어 결과적으로 multipler (1 0 1 1 0 1 0 1)은

위와 같이 (0 -1 0 -1 0 1 0 1)로 변한다. 중간중간에 0이 들어가는 이유는 각 그룹이 나타내는 자릿수가 2bit씩 차이나기 때문에 공백인 부분에 0을 대신 넣은 것이다.

이제 이 둘이 같은 숫자인지를 비교해보자 본래 multiplier는

-128 * 1 + 32 * 1 + 16 * 1 + 4 * 1 + 1 /* 1 = -75

변형된 multiplier는

64 * -1 + 16 * -1 + 4 * 1 + 1 /* 1 = -75

으로 둘이 동일하다는 것을 알 수 있다.

일일이 공식을 대입해가서 풀어보면 공식이 맞다는 것을 알 수 있으나 번거로우므로 여기에 적진 않겠다.

---

위에서 multiplier을 변형해 곱셈에 적용하면 식이 이와 같이 변한다. (숫자의 밑줄은 실수로 넣은거다.)

중간 공백에 있는 0은 어차피 생략되니 굳이 넣지 않았다. 이에 따라 partial product는

이렇게 되어 row가 절반인 4개로 줄었다. 다만 이는 몇가지 생략된 그림인데 제대로 일반적인 경우에 대해 쓰면

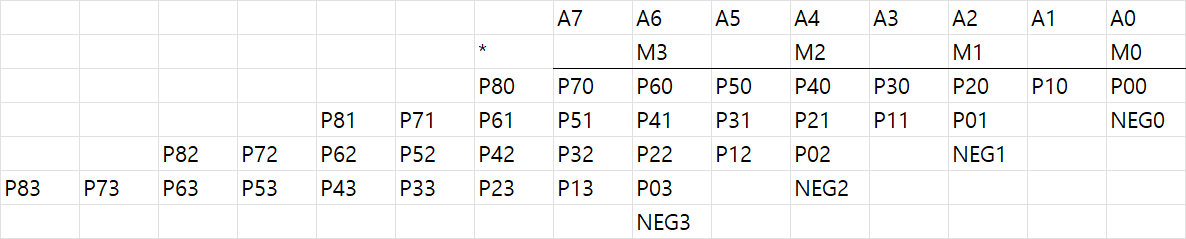
이렇게 된다.

row의 길이가 9비트로 변하고 neg라는게 추가된걸 알 수 있을텐데

이는 전자의 경우 각 자릿값에 들어갈 수 있는 숫자가 2 혹은 -2인 경우 1비트만큼 left shift 시켜 길이가 9비트로 늘어나기 때문이고

neg의 경우 자릿값이 -1 혹은 -2 일때 해당 row의 partial product를 1의 보수로 바꾸고 거기에 1까지 더해주어야 2의 보수가 되기 때문이다. 즉 neg는 자릿값이 -1 혹은 -2일때는 1, 아닐 때는 0이 된다.

당연히 이는 sign extension을 취하지 않은 형태인데 저번 포스팅에서 알 수 있듯이 그냥 sign extension을 그대로 하면 area가 낭비되므로 이를 알맞게 구성하면 이렇게 된다.

Sohiful Anuar Zainol Murad. Digital and Analogue Electronics Circuits and Systems. 1992, https://www.researchgate.net/figure/Sign-extension-prevention-method-15_fig3_290929092.

결과적으로 multiplier의 자릿수를 줄여 row의 개수를 줄일 수 있었고 이를 통해 area와 delay에서 이득을 볼 수 있다.