이전 포스팅을 작성한지 상당한 시간이 지났다. 지난 포스팅에서 processing core의 설계가 끝나 그동안 곱셈기에 대해 공부하고 아키텍처를 설계하고 있었다.
이전에 말했듯이 효율적인 곱셈기+덧셈기를 설계하는 것은 그 자체로 하나의 프로젝트라 할 수 있는 정도라 준비하는데 조금 시간이 걸렸다. 지금 어느 정도 설계가 끝나 우선 필요한 이론에 대한 포스팅을 올리려한다.
하드웨어 설계와 관련된 강의를 수강해본 사람은 그냥 곱셈기를 설계하는데 따로 필요한 이론이랄게 있나? full adder를 2차원으로 배열하면 되는데하는 의문이 들 수도 있다.
실제로 내가 수업 중에 설계했었던 unsigned carry save multiplier는 구조가 복잡할게 없다. 이론도 필요없다. 아주 간단하게 설계가능하다.
하지만 만들어야하는건 그냥 곱셈기가 아니라 효율적인 signed 곱셈기이기에 설계에 들어가기에 앞서 몇가지 배워야할 것들이 있다.
이번 포스팅에서는 먼저 signed 연산을 위해 알아야할 것들에 대해 다룰 것이다.
unsigned multiplication을 하던대로 signed 연산을 하면 오류가 생긴다. 이는 2가지를 고려하지 않았기 때문인데
첫째는 sign extension이고 둘째는 2의 보수법에서의 MSB의 표현값이다.
먼저 sign extension은 간단하다.
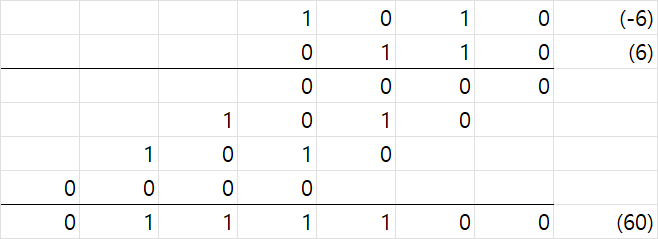
6*-6 = -36인데 60이 나왔다. 이는 partial product들을 sign extension을 하지 않아 음수가 양수로 바뀌었기 때문이다. sign extension을 한 경우
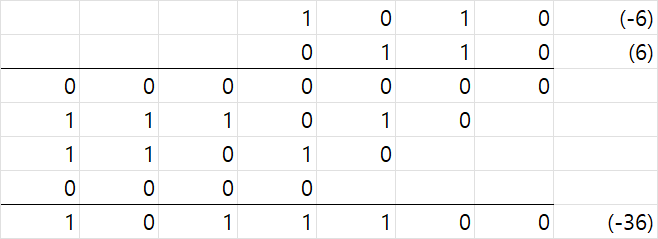
제대로 값이 나온다.
둘째로 2의 보수에서 MSB의 표현형이 문제라는건 이런걸 말한다.
abcd라는 이진법으로 표현된 숫자가 있다고하자. 이 이진수가 unsigned라고 가정한다면 값은 a * 2^3 + b * 2^2 + c * 2^1 + d * 2^0 이 된다.
하지만 2의 보수법으로 표현되었다고 하면 달라지는데 이때 값은
a * ( -(2^3)) + b * 2^2 + c * 2^1 + d * 2^0 이 된다.
결과적으로 MSB가 나타내는 값의 부호가 바뀐다는 뜻이다.
그래서 마지막 row의 partial product, 즉 mulplier의 MSB * multiplicand의 결과는 다른 row들과는 부호가 반대가 된다.
(왜냐하면 다른 row들은 2^k가 곱해질 때 마지막은 -2^k가 곱해지기 때문)
예를 들면 다음과 같다
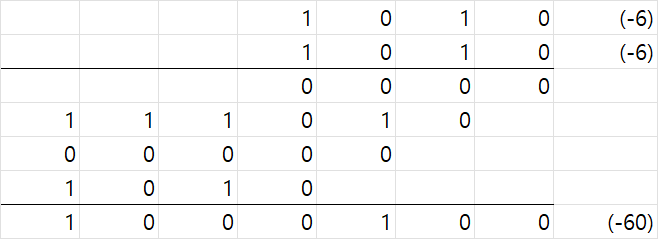
마지막 row에 -가 곱해지는 것을 고려하지 않았더니 -6*-6=-60으로 잘못된 값이 나온다.
하지만 마지막 row에 -을 곱해준다면 (즉 해당 row 대신 해당 row의 값의 2의 보수값을 넣는다면)
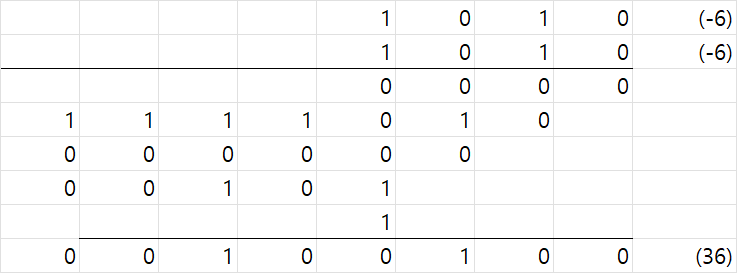
으로 제대로된 값이 나온다.
이제 이 2개를 알았으니 이거 고려해서 설계하면 끝이겠지싶겠지만 사실 그렇지 않다. 2개만 고려하면 된다해놓고 무슨 소린가 싶겠지만 정확히 말하자면 이 2가지만 고려하면 값은 제대로 나오는게 맞다.
하지만 있는 그대로 적용하면 회로가 면적을 불필요하게 많이 차지하게 된다.
예를 들어 carry save multiplier 형식으로 설계한다면
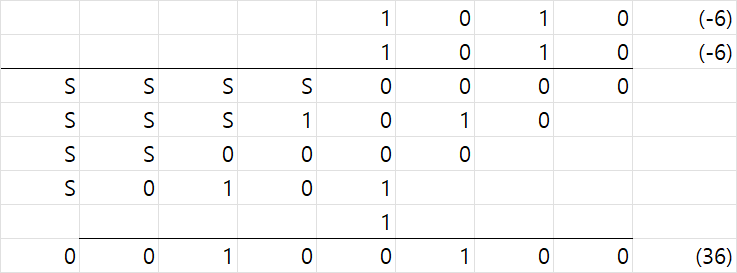
unsigned와 비교해서 sign extension을 위해 S 부분에 full adder나 half adder가 추가로 배치되어야하는데 이는 매우 비효율적이다. 오직 sign extenstion 기능만을 위해서 배치되는 adder의 수가 크게 증가해야한다.
이를 해결하기 위해서는 보다 적은 수의 모듈만을 가지고도 sign extenstion을 수행할 수 있게 계산 구조를 바꿔야하는데 이는 partial product의 각 bit들의 배치와 구성을 약간 수정하는 것으로 가능하다.
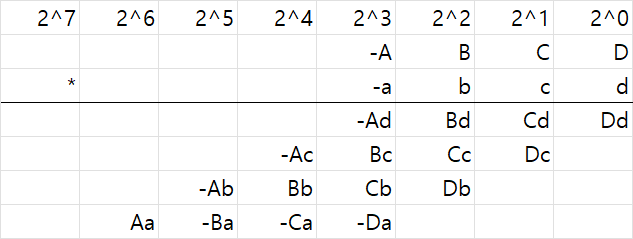
현재 각 partial product의 구성은 다음과 같이 되어 있다고 할 수 있다. 각 비트들이 분해되어 부호와 같이 표시되어 있으므로 따로 sign extension을 수행할 필요는 없다.
각 row의 MSB는 마이너스 값이고 반대로 마지막 row는 MSB만 플러스 값이다. 여기서 플러스 값끼리 마이너스 값끼리 모으고
빈칸 = 값이 없는 bit = 즉 0이므로 빈칸을 0으로 채워주자.
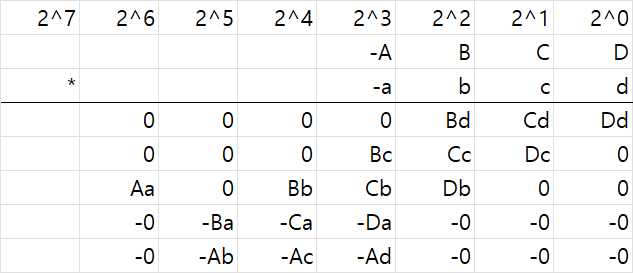
+0 = -0이므로 밑의 2 row는 0대신 -0으로 채웠다.
이제 각 row들을 다시 하나의 숫자로 결합하자. 즉 (0 0 0 0 Bd Cd Dd)가 1개의 숫자가 되고
(-0 -0 -Ba -Ca -Da -0 -0 -0)이 1개의 숫자가 된다. 그렇다하더라도 값은 변하지 않는다.
(-0 -0 -Ba -Ca -Da -0 -0 -0)을 -로 묶으면 -(0 0 Ba Ca Da 0 0 0)이 된다. 마이너스 부호는 결국 괄호 내부의 숫자의 2의 보수값을 구하라는 것과 같다.
부호를 없애 덧셈만으로 연산이 가능하도록 밑의 2 row의 마이너스를 계산, 즉 2의 보수를 대신 넣는다.
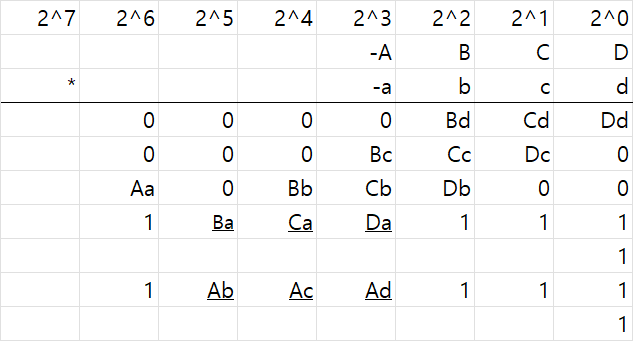
밑줄은 1의 보수를 뜻한다. 원래 윗줄로 표현하는데 엑셀에서 윗줄을 어떻게 표시하는지 몰라서 대신 밑줄로 표시했다. 그러니까 Ba = 0이면 밑줄친 Ba = 1이라는 뜻이다.
Ba나 Ca같은 bit들은 input에 달라지니 미리 연산할 수 없다. 0과 1만 미리 연산하자.
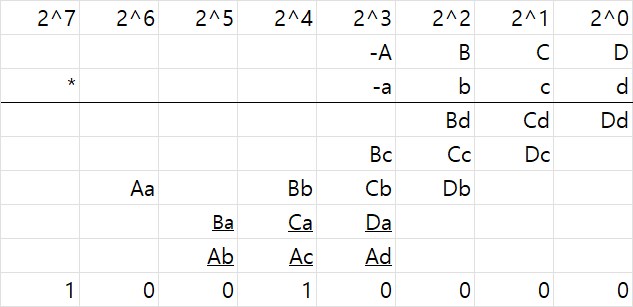
결과적으로 위와 같은 식으로 변한다. 총 5개의 row에 대해서 덧셈을 하면 된다. 물론 0은 계산할 필요가 없으니 최종적으로
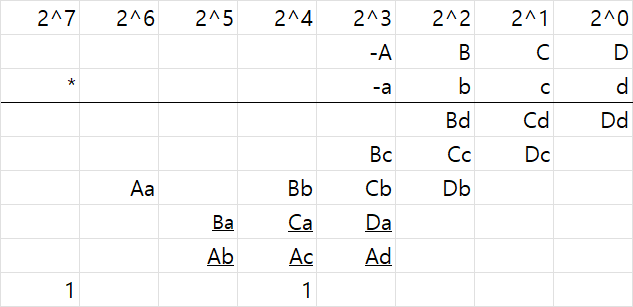
이렇게 된다. 결국 추가해야하는 adder의 개수가 크게 줄어든다.
한번 이렇게 계산해도 결과가 제대로 나오는지 확인해보자
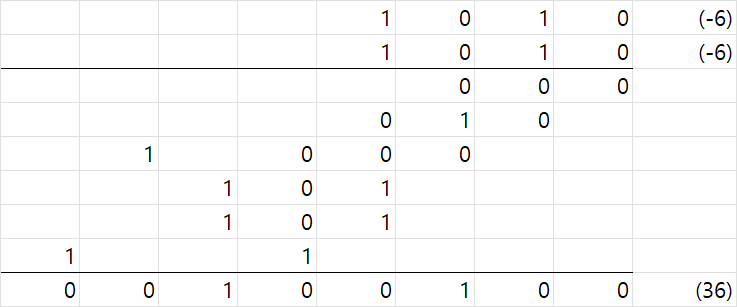
값이 제대로 나오는걸 확인할 수 있다.
큰 도움이 되었습니다, 감사합니다.