1. 코사인 유사도(Cosine Similarity)

코사인 유사도는 두 벡터 간의 코사인 각도를 이용하여 구할 수 있다.

$similarity=\cos{\theta}=\frac{A\cdot B}{\lVert A \rVert\lVert B \rVert}=\frac{\sum\nolimits_{i=1}^n A_i \times B_i}{\sqrt{\sum\nolimits_{i=1}^n (A_i)^2} \times \sqrt{\sum\nolimits_{i=1}^n (B_i)^2}}$

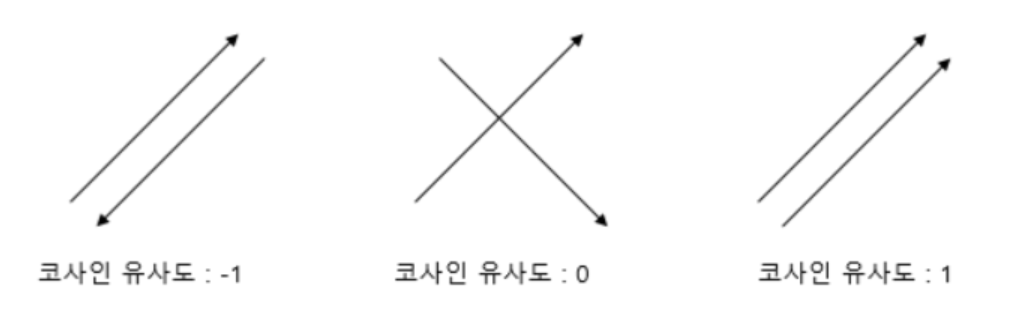
이에 대한 예시는 다음과 같다.
문서 1: 저는 사과 좋아요
문서 2: 저는 바나나 좋아요
문서 3: 저는 바나나 좋아요 저는 바나나 좋다요

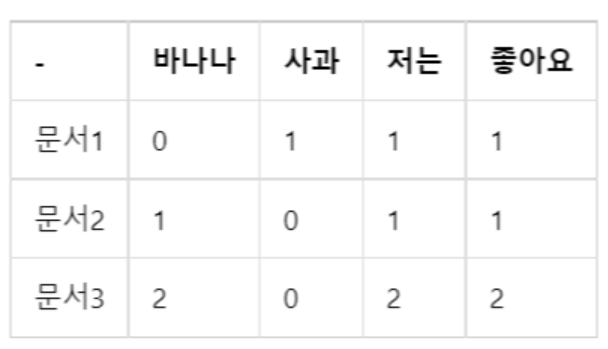
import numpy as np
from numpy import dot
from numpy.linalg import norm

def cos_sim(A, B):
	return dot(A, B)/(norm(A)*norm(B))
    
doc1 = np.array([0,1,1,1])
doc2 = np.array([1,0,1,1])
doc3 = np.array([2,0,2,2])

print('문서 1과 문서 2의 유사도 :', cos_sim(doc1, doc2))
print('문서 1과 문서 3의 유사도 :', cos_sim(doc1, doc2))
print('문서 2와 문서 3의 유사도 :', cos_sim(doc2, doc3))

문서 1과 문서 2의 유사도 : 0.67
문서 1과 문서 3의 유사도 : 0.67
문서 2과 문서 3의 유사도 : 1.00

2. 유클리드 거리(Euclidean distance)

다차원 공간에서 두 개의 점 $p$와 $q$가 각각 $p=(p_1,p_2,p_3, \dots, p_n)$과 $q=(q_1,q_2,q_3,\dots,q_n)$의 좌표를 가질 때 두 점 사이의 거리를 계산하는 유클리드 거리 공식은 다음과 같다.

$\sqrt{(q_1-p_1)^2+(q_2-p_2)^2+\dots+(q_n-p_n)^2}=\sqrt{\sum\nolimits_{i=1}^n (q_i-p_i)^2}$

이에 대한 예시는 다음과 같다.

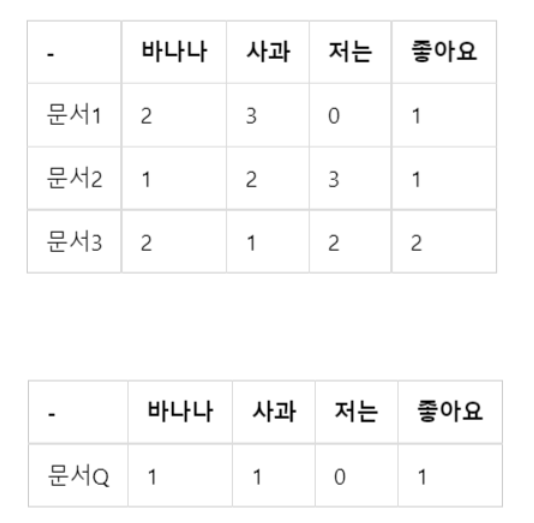
import numpy as np

def dist(x, y):
	return np.sqrt(np.sum((x-y)**2))
    
doc1 = np.array((2,3,0,1))
doc2 = np.array((1,2,3,1))
doc3 = np.array((2,1,2,2))
docQ = np.array((1,1,0,1))

print('문서1과 문서Q의 거리 :', dist(doc1, docQ))
print('문서2과 문서Q의 거리 :', dist(doc2, docQ))
print('문서3과 문서Q의 거리 :', dist(doc3, docQ))

문서1과 문서Q의 거리 : 2.23606797749979
문서2과 문서Q의 거리 : 3.1622776601683795
문서3과 문서Q의 거리 : 2.449489742783178

3. 자카드 유사도(Jaccard Similarity)

두 개의 집합에서 합집합에 대한 교집합의 비율을 나타낸 것이다. 0과 1 사이의 값을 가지며, 만약 두 집합이 동일하면 1, 공통 원소가 없다면 0이다.

$J(A,B)=\frac{\vert A\cap B \vert}{\vert A\cup B \vert}=\frac{\vert A\cap B \vert}{\vert A \vert + \vert B \vert - \vert A \cap B\vert}$

두 개의 비교할 문서를 각각 $doc_1, doc_2$라고 하면, 두 문서의 자카드 유사도는 다음과 같다.
$J(doc_1, doc_2)=\frac{doc_1 \cap doc_2}{doc_1 \cup doc_2}$

<참고 문헌>
유원준/안상준, 딥러닝을 이용한 자연어 처리 입문
https://wikidocs.net/21694
박호현 교수님, 인공지능, 중앙대학교 전자전기공학부, 2024